基于航向成形算法的船舶转向控制设计*

杨文辉 黄道平

(华南理工大学自动化科学与工程学院 广州 510640)

1 引言

图1 船舶转向操作

Job Van Amerongen在对船舶进行研究的时候,提出了船舶转向的理想操作[1],如图1所示。船舶转向操作分成三个阶段,0～t1:转向启动;t1～t2:转向保持;t2～t3:转向结束。不同使用者对船舶转向的共同要求:1)船舶的转向速度可以调节;2)船舶达到预定航向的时候,不会出现超调现象。

典型的船舶转向控制方法包括模型参考自适应控制,前馈加LQ控制器、模型跟踪器,以及基于Lyapunov稳定性理论的设计,在文献[2]提出了一种由低通滤波器、前馈控制器、反馈控制器组成的转向控制系统,并且按转向角的大小,分成三个不同的控制区域,分别进行控制。文献[3]扩展了文献[2]中对转向角分区控制的方法,将转向角度分成9个区域。这些控制器设计都有自己的优点。本文提出了一种航向成形算法,给定航向 ψd,经成形算法后变成理想转向参考信号ψr,并作为控制系统的参考航向与经低通滤波器之后的测量航向值之差Δ ψ作为控制器的输入信号。控制系统的设计,如图2所示。其中低通滤波器的作用是滤除高频波浪干扰的信号的影响。

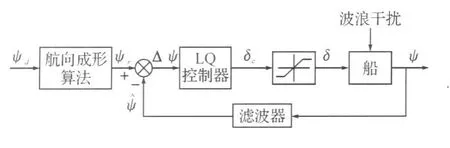
图2 船舶转向控制系统

2 船舶运动模型

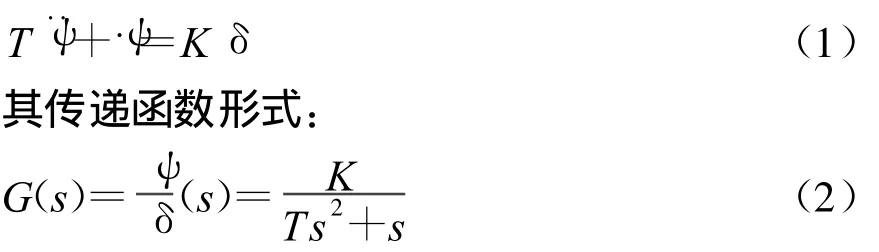
式(2)广泛应用于船舶自动舵的控制器设计中。求解该模型需要知道的8个船舶参数:航速V(m/s)、船舶两柱间长L(m)、船宽B(m)、满载吃水T(m)、船舶方形系数 Cb、排水量(m3)、船舶重心距中心距离 xC(m)、舵叶面积 Aδ(m2),具体计算可参考文献[4]。

在研究船舶的操纵运动时候一般只是考虑平面运动。日本学者野本谦作通过大量的实船试验,对船舶的航向控制运动方程进行了简化,得到低频范围内的舵角δ,到航向 ψ的一阶模型[4～5]:

3 航向成形算法

通过分析,可以发现,在船舶转向中,存在两种情况,情况1:如图3所示,可以将转向过程分成三个阶段,分别是一个加速、匀速、减速的过程。情况1多出现在转向角度较大的情况下。情况2:如图4所示,转向过程没有匀速阶段,这种情况多出现在转向角度小,且转向速度大时,例如在一些直航道上面的紧急调整航向。但并不否定转向角度小就不能出现情况1所述的三个转向过程,此时只要选择一个较小的转向速度仍然会出现情况1所述的过程。下面分别介绍两种情况下航向成形算法。

3.1 有三个转向阶段的航向成形算法

为了简化问题,假设情况1中出现的三个阶段分别是:0～t1:匀加速;t1～t2:匀速;t2～t3:匀减速,且加速和减速阶段的加速度a(°/s2)大小的相同,这样加速和减速过程就是对称的。当转向角度ψd,转向速度rd,由操作人员设定之后,就可以通过求解方程(3)～(5),得到时间 t1、t2、t3的值。

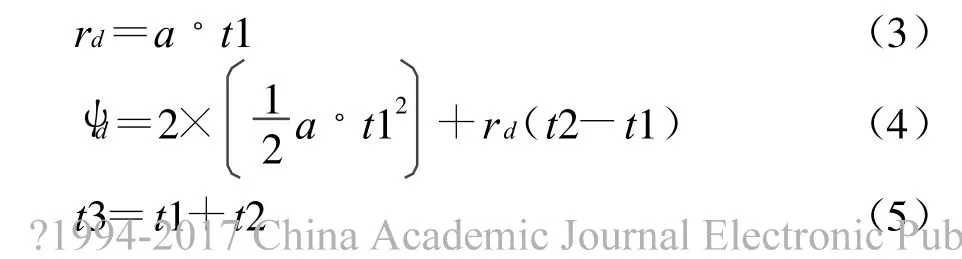
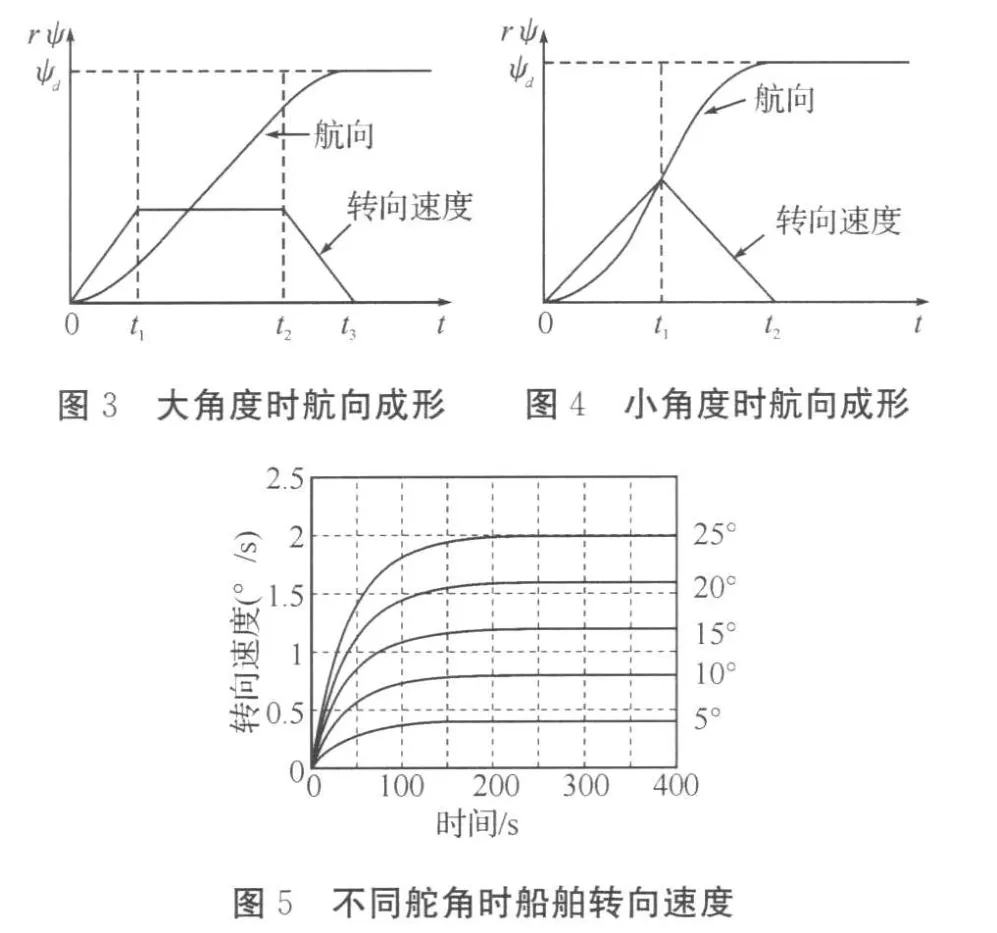
关于加速度a的取值,从图5中可以发现船舶转向的加速过程是一个加速度逐渐减小的变加速过程,如果直接根据这样的时间-速度关系来设计,则加速度a的值就会很小,考虑到船舶的大惯性特点,这里建议将a取在0.1附近,以加速船舶的转向启动。

关于转向速度r,在船舶转向中,其转向速率受到舵角的影响,就长时间来看,舵角与稳态的转向速度存在下面的关系:其中:ψ表示航向角,r表示船舶转向速率,K为野本模型中的增益系数,δ舵角。不同舵角下船舶转向速度,如图5所示。同时因为存在舵角限制,船舶的最大转向速度将由船舶允许的最大舵角决定,通常船舶最大舵角介于 25°～35°之间,当船舶的野本模型参数得到之后,就可以确定船舶的最大转向速率:

而且在实际船舶转向操作中发现,当转向角度大时,操作者希望使用较大的转向速度,以缩短转向的时间,此时舵机可能满舵,以达到较大的转向速度。当转向角度较小的时候,操作者希望使用较小的转向速度,以精确控制船舶达到设定航向。

从舵机使用的角度考虑,为了减少舵机的磨损,希望舵机能够平稳的操作,避免出现剧烈的操舵行为。从这个角度看,也是希望转向角度较小时,使用小的转向速度,以减少舵机的剧烈操作。基于这样的考虑,在非紧急情况下,可以下面的公式设定转向速度:其中:α速度系数,通过表1得到。当出现紧急情况的时候,可以直接设定转向速度为rmax。

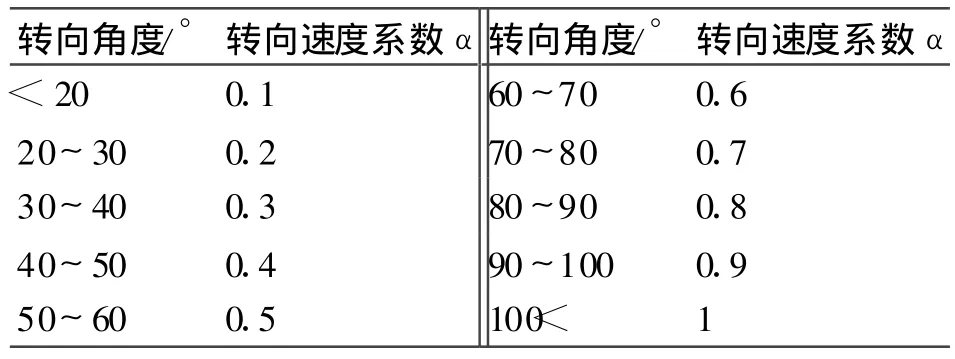
表1 转向速度系数表

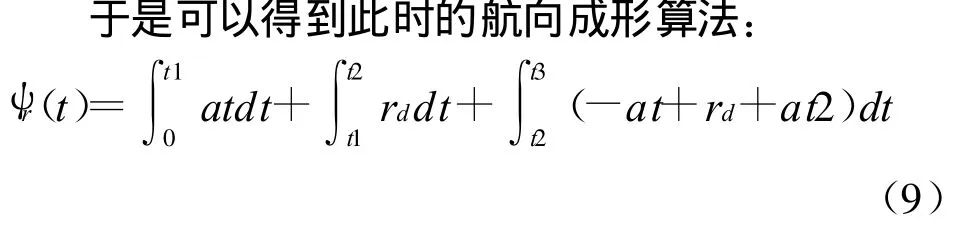
3.2 只有两个阶段的航向成形算法

情况2中的船舶转向过程只存在加速和减速的过程,假设:0～t1:匀加速;t1～t2:匀减速,且加速度a(°/s2)大小相同,当转向角度 ψd给定之后,就可以由式(10)、(11)计算得到时间t1、t2的值。

加速度a的取值,同情况1。此时的航向成形算法:

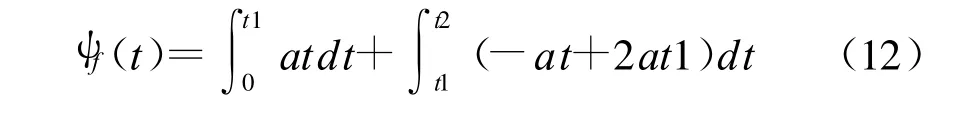
4 船舶转向控制器设计

基于闭环增益成形算法的鲁棒PID控制器[6],对于二阶对象:

其中:T1是根据系统的有效截止频率1/T1选择的时间常数。

5 滤波器设计

船舶难免会受到高频波浪干扰的作用,而这些干扰,会引起高频的操舵行为,所以在设计控制系统的时候,应该对测量的航向进行滤波,以排除高频波浪干扰的作用,减少舵机的磨损。通常波浪的频率介于0.05～0.2Hz之间[7],为此可以考虑设计一个低通滤波器。

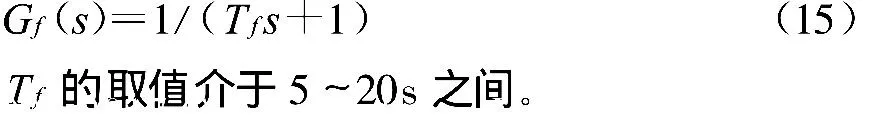
6 仿真研究

以5446TEU集装箱船COSCO Shanghai号[8]为仿真模型,船舶额定船速 U=24.5knots=12.6028m/s,其它参数如表2所示。

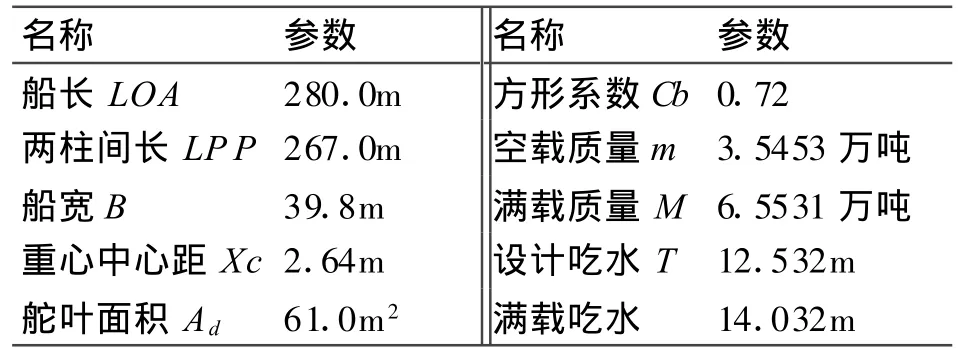
表2 5446TEU集装箱船Shanghai号

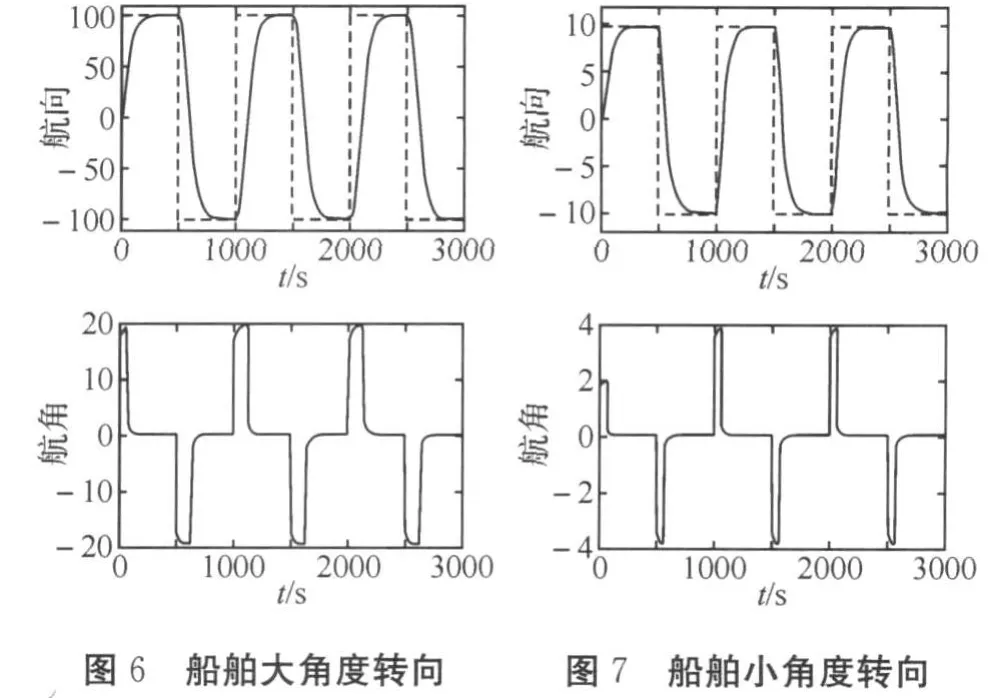
计算得到:K=0.0793,T=41.35(s),取Tf=10,T1=50,对船舶进行大角度转向和小角度转向仿真研究,结果如图6、7所示。从仿真结果可以看出,经过航向成形算法改进之后,船舶的转向平稳,没有出现超调,舵机的使用更加合理,转向角度大舵角大,转向角度小舵角小。

7 结语

本文基于理想船舶转向操作,设计的航向成形算法,其原理简单,易于实现,船舶转向过程更加的平稳,没有出现超调的现象,而且转向速度可以根据转向角度的大小或者用户要求进行选择,符合理想船舶转向要求。

[1]Van Amerongen,J.,Van Nauta Lemke,H.R.Criteria for optimum steering of ships[C]//Proceedings of Symposium on ship steering automatic control,Genoa,Italy,1980

[2]贾欣乐,蒋丹东,张显库.船舶转向控制器研究[J].大连海事大学学报,1998,24(1):23～28

[3]张显库,赵翔宇.船舶转向的鲁棒控制及其优化设计[J].哈尔滨工程大学学报,2006,27(3):319～322

[4]张显库,贾欣乐.船舶运动控制[M].北京:国防工业出版社,2006

[5]李殿璞.船舶运动与建模[M].哈尔滨:哈尔滨工程大学出版社,1999

[6]张显库,贾欣乐.求PID参数新方法[J].工程与电子技术,200,22(8):4～5

[7]Fossen,T.I.Guidance and Control of Ocean Vehicles[M].Chichester:John Wiley&Sons,1999

[8]徐黎黎.船舶运动智能控制及其虚拟仿真的研究[D].大连:大连海事大学硕士学位论文,2004