搜索论研究综述*

刘军伟 沙基昌 陈 超

(国防科技大学信C4ISR国防科技重点实验室 长沙 410073)

1 引言

搜索论是军事运筹学的一个分支,主要研究利用探测手段寻找指定目标优化方案的理论和方法。起源于二战期间,因盟国在大西洋的海上交通运输保障,受到德国潜艇的严重威胁,为了应对德国的潜艇,盟军组织人员运用数学的方法对德国的潜艇实施搜索,取得了很好的效果。Bernard O.Koopman三篇名为“搜索论”论文的发表,把二战期间研究搜索问题的基本理论作了介绍,搜索论正式作为一个研究内容被提出来。

二战之后搜索论的原理已成功应用于许多重要领域,从大洋深处搜索潜水目标到对外层空间的人造卫星进行监视、侦察。如1966年在西班牙帕洛玛附近的地中海海域搜索丢失的氢弹。之后搜索论被逐渐推广应用到了资源勘探(地下或海底矿藏资源及水中鱼群等资源),海空失事救援、航道搜扫,制导手段的探测目标等方面[1]。

本文从搜索理论、最优控制理论和对策论介绍了搜索论研究的内容,最后指出了目前搜索论研究的特点和存在的问题,给出了需要深入研究和完善的内容。

2 搜索理论

搜索理论是由和他的合作者在二战期间创建的。搜索理论的发展经历了四个时代[2]:经典时代、数学时代、算法时代和动态时代。经典时代(1942～1965)的主要代表是Koopman,他对静止目标的最优搜索问题即搜索资源的最优分配问题进行了研究,他在静止目标具有二元正态分布和探测函数具有指数函数形式的假定下研究了如何最大化发现目标的概率、并提出了在连续目标空间中且搜索资源连续可分的情况下进行搜索的资源分配方法[3～6]。在数学时代(1965～1975),主要是对最优搜索问题的数学本质进行研究,特别是静态目标的搜索问题,并开发了相关求解工具。主要成果是Stone的《最优搜索理论》(Optimal Search Theory),它是对文献[3～5]的完善和发展,解决了搜索问题的“最优搜索力配置存在的充分与必要条件”,研究的范畴仍然是对静止目标的搜索问题,初步涉及了对两种形式的动态目标的搜索,即“2单元格的马尔可夫型运动(Markov Type Motion)”和“有条件确定型运动(Conditionally deterministic motion)”。其主要思想是用拉格朗日乘法将搜索力型运动条件约束的最优搜索力配置模型转换为无约束条件的优化问题。1975～1985年被称为搜索理论的算法时代。随着相对廉价和高性能的计算机的普遍使用,这个时期的特点是人们将大量的研究精力转向致力于解决运动目标的搜索问题,把搜索理论的研究重心逐渐从数学和分析方面的求解转移到了从算法设计上去解决搜索问题。1985至今称为动态时代。主要的特点是在搜索过程中引入反馈机制,搜索过程中依据得到的信息及时更改搜索计划直到发现目标为止。

搜索理论由下面三个基本要素所构成:1)搜索目标,搜索是对搜索目标进行的搜索因此任何搜索问题均涉及到目标位置和移动路径的概率分布函数;2)探测函数,给出了将投入到某个区域的搜索资源的数量与搜索目标位于该区域时成功探测到该目标的可能性大小联系起来的函数关系;3)最优搜索计划,在搜索过程,根据目标的分布函数,对所拥有的有限的搜索力在一定成本约束下如何分配才能使发现目标的概率最大。最优搜索问题可分为静止目标搜索问题和运动目标搜索问题。下面分别对静态目标搜索问题和动态目标搜索问题进行综述。

2.1 静态目标搜索问题

静态目标搜索问题的研究成果是建立在Koopman,Dobbie,Gluss,De Guenin,Staroverov,Matula,Kadane,Onaga,Wegener,Chew,Mela,Tognetti,Weisinger等人的工作之上。Koopman最早提出了静态目标最优离散搜索模型,即Koopman模型。之后,De Guenin将Koopman模型推广到了连续空间中具有正规探测函数的搜索问题,给出了使得搜索函数达到最大值的正规探测函数须满足的必要条件。Staroverov研究了离散空间中具有正规探测函数的搜索问题。与前两者不同的是,Staroverov采用了使得查找和发现目标的时间期望值达到最小化的优化准则,而前两者采用的是使成功发现目标的概率最大化且总的搜索成本小于预算值作为优化准则。Mela通过采用初等方法进行论证,证明了探测搜索(Detection Search)的最优搜索策略和行踪搜索(Whereabouts Search)的最优搜索策略是不一样的。探测搜索是指在搜索资源成本的限定的情况下选择一种搜索策略使得找到目标的可能性最大;而行踪搜索是指在搜索资源成本一定的情况下判断目标最有可能出现的位置或区域。Chew研究了局部最优和全局最优搜索策略的关系,并被Kadane进一步推广。Kadane的研究结果包含在Neyman-Pearson定理中。

上述经典的静态目标最优搜索问题的主要结果都在基于已知目标的概率分布函数为假设前提的。朱清新研究了目标分布函数未知情况下的最优搜索问题。在此情况下的主要问题是如何选择一个好的目标分布函数,从而使得探测概率达到最大,并且需要计算非真实目标分布函数下设计搜索策略的误差。朱清新的研究考虑由最优搜索策略得到的探测概率的上下界,给出了在决策目标分布函数时的一些选择准则,并对搜索空间是两个单元格的情形做出误差估计,并将结果推广到N个单元格的情况[7～12]。

2.2 动态目标搜索问题

上世纪70年代中期到80年代中期,在军事需求实用化的推动下,搜索论进入了动态目标的搜索算法研究。到目前为止与研究动态目标的相关著作和论述可分为以下两类[12]:一类文章是讨论作某种特殊类型的运动的目标,并且这种运动目标的搜索问题可转化为用分析的方法去解决;另一类文章是基于1977年Brow n的观察报告的基础上,旨在建立针对动态目标的搜索问题的一般情况下的充分必要条件。在这些与动态目标有关的搜索问题的文献中,人们着重对两种特殊类型的运动目标进行了研究。第一类目标是有条件的确定动态目标,且具有可分解因子的雅可比行列式,这种类型的问题常常被简化为关于静态目标的一个等价问题,并最终可以用求解静态目标搜索问题的方法加以解决。第二类目标是作马尔可夫运动的目标。

按照目标是否对搜索者的行动做出反应来分,可把动态目标的搜索问题分为单边搜索(One-si-ded Search)和双边搜索(Two-sided Search)问题,有的文献也称为单向搜索和双向搜索。在单向搜索问题中,目标不能对搜索者的行为做出反应;与此相反,在双向搜索问题中目标能够对搜索者的行为做出反应。双边搜索问题有时也被称为搜索博弈(Search Games)问题。

2.2.1 单向搜索问题

单向搜索问题可以分为以下两种不同的类型:1)最优搜索密度问题;2)最优搜索路径问题。当搜索资源能够任意划分,并且在一定的时间和空间中的搜索资源的应用不会对其它时间和空间中的搜索资源的应用带来任务限制的问题就是最优搜索密度问题;而最优搜索路径问题是指在某个时间的搜索资源的配置对一个后续时间的搜索资源的配置施加某种约束。在搜索路径问题中,通常搜索者的运动速度和目标运动速度大致相同,如一艘潜艇搜索另一艘潜艇的情况;而最优搜索密度问题对搜索者的运动速度比目标的运动速度大得多的情况提供了一个合理的近似表达,如一架飞机搜索一艘在海上失事的船只的情况。

大多数用于计算动态目标的最优搜索方案的算法只适用于单向搜索问题。1)最优搜索密度问题算法。Brown应用Karush-Kuhn-Tucker条件设计出计算离散空间和时间中按照马尔可夫运动的目标的最优探测搜索资源的分配算法[13],他将运动目标的搜索问题转化为一系列的静止目标搜索问题加以解决。Stone在1975年提出了针对任意离散时间的运动目标和指数形式的探测函数的算法[14],之后又给出了关于正规探测函数的最优探测搜索问题的充分必要条件,允许用本质上可以是任意的随机过程去建立目标的运动模型[15]。并在1981年他与Discenza设计出计算生存者搜索问题的最优方案的算法[16],与Kadane设计计算运动目标的最优行踪搜索方案的算法[17]。Washburn提出了向前向后(forward and backward,FAB)搜索算法是对Brown的算法的推广,使Brown算法可应用于更广泛的一类支付函数,而不限于只适用于使得探测概率达到最大值的问题[18]。2)最优搜索路径问题算法。Trummel证明了离散时间和空间的最优搜索路径问题是一个NP完备性问题[19]。Ohsumi用一个扩散过程来描述目标的运动,探测函数用指数形式给出,用标准的最优随机控制理论的框架来解决连续时间和空间的搜索问题,从而得到一个动态规划方程(Hamilton-Jacobi-Bellman方程),满足这个议程的解决即可成为最优搜索方案的充分条件[20～21]。文献[22～23]也是应用最优控制理论解决最优搜索问题。文献[24]研究了目标在有限单元格进行马尔可夫型运动,搜索者的搜索路径受到限制的最优搜索问题,证明了最优搜索策略是固定的,并可由标准值迭代算法在有限的时间内计算出最优搜索策略。

此外,文献[25]用贝叶斯方法研究了单一自动传感器平台对丢失目标的最优搜索,以空中飞机搜索海面舰船或海面漂浮物为背景,以搜索平均时间和探测概率为指标研究了最优搜索的解。文献[26]研究了对随机隐蔽目标的最优搜索策略问题。

2.2.2 双向搜索问题

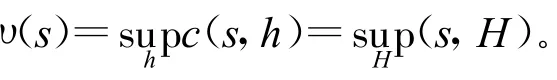
而对于多维连续空间的双向搜索问题,文献[29]得出以下结果,在二维或多维空间中,搜索者和规避者博弈问题的值υ满足υ=u/g,其中u是搜索空间的Lebesgue测度,g是探测速率。要使规避者被捕获时间大小(1-ε)u/g(规避者速度足够大的情况下),规避者要采用如下策略:随机选择一点Z1,并停留一段确定时间D,然后随机选择另一点Z2(独立于Z1),以最大速度移动到Z2,并停留时间D,如此反复。停留时间不应用太长,但另一方面,为了使在移动期间被捕获的概率较小,规避者也不应该太频繁地移动,即D不应用太短。多维空间中的搜索博弈问题的一个重要特性是存在一个以指数阶递减的函数P(t),使得对所有的t,在T时刻以后搜索者的捕获率约等0。

文献[30]主要针对已有的研究主要专注于双方本身的各种约束条件的分析,而忽略了结合搜索域中的各处探测概率进行分析。在Washbum的离散搜索模型基础上,提出了一种综合考虑搜索花费和探测概率的双边搜索模型,用以描述双方混策略的变化情况。

2.2.3 战术性博弈问题

战术性博弈问题是指研究与军事背景相关的动态目标搜索问题。文献[31]研究了潜艇与潜艇之间的追逐博弈。Baston在文献[32]研究了搜索者和规避者沿着直线运动的搜索问题。Dubins研究了类似的问题[33]。Danskin研究了带有声纳的直升飞机去探测一艘正在逃跑的潜艇的最优搜索策略[34]。Giammo[35]讨论了两支敌对军队在一个固定区域内互相搜索对方的问题。文献[36～37]研究了规避者间能够间歇性获取搜索者所在位置信息的搜索问题,这种间歇性获得信息的模型可用于海面上舰船通过声波定位搜索潜艇的情况。

3 最优控制理论

由于搜索问题与最优控制问题的相似性,人们已经尝试利用最优控制理论的结构框架去研究最优搜索问题,并取得一定成果。Ohsumi研究了探测一个做随机运动的目标的最优搜索问题,他用一个随机微分方程来描述目标的运动状态,把搜索问题作为最优控制问题来描述,并通过找到一个能最小化搜索者探测失败概率的控制信号来建立搜索者的策略[38]。他在文献[39]中给出了目标运动模型和搜索过程模型,最优搜索策略通过最小化成本泛函实现。他将最优搜索问题作为一个使得具有指数形式的成本泛函达到最小化的最优控制问题来描述,其中的成本泛函反映了发现目标的探测概率。在文中引入了搜索函数的函数并给出了它的时间进化情况,检验了搜索问题最优控制存在性的充分条件,提出了为实施最优搜索而必须解决的Cauchy问题和求解这个Cauchy问题的一种有效方法,即用于解一阶非线性微分方程的拟线性化技术,并给出了基于这种技术的两种仿真结果。Mangel在文献[40]中研究了只有一个搜索者的运动目标搜索问题。由于只涉及到常微分方程组,搜索密度函数 f(x,y,t,S)可通过渐进地求解密度函数所满足的搜索议程而近似地计算,并计算出了关于目标位置和不成功搜索的联合概率密度函数。

把最优搜索问题作为最优控制问题,利用动态规划原理,可推导用于解决作随机运动的目标的最优搜索问题的Hamilton-Jacobi-Bellman方程,可证明该方程的解就是所寻求的最优搜索策略,从而将原来的随机运动目标的最优搜索问题对应的随机系统最优控制问题转化为一个确定性系统中的两个等价问题,即解一个半线性二阶偏微分方程和求一个连续可微函数的最小值问题,为复杂运动和随机运动目标的最优搜索问题的解决开辟了一条新的途径。

4 对策论

文献[41]指出在军事领域的搜索与反搜索是一种具有冲突对抗性质的对策。这种对策具有以下主要特征:1)双方都在猜测对方可能会采取什么策略,从而以对方策略来决策自己的策略,即自己的策略是对方策略的反应;2)这种对策是一次性的,因此双方各自只能采取自己的纯策略;3)由于搜索与反搜索可能采取的策略中,它所要付出的代价或得到的利益,有时候是不易量化计算的,而且它的目标和结果主要在于采取一切可能手段去发现目标或不被发现,因此对抗结果的赢得,主要能表示出在所有可能的策略中采取什么策略对自己最有利,哪些对策结果出现对自己最好,或者说,双方各自最希望出现什么对策的结果,最不希望出现什么对策结果。这就是说,对策的赢得主要以双方各自对对策结果的选择序来表示。基于以上特征,文献[41]指出军事领域的搜索与反搜索是比一般对策更高层次的对策,提出利用元对策的原理、对抗分析方法去建立搜索与反搜索的元对策模型。

5 结语

从以上搜索问题的研究现状来看,到目前为止,对搜索问题的研究具有以下特点和问题:1)注重理论研究,离实际的应用还有一定差距,如Stone的《最优搜索理论》对静止目标搜索问题的研究在理论上达到了成熟状态,但是由于严格的假设条件、探测函数的正规性要求,使这些研究成果在现实的实用性受到了较大的限制。研究如何理论较好地应用到实际是搜索论形成的主要因素,也是以后在军事对抗中以及其他方面应用搜索论要解决的主要问题;2)研究角度大多者是从搜索者的角度建立搜索模型,如使得搜索者的成功搜索概率最大化,搜索者的搜索成本最小等,基于规避者的角度研究的文献相对不多。对基于规避者视角的规避搜索问题的研究是对搜索论内容的拓展;3)研究方法上,多数研究是把搜索问题作为一个决策问题来研究,即把某一方的策略固定后,再研究另一方的最优决策问题,这种研究方式简化了军事搜索问题的冲突对抗性,方便对搜索问题的研究,而且对搜索策略设计机制研究的文献也很少。文献[41]已经指出解决冲突对抗性质的对策问题的元对策方法,对我们的研究具有很好的借鉴意义,需要做进一步地深入研究。

[1]余滨,段采守.军事运筹学[M].长沙:国防科技大学出版社,2008

[2]L.D.Stone.What's happened in search theory since the 1975 lanchester prize?[J].Operations Research,1989,37:6

[3]B.O.Koopman.Search and Screening[R].Center for Naval Analysis,1956

[4]B.O.Koopman.The Theory of Search,part 1:Kinetic Bases[J].Operation Research,1956(4)

[5]B.O.Koopman.The Theory of Search,part 2:Target Detection[J].Operation Research,1956(4)

[6]B.O.Koopman.The Theory of Search,part 3:The Optimun Distribution of Searching Effort[J].Operation Research,1957(5)

[7]Q.Zhu,N.U.Ahmed.Second order Hamilton-Jacobi-Bellman Equations in Infinite Demensional Banach Space[J].Proceedings of Dynamic Systems adn Applications,1994(1):415～422

[8]Q.Zhu,N.U.Ahmed.Danamic Programming Equations of Stochastic Optimal Control n Banach Space[J].Stochastic Analysis and Applications,1995,13(3):369～387

[9]Q.Zhu,N.U.Ahmed.Some Results on Parabolic E-quation Associated with Stochastic Optimal Control[J].Nonlinear Analysis,Theory,Methods and Applications,1995,24(9):1305～1319

[10]Q.Zhu,J.Oommen.On The Optimal Search Problem:The Case when the Target Distribution is Unknown[J].Proceedings of the Chilean Computer Science Society,1997(11):268～277

[11]Q.Zhu,J.Oommen.Optimal Search with Non-regular detection functions[J].Journal of University of Electronic Science and Technology in Chendu,1999:125～128

[12]朱清新.离散和连续空间中的最优搜索理论[M].北京:科学出版社,2005

[13]S.S.Brown.Optimal Search for Moving Target in Discrete Time and Space[J].Operations Research,1980,28:1275～1289

[14]L.D.Stone.Theory of Optimal Search[M].New York:Academic Press,1975

[15]L.D.Stone.Necessary and Sufficient Conditions for Optiaml Search Plans for Moving Targets[J].Mathematics of Operations Research,1979(4):431～440

[16]J.H.Discenza,L.D.Stone.Optimal Survivor Search with Multiple States[J].Operations Research,1981,29:309～323

[17]L.D.Stone,J.B.Kadane.Optimal Whereabouts Search for a Moving Target[J].Operations Research,1981,29:1154～1166

[18]A.R.Washburn.Search for a Moving Target:The FAB Algorithm[J].Operations Research,1983,31:739～751

[19]K.E.Trummel,J.R.Kadane.The Complexity of the Optimal Search Path Problem[J].Operations Research,1986,34:324～327

[20]A.Ohsumi.Stochastic Control with Searching a Randomly Moving Target[C]//Proceedings:1984 American Control Conference,1984

[21]A.Ohsumi.Algorithms for Optimal Searching and Control Systems for a Markovian Target[J].Control and Dynamic Systems,1986:99～118

[22]M.Lukka.On the Optimal Searching Tracks for a Moving Target[J].SIAM Journal of Apllied Mathematics,1977,32:126～132

[23]M.Mangel.Search for a Randomly Moving Object[J].SIAM Journal of Apllied Mathematics,1981,40:327～338

[24]S.Singh,V.Krishnamurthy.The optimal search for a Markovian target when the search path is constrained:the infinite-horizon case[J].Automatic Control,IEEE Transactions on,2003,48(3):493～497

[25]F.Bourgault,T.Furukawa,H.F.Durrant-Whyte.Optimal Search for a Lost Target in a Bayesian World[J].Springer Tracts in Advanced Robotics,2006,24:209～222

[26]O.B nichou,M.Coppey,M.Moreau,et al.Optimal Search Strategies for Hidden Targets[J].Phys.Rev.Lett.,2005,94(19):4

[27]R.Isaacs.Defferenctial Games[M].New York:Willey,1965

[28]S.Gal.Search Games[M].New York:Academic Press,1980

[29]S.Gal.Search Games with Mobile and Immobile Hider[J].SIAM J.Control and Optimization,1979,17

[30]A LPER S,GAL S.Rendezvous search on the line with distinguishable players[J].SIAM Journal of Control and Optimization,1995,33(4):1270～1276

[31]陈俊,王令群,郑应平.基于离散模型的双边搜索博弈问题的研究[J].科技导报,2007,25(2):64～67

[32]A.Charnes,R.G.Schroeder.On Some Stochastic Tractical Antisubmarine Games[J].Naval Research Logistics Quarterly,1967,14:291～311

[33]V.J.Baston,F.A.Bostock.A High-Low Search Game on the Unit Interval[J].Mathematical Proceedings of the Cambridge Philosophy Society,1985,97:345～348

[34]L.Dubins.A Discrete Evasion Game[J].Annals of Mathematical Studies,1957,39:231～255

[35]J.M.Danskin.A HelicopterVerus Submarine Search Game[J].Operation Research,1968,16:509～517

[36]T.P.Giammo.On the Probability of Success in a Sudden Deach Search with International Moves Conflined to a Finete Area[J].SIAM Revies,1963,5:41～51

[37]S.P.Lalley,H.E.Robbins.Stochastic Search in a Conves Region[J].Probability Theory and Related Fields,1988,77:99～116

[38]M.Lehnerdt.On the structure of Discrete Sequential Search Problems and of their Solutions[J].Mathematis Operations and Statistic Series Optimization,1982,13:523～557

[39]A.Ohsumi.Optimal Searching for a Markovian Target and Relation to Optimal Stochastic Control[J].Theory and Applications of Nonlinear Control Systems,1986:569～583

[40]M.Mangel.Probabilit of Success in the Search for a Moving Target[J].Operations Research,1982,30:216～222

[41]张之駓.搜索论[M].大连:大连理工大学出版社,1992