小波变换在直升机高度表信号去噪中的应用*

2010-04-26袁汉钦

舰船电子工程 2010年4期

袁汉钦黄涛徐路

(海军驻景德镇地区航空军事代表室景德镇 333001)

1 引言

传统的直升机高度表采用FF T的算法来估计差频信号的瞬时频率,进而计算距离。这种方法在较低信噪比的情况下已经无法准确的定距。因此我们需要在FFT前滤出噪声的干扰,而采用FIR滤波器实现去噪的问题是:在不同的飞行条件下,目标信号频谱会有很大差异,为了兼顾各种极限飞行姿势,减少目标信号损失,不得不增大滤波器带宽,其后果必然是损失信噪比增益,而用差频信号探测目标的调频接收机对噪声的存在具有很高的敏感性,这就需要一种精度更高的去噪算法,鉴于此我们选择目前广泛应用的小波变换系数阈值去噪的方法对差频信号进行去噪处理[1]。

2 小波去噪原理及实现

小波阈值去噪法是一种非线性去噪方法,在最小均方误差意义下可达近似最优,并且可取得较好的视觉效果,因而得到了深入的研究和广泛的应用。其基本原理是:正交小波变换具有很强的去数据相关性,它能够使信号的能量在小波域集中在一些大的有限的系数中,而噪声的能量却分布于整个小波域内,因此,经小波分解后,信号的小波变换系数要大于噪声的小波变换系数,即可以认为幅值比较大的小波系数一般以信号为主,而幅值较小的系数在很大程度上是噪声。于是可以找到一个合适的阈值,小波系数大于阈值的认为其是由信号控制的,而小于阈值的小波系数则由噪声控制,从而可以对由噪声引起的小波系数进行萎缩来去除噪声[2]。

假设观察信号为

式(1)中,s(n)是有用的信号,u(n)是噪声序列。假定u(n)是零均值且服从高斯分布的随机序列,即服从 N:(0,)分布。对式(1)做小波变换,有

即两个信号和的小波变化等于各个信号小波变换的和。再令u(n)是零均值,独立同分布的平稳随机信号,记u=(u(0)u(1)…u(N-1))T,显然

式中,E{◦}代表求均值运算,Q是u的协方差对角矩阵。

令W是小波变换矩阵,对于正交小波变换,它是正交阵。分别令x和s是对应x(n)和s(n)的向量,向量X、S和U 分别是x(n)、s(n)和 u(n)的小波变换,即

由此,可得到一个重要的结论:平稳白噪声的正交小波变换仍然是平稳的白噪声。由该结论可知,对于式(1)的加性噪声模型,经正交小波变换后,最大程度的去除了s(n)的相关性,其能量将集中在少数的小波系数上。但是,噪声u(n)经正交小波变换后仍然是白噪声,因此,其小波系数仍然是互不相关的,他们将分布在各个尺度下的所有时间轴上。这一结论就为抑制噪声提供了理论依据,即在小波变换的各个尺度下保留那些模极大值点,将其他点置零,或是最大程度的减小,然后利用处理后的小波系数做小波反变换,即可达到抑制噪声的目的[3]。

去噪过程可以按以下方法进行处理:首先对信号进行小波分解,以三层分解为例(如图1),则噪声部分通常包含在 CD1、CD2、CD3中,再对分解以后的小波系数选取合适的阈值进行处理,然后用处理以后的小波系数重构信号,这样就可以达到去噪的目的。

图1 信号小波去噪的一般过程

1)小波分解。确定小波分解的层数 N,对信号进行N层小波分解。

2)小波分解高频系数的阈值量化。对第1到第N层的每一层高频系数,选择一个阈值进行阈值量化处理。

3)小波重构。根据小波分解的第N层的低频系数和经过量化处理后的第1层到第N层的高频系数,进行信号的小波重构。

在这三步中,关键的就是如何选取阈值和如何进行阈值的量化。阈值过高,则会将信号分量也当作噪声滤掉,丢失的信号信息太多;如果阈值太小,又会使得滤波效果不好,噪声的成分过多,不利于对信号的分析。从某种程度上来说,它直接关系到信号去噪的质量。

小波阈值萎缩去噪中,阈值函数体现了对超过和低于阈值的小波系数模的不同处理策略以及不同估计方法。设为原始小波系数,为估计小波系数,λ是阈值。

3 阈值函数的选取

1)常用的阈值函数:

(1)硬阈值

当小波系数的绝对值小于给定的阈值时,令其为零;而大于阈值时,则令其保持不变,即

(2)软阈值

当小波系数的绝对值小于给定的阈值时,令其为零;大于阈值时,令其都减去阈值,即

2)改进的几种阈值函数

硬阈值和软阈值方法虽然在实际中得到广泛的应用,也取得了较好效果,但该方法本身存在一些潜在的缺陷。在硬阈值方法中,在λ和-λ处是不连续的,利用重构所得的信号可能会出现振铃、伪吉布斯效应等失真。由于软阈值方法估计出来的虽然整体连续性好,会使去噪效果相对平滑得多,但是当||≥λ时与ωj,k总存在恒定的偏差,直接影响重构信号与真实信号的逼近程度,势必会给重构信号带来不可避免的误差;此外,软阈值函数的导数不连续,而在实际应用中经常要对一阶导数进行处理,所以软阈值函数具有一定的局限性。鉴于此,我们需要对经典的软、硬阈值函数进行改进,构造出更好的阈值函数[4]。常见的几种改进方案有:

特别地,当α分别是0和1时,上式即成为硬阈值和软阈值估计方法。对于一般的0≤α≤1来讲,该方法估计出来的数据的大小介于软、硬阈值方法之间,故称之为软、硬阈值折中法。

该方法的思路很简单,也很通俗,但其去噪效果很好。由于单纯的软阈值方法估计出来的,在||≥λ时,其绝对值总比 ωj,k要小,因此要设法减小此偏差;但若把这种偏差减小为零(硬阈值情况)也未必是最好的,因为 ωj,k本身就是由uj,k和vj,k组成的,它可能由于 vj,k的影响而使|ωj,k|＞|uj,k|(对于大多数的ωj,k来讲),而我们的目的是使‖-uj,k‖尽可能小,因此,令||的取值介于|ωj,k|-λ与|ωj,k|之间可能会使估计出来的小波系数更接近于uj,k。基于这一思想,我们在阈值估计中加入α因子,在0与1之间适当调整α的大小,可以获得更好的去噪效果[5]。

(2)模平方处理法

先考虑ωj,k＞0的情形,然后把结论推广到 ωj,k＜0的情况。在软阈值估计方法中,当ωj,k＞0时,式(8)等价于

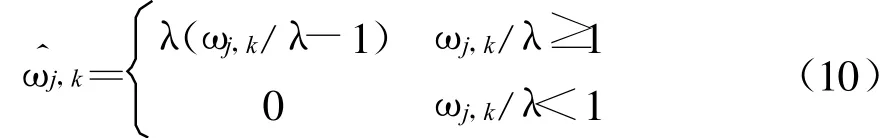
如果把ωj,k/λ看成一个整体,则式(10)的实际含义为:当 ωj,k/λ≥1时,ωj,k被认为主要是由信号所对应的小波系数,予以保留;否则,ωj,k被认为主要是由噪声引起的,应当消除。该模型虽然与软阈值模型完全等价的,但可以从中得到一些启示,比如,可以取

即先对ωj,k/λ进行平方处理,使得每一个系数与1的偏离程度增大,这样可以促使信噪分离,然后再对其做软阈值处理,最后平方得到。

以上讨论的是 ωj,k＞0时的情形,对于一般情况,有

(3)指数型阈值函数

其中N为任意正常数。

指数型阈值函数不但同软阈值函数一样具有连续性,而且当|ωj,k|≥λ时是高阶可导的,便于进行各种数学处理。指数型阈值函数以=ωj,k为渐近线 ,随着 ωj,k的增大逐渐接近 ωj,k,克服了软阈值函数中与ωj,k之间存在恒定偏差的缺点。当 N→∞时,式(14)为软阈值函数;当 N →0时,式(14)为硬阙值函数。可见,指数型阈值函数是介于软、硬阈值函数之间的一个灵活选择,可以通过 N的取值变化,得到使用有效的阈值函数[6]。

4 仿真实验

为了实现小波变换在对差频信号进行去噪声方面的应用,本文在MATLAB7.1环境下进行了仿真实验。假设信号为信噪比10dB的差频信号,截取的信号时间为4s,采样点为4000个点,采用的小波基为sym4小波,分解层数为4层,阈值λ采用每个尺度可变的 δ(2logN)1/2/log(j+1),其中,j为分解尺度,N为信号长度,各种消噪方法得到的信噪比和均方根误差如表1所示。

软、硬阈值折中法、模平方处理法等三种改进的阈值处理法去噪的效果都要明显好于传统的软、硬阈值法。其中,模平方处理法略胜于软、硬阈值折中法;指数型阈值法的去噪效果较上述几种方法都要好[7]。

如图7所示,我们对信噪比为0dB、规则区频率为3Hz的差频信号作FFT,得到了它的频谱,我们可以看到信号的谱线已经湮没在噪声谱线中了,对去噪后的差频信号进行FFT,得到如图8所示频谱,从图中我们可以看出能较准确的测出差频信号的瞬时频率[8]。