基于有限元的新型超声内圆磨削系统特性研究

殷 振 李 华 李 艳 谢 鸥 章志伟

（①苏州科技学院机电工程系，江苏 苏州 215009；②苏州高博软件技术职业学院基础部，江苏 苏州 215163；③河南工业大学机电工程学院，河南 郑州 450007）

超声振动内圆磨削是一种全新的超声复合振动加工技术，采用超声振动内圆磨削加工时磨削力小，发热少，工具磨损小，可以有效地解决砂轮堵塞、磨削烧伤等问题［1］，在超声振动内圆磨削加工过程中，相邻磨粒的磨削路径随机干涉程度增加，从而改善了被加工表面的网纹结构，进而可以提高磨削加工质量、加工精度和加工效率。

在以往的超声振动内圆磨削系统设计过程中，振子（由换能器、变幅杆和工具构成）、套筒、外套均分别设计，存在振子整体谐振修正工作量大、整体谐振困难、套筒表面受振子影响存在微小振动，以致影响主轴回转精度和轴承寿命等问题，且从超声波发生器到换能器的碳刷、集流环电信号传输方式存在碳刷、集流环滑动磨损较快、裸露导线、转速不宜过高等缺陷。在新型超声振动内圆磨削系统的设计中，采用有限元整体分析的方法优化系统结构，并应用新型的旋转式非接触电信号传输装置有效地解决了上述问题。

1 新型超声振动内圆磨削系统的有限元分析

如图1 所示，新型超声振动内圆磨削系统由振子、套筒、轴承、磨头套、非接触电信号传输系统、连接轴、联轴器、电动机、超声波发生器等构成。振子由一个半波长超声换能器和一个半波长变幅杆构成，砂轮粘接在变幅杆前端，振子通过两个节面位置法兰与套筒连接构成主轴部件，主轴部件通过前后轴承支撑在磨头套上，电动机通过联轴器和连接轴驱动主轴部件及砂轮进行旋转。振子在超声信号激励下产生一定频率的超声振动，砂轮也随之具有相同频率和一定幅值的超声振动，当砂轮与工件内表面接触时即可实现工件的超声振动内圆磨削加工［2］。

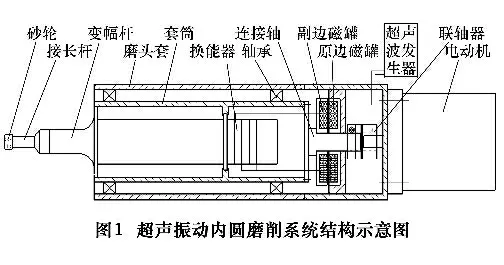
以往的旋转超声加工系统中的电能信号传输多采用碳刷、集流环连接的传输方式，这种方式存在碳刷、集流环滑动磨损较快、大量发热、裸露导线、转速不宜过高等缺陷。新型超声振动内圆磨削系统采用了旋转式非接触电信号传输系统，该旋转式非接触电信号传输系统中固定不转的原边磁罐线圈在接收超声波发生器发出的超声波电信号后会在其周围产生高频磁场，副边磁罐线圈在接收高频磁场能量后感应出与原边同频率的超声波电信号，副边磁罐线圈的输出端与换能器相连并驱动换能器工作，从而实现振子系统带动砂轮一起做超声振动。

1.1 振子的有限元分析

基于以往振子设计和修正过程中出现的问题，先以变截面杆波动方程推导计算换能器、变幅杆的几何尺寸［3-4］，然后直接对振子进行整体振动特性分析设计、制造、修正，使其前后法兰处纵向振动幅值均接近于零，而砂轮前端振幅达到内圆磨削加工所需要的范围。避免了换能器和变幅杆连接时的谐振修正问题，也降低了其连接处的能量损耗，且更易实现整体谐振。振子整体纵向振动模态及其沿轴线纵向振动相对振幅如图2 所示。

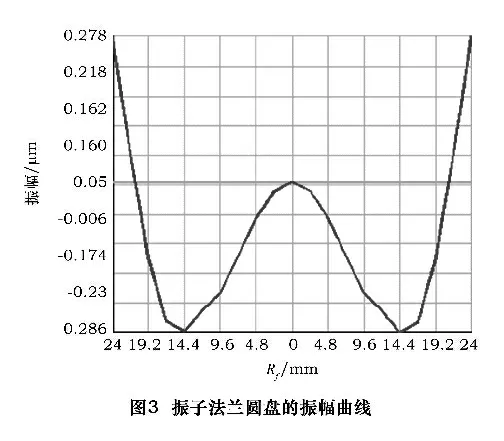
振子前端法兰圆盘的振动情况如图3 所示，说明振子法兰圆盘是在做弯曲振动。根据有限元分析法兰直径和厚度对法兰外圆处振动的影响规律，尽量使其外圆直径处的振动最小，优化后取法兰半径R1=24 mm，厚度L1=2 mm。

1.2 主轴结构的有限元分析

过去振子和套筒按振动理论分别设计，通过振子节面处的法兰和套筒相连。但实际上振子节面处法兰上存在的振动会影响主轴部件的振动特性。在新型超声内圆磨削系统设计中，把刚性连接的振子和套筒作为整体来进行分析设计，就不用考虑套筒对振子振动模态影响的问题，而且能够保证主轴的回转精度［5］。

在振子产生共振时，套筒的表面会产生一定强度的振动。为保证主轴工作正常，套筒上与轴承相配合的前后支撑轴径部分（图4 中的B、D 点）以及中间部分用于支撑振子后端法兰的位置（图4 中的C 点）应处于无振动状态。图5 是套筒长度为139 mm 时，套筒表面上各点的纵向振幅。从法兰的零位置开始，套筒外圆上沿轴线方向的纵向振幅呈振荡周期变化，靠近法兰位置的纵向振幅最大，而距法兰一定距离的位置及套筒另一端的位置，纵向振幅都接近于零。

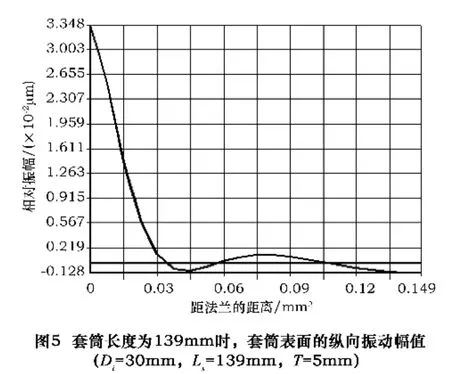
对图4 的结构，分析在不同套筒长度和厚度时，外圆表面上B、C、D 三点的振动变化规律，以振子输出幅值与A 点的振幅比为目标函数，以套筒内径、长度、厚度为变量，对套筒进行结构优化设计，找出在套筒上纵向振动幅值最小点。可以得到套筒的结构优化参数为Di=30 mm，Ls=145 mm，T=5 mm。应用上述参数的主轴结构有限元模态如图6 所示。主轴部件轴承的安装位置选在套筒表面振动最小位置（图4 中B、D 点），这样既能保证主轴部件的高精度运转，又可以减小轴承和磨头套对整个主轴部件振动特性的影响。

2 新型超声振动内圆磨削系统的实验研究

2.1 新型超声振动内圆磨削系统振子振动实验研究

在内圆磨削加工过程中，砂轮振幅是其主要工作性能指标之一。利用PSV -1 -400 型激光多普勒测振仪可以直接测试振子砂轮端面及法兰盘上实际的振动频率、振动幅值和振动状态。将制作的整体式振子平放，砂轮端面与激光入射方向垂直，如图7 所示在砂轮端面和法兰面上布置均匀的测振点，测得砂轮端面纵向振动频率为26.31 kHz、位移振幅为7.9 μm。法兰外径最大处的位移振幅均值为0.34μm，频率同为26.31 kHz。图8 为其振动状态。

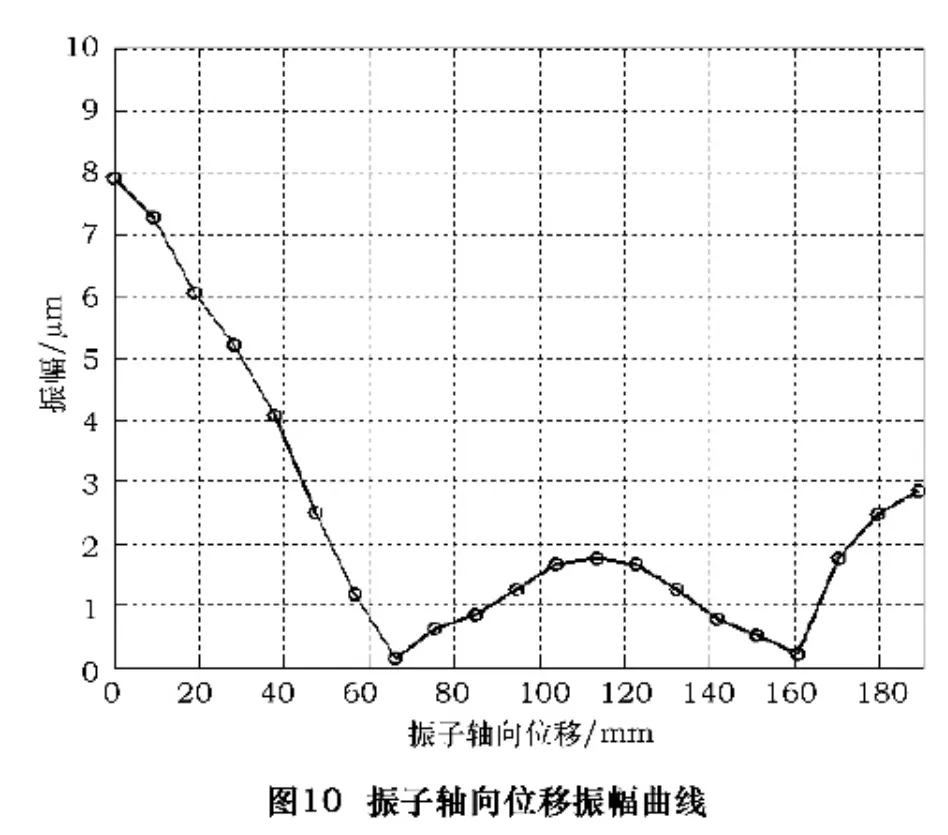
由于PSV -1 -400 激光多普勒测振仪不能直接测试振子的轴向振动位移曲线，根据三维测试原理对该测振仪进行改造后可以测出振子沿轴线表面的振动位移振幅曲线，在振子上布置测试点如图9 所示，其纵向振动测试曲线如图10 所示。

2.2 主轴振动特性实验研究

对振子加套筒后的主轴部件实际振动状态进行测试，判断法兰振动对套筒振动状态的影响。图11 所示为砂轮头端面和压紧端盖表面的振动测试点，其测振结果如图12 所示，砂轮头端面的纵向振动频率和位移振幅和未加套筒时相同。因此可得出结论：添加的套筒不影响振子的固有频率，砂轮头仍然保持其原有的输出功率，振子工作正常。压紧端盖表面的振动幅值远小于法兰盘的振动幅值，端盖上测点的振幅均值为0.08 μm，说明振子法兰并没有激起压紧端盖的振动，套筒和压紧端盖不影响振子系统的振动状态。

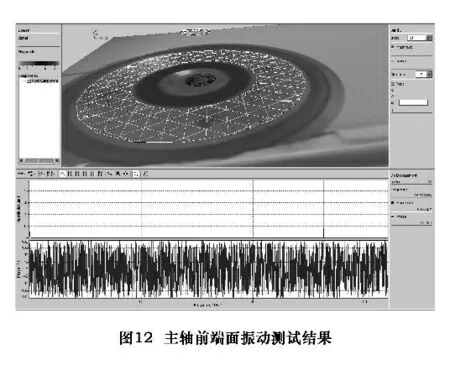
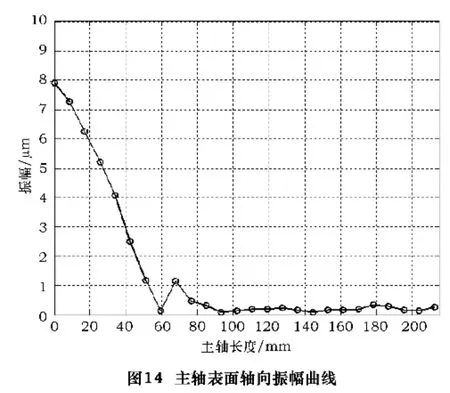
如图13 所示，采用同样的改造方法使用PSV -1-400 激光多普勒测振仪在主轴轴线上布置测试点，测试主轴表面沿轴线方向的振动位移幅值曲线。其纵向振动曲线如图14 所示，主轴前端振子振幅和振子单独测试时的振幅一致，套筒表面的轴向振动幅值都很小，均值为0.27 μm，并且在两个轴承和后辅助法兰安装处的振幅均达到最小值，轴承和后辅助法兰安装位置均在最优点，和有限元分析结果一致。

2.3 超声振动内圆磨削系统实验研究

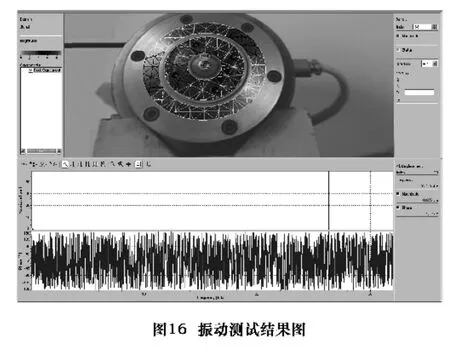
对机电匹配调试后的超声振动内圆磨头样机进行整体振动测试实验。磨头前端的砂轮端面、压紧端盖端面和磨头套端面上的测试点如图15 所示，测试结果如图16所示，砂轮端面振幅基本保持在7.9 μm 左右，且振动频率和振幅与振子单独测试时相同，因此可得出以下结论：套筒、轴承和磨头套等零部件不影响振子的振动状态，振子工作正常。而压紧端盖和磨头套端面的振动幅值较小，也说明振子传递到压紧端盖和磨头套的振动很小。

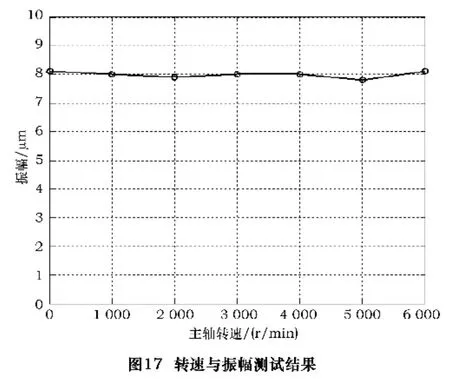
磨头转速在0～6000 r/min 之内变化时砂轮端部输出振幅变化曲线如图17 所示，砂轮端部的振幅基本保持在7.9 μm 左右。可以得出结论：砂轮端的振幅基本不受磨头转速影响。同时也验证了新型超声内圆磨削系统中的旋转式非接触电信号传输系统的良好性能，达到了对旋转式非接触电信号传输的设计目的。

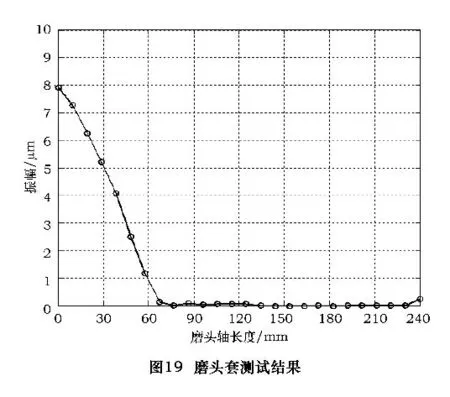
采用改造后的激光测振仪对超声内圆磨削系统的磨头套进行测振实验，如图18 所示测试点分布在磨头套轴线上，测出内圆磨削系统沿轴线表面的振动位移幅值曲线如图19 所示，可以看出磨头套表面的振动相对很小，均值为0.033 μm，并且成周期分布，轴承安装位置也在磨头套的纵向振动位移幅值最小位置，这有利于提高磨头主轴部件的回转精度。

3 结语

基于有限元方法，对超声振动内圆磨削系统中的振子、主轴部件分别进行了整体分析，并依据影响因素提出了新型超声内圆磨削系统的设计方法。通过对振子、主轴部件以及超声波振动内圆磨削系统整体的激光多普勒测振实验研究，验证了新型超声内圆磨削样机和理论设计方案的一致性和有限元分析方法的指导作用。设计制造的新型超声振动内圆磨削系统、旋转式非接触电信号传输系统工作正常，在额定转速下能够实现砂轮的有效纵向超声振动，试加工磨削性能良好。本文的创新点在于对超声内圆磨削系统采用了整体分析研究的思想和该磨削系统采用了一种新型的旋转式非接触超声电信号传输装置。

［1］隈部淳一郎.精密加工一振动切削基础和应用［M］.北京：机械工业出版社，1985.

［2］李华.超声波纵向振动内圆磨削系统的振子设计研究［J］.金刚石与磨料磨具工程，1998（5）：23 -25.

［3］陈桂生.超声换能器设计［M］.北京：海洋出版社，1984.

［4］林仲茂.超声变幅杆的原理和设计［M］.北京：科学出版社，1987.

［5］李华，李征.基于有限元的超声波内圆磨削的主轴设计与研究［J］.制造技术与机床，2008（3）：135 -139.