变倾角传递系数法及其在水电站滑坡分析中的应用

李建明

(中国水电顾问集团成都勘测设计研究院,四川 成都 610072)

1 前 言

在水电站工程建设中,边坡(或滑坡)的稳定性计算、分析以及处理是一项十分常见而且重要的工作,也是一个方兴未艾的工程地质及岩土力学课题。目前针对边坡稳定性定量计算的极限平衡法有多种,但是每种方法都有不足之处,有的原理易懂、计算简单,但是误差较大,适用范围小;有的推理严谨、误差较小、适用范围广,但十分深奥,计算工作极其浩繁,大多要借助大型的计算机软件,因而不够实用。在普通水电站工程中对边坡(或滑坡)的稳定性进行计算分析时,一般采用简单实用的算法,但为了减小误差,必须十分注意各算法的不足之处,对算法进行修正或重新演绎。为此,笔者根据条块在极限平衡状态下的静力平衡方程重新推导了传递系数法的另一种计算公式,暂称为变倾角传递系数法,它和传统的传递系数法相比,其表达式及计算过程均有区别。理论及实践表明,变倾角传递系数法比传统传递系数算法更通用,计算误差更小。

2 公式推导

如图 1所示,边坡潜在滑移体被分成 n个边界垂直的条块,右图为任一条块 i的受力状况。

图中:

Pi——i条块下部分界线受到的条间力(Pi-1同理);

βi—— Pi方向的水平倾角(βi-1同理 );

Wi——i条块的重量;

Ks——地震影响系数,KsWi为水平地震力;

Ni——i条块受到的底面法向支撑力;

Ri——i条块的条底抗剪力;

αi——i条块底滑面的水平倾角;

P0——滑动面进口的推力(极限平衡状态下为 0);

Pn——滑动面出口的推力,即 n条块的下部分界线推力(极限平衡状态下为 0)。

第 i条块垂直及水平方向的静力平衡方程为:

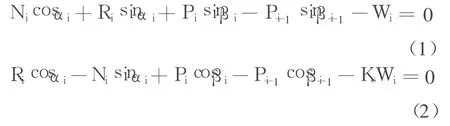
设整个滑动面的安全系数为 F,则在极限平衡状态下的条底抗剪力 Ri为:

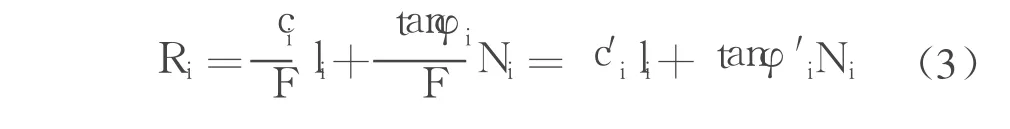
式中 ci、φi——潜在滑动面本身的抗剪强度参数内聚力和内摩擦角;

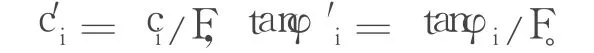
将式(3)代入式(1)、(2)并联立消去 Ni,可得极限平衡状态下的条块间作用力 Pi的递推公式(暂不考虑地震影响,即 Ks=0):

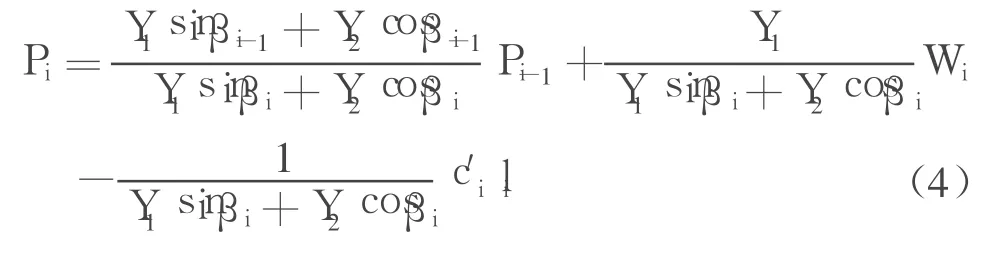
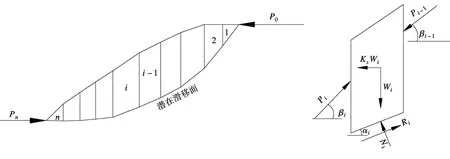
图1 条分及条块受力分析

在式(5)中令αi=βi,变形后就变成传统的传递系数法计算公式。这也说明传统的传递系数法认为条块下部分界线的条间作用力方向与条块底滑面平行,是造成传统方法计算误差相对较大、不适合倾角产生陡缓突变的滑动面的重要原因。而本文的算法把条间作用力方向的水平倾角 βi当作变量处理,可根据实际情况逐个调整条块分界线上的条间作用力倾角(尤其是传统方法不适合的陡倾角或陡缓倾角突变的滑面段),因而本文算法被称为变倾角传递系数法,和传统传递系数法相比具有一定的通用性。

3 计算方法

下面先给出土质边坡或松散体边坡不同滑面情况的条间作用力水平倾角 βi的简化表达式。可以证明,这样做是合理的,计算误差在允许范围内,算出的安全系数 F接近实际。

(1)如果条块 i的底滑面倾角 αi≤45°,且滑动面相邻两段的倾角没有较大突变情况。研究发现,条间作用力倾角 β与滑坡体的内摩擦角 φa、滑动面的内摩擦角 φ以及条块底滑面的倾角 α有密切关系,两者关系可简化为线性正相关。极限平衡状态下,对各内摩擦角进行强度折减后,其值变为 φ′a和 φ′,由于滑坡体在条块分界线上处于非常稳定的状态,远未达到破坏,因而条间力在条块分界线上的分力应该明显小于条块分界线上的最大抗剪力,又由于土体的内聚力c值一般很小,所以条间力水平倾角β一般应该小于或者略大于滑坡体内摩擦角φ′a,在 α不太大的情况下(即 α≤45°)介于 α与 φ′a之间,接近两者的均值,即对于 i条块而言,可设 βi=0.5×(αi+φ′a);如果土质边坡(或滑坡)为完全均质的,滑动面与滑坡体组成物质相同,则 φ′a=φ′i,于是 βi=0.5 ×(αi+φ′i)。参考其他算法对 βi的假定,这里的简化方式是合理的。

(2)如果条块 i的底滑面倾角 αi＞45°,或者与邻近的下部 i+1条块底滑面陡缓突变,则在式(5)的两边对 βi求导数,当 Pi取极值时导数 dPi/dβi=0,此时 βi=βi0=αi-φ′i,即为所需的条间作用力水平倾角 βi值。

按照上面的方法得到 βi的表达式后,就可利用式(5)进行安全系数计算了。过程如下:

先用最简单的瑞典条分法算出一个临时安全系数值 F0,将 F0、βi表达式代入式(5),滑动面入口的初始推力值(条块 1的 Pi-1值)P0=0,以此为初值,从条块 1依次算到最后的条块 n,可得每个条块下部分界线的 Pi值,最后一个条块 n的 Pi值Pn即为滑面出口的推力值。如果 Pn=0,或者非常接近 0(即其绝对值∣ Pn∣小于一个很小的正数,如 0.1),则所采用的安全系数值 F0为正确值,即可终止计算;如果 Pn＞0,且大于一个给定的正数(如 0.1),则适当减小 F0的值,重复上面的步骤再次计算,直到 Pn的值符合要求;如果 Pn＜0,且其绝对值∣ Pn∣大于一个给定的正数(如 0.1),则适当增加 F0的值,重复上面的步骤再次计算,直到Pn的值符合要求。Pn符合要求时对应的 F值,即为所求的安全系数值。

4 实际应用

算例 1:对文献[1]中例 4-4的某水电站均质黏土边坡,用本文的方法进行计算,再将计算结果和文献[1]的计算结果进行比较。土的容重γ=20kN/m3,内聚力 c=10kN/m2,内摩擦角 φ=26.6°。边坡计算剖面见图2。

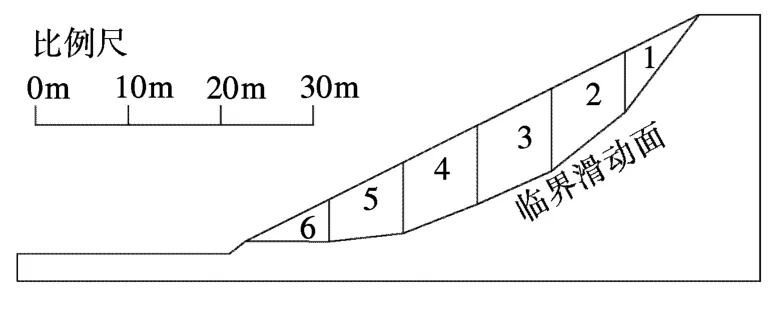
图2 算例 1计算剖面

用变倾角传递系数法算得图中临界滑动面的安全系数值 F=1.439,试算的典型数据见表1。文献里用权威的 Spencer法及 Morgenstern-Price法算得的结果为 1.437～1.442,简化 Bishop法的计算结果为 1.442,都和本文方法的计算结果 1.439吻合得非常好。文献里用传统传递系数法的计算结果为1.462,误差相对较大。

表1 安全系数 F的典型试算数据

算例2:文献[2]对某水电站的块石料场上部边坡进行了详细的计算、分析和研究,得出了科学合理的稳定分析成果及支护处理结论。其核心计算剖面如图 3(a)。潜在滑移范围为基岩上部的松散堆积物及变形体,组成物质共分 3层,从上到下依次为坡积物、变形体块碎石以及古滑坡滑带物质,在剖面上的分布范围如图 3(a)所示,可作为黏性土滑坡来处理。滑坡体各组成物质的物理力学参数见表2。计算中用到的关键潜在滑动面有两个:浅部的临界滑动面以及深部的基岩顶面,两个滑动面在下部重合,浅部滑动面为圆弧形,深部滑动面为折线形。文献[2]为了提高极限平衡法的计算准确度,将深部滑动面简化为与折线尽可能多重合的圆弧。从图3可知,上部的折线陡缓突变处与简化圆弧没有重合。在本例的计算中,为了验证变倾角传递系数法是否适合陡缓突变的折线滑动面,特意将原来使用的滑动面稍作修改,使滑动面在上部与折线完全重合。计算条分见图3(b)。

根据上述条件,用变倾角传递系数法算得两个潜在滑动面的安全系数分别为:临界滑动面 F1=1.13,深层滑动面 F2=1.10。文献[2]用简化毕肖普法算得临界滑动面 F1=1.08,用有限元法算得临界滑动面 F1=1.25,深部滑动面 F2=1.19。最后,笔者用权威的 M-P法算得深部滑动面 F2=1.074,用传统传递系数法算得 F2=1.212。毕肖普法和 M-P法是计算安全系数的权威算法。可见,变倾角传递系数算法得到的安全系数误差明显小于传统传递系数法,说明算法是可行的、实用的。顺便指出,由于以上计算过程深部滑动面采用的是上部陡缓突变的折线滑动面,不适合用传统的传递系数法来计算,而用本文的变倾角传递系数法计算的结果比较合理,这说明了变倾角传递系数算法在计算陡缓突变的折线滑动面时,和传统传递系数法相比,大大减小了安全系数的计算误差,在一定程度上克服了传统传递系数法的某些不足。

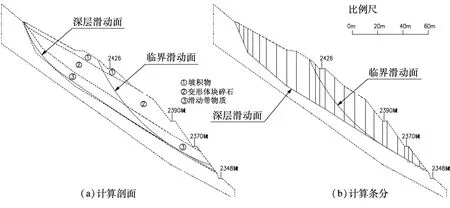
图3 算例 2计算剖面图及条分示意

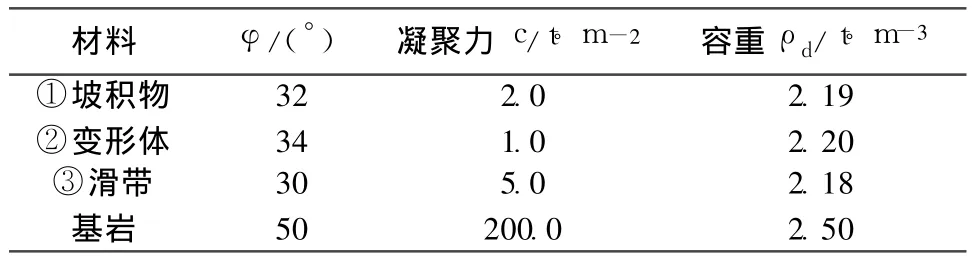
表2 边坡稳定计算参数(天然工况下)

5 结 语

本文重新推导的计算边坡稳定性的变倾角传递系数法和传统的传递系数法相比,计算公式更加简洁整齐,便于理解、计算和记忆,适用范围比传统的传递系数法大,计算陡倾角或陡缓突变的折线滑动面的误差远小于传统传递系数法,克服了传统算法的某些不足。由于把条间作用力的方向倾角当作变量来处理,可以根据实际情况灵活地给每一条块分界线设置不同的、合理的条间作用力倾角,使得计算结果比传统传递系数法更加接近实际,克服了传统算法“因不能改变条间作用力方向而引起较大误差”的问题。此外,本文给出的各种情况下条间作用力倾角的简化公式肯定有不足之处和局限性,但由于本文的变倾角传递系数法将条间作用力方向作为变量来处理,具有一定的通用性,在以后的进一步研究中,一定可以找出更加准确、更加合理的条间作用力倾角表达式,然后代入本文的公式进行计算,就可以得出更准确的计算结果。

[1]陈瑞泽,王天一.边坡与滑坡工程治理新技术应用手册[M].北京:地质出版社,2009.

[2]杨建,江平,何绍明.西尔料场边坡稳定性分析专题报告[R].成都:中国水电顾问集团成都勘测设计研究院,2009.

[3]马永潮.滑坡整治及防治工程养护[M].北京:中国铁道出版社,1996.

[4]张卓元,王士天,王兰生.工程地质分析原理[M].北京:地质出版社,1993.

[5]陈希哲.土力学地基基础[M].北京:清华大学出版社,2004.