钢梁整体稳定性实验结果分析

2010-04-19乐风江

四川建筑 2010年1期

王亮,乐风江

(新疆大学建筑工程学院,新疆乌鲁木齐 830008)

梁是结构的主要构件,梁的整体失稳可能导致整个结构丧失承载能力,甚至造成严重的工程事故。在高等院校中为学生开设钢梁整体稳定性实验,可以提高学生对稳定性理论的感性认识,加深理论知识的理解。然而,往往实验的数据所得结果与规范公式相差较大。如何对实验结果进行分析,找到影响实验结果的各种因素,使实验的精度得到进一步提高,尚需要做深入的工作,从而加深对钢结构稳定性理论的认识和理解。

1 工字型截面钢梁丧失整体稳定性实验概况

为了提高学生对钢结构稳定性的理论认识水平,我校近些年为学生开设了钢梁整体稳定性实验,实验采用工字型截面组合钢梁。加载设备采用 Q30B-02-00高精度液压油缸伺服系统,用DH 3818静态电阻应变仪进行上下翼缘的应变测量,百分表测量侧向及竖向位移。

下面仅抽取 1组(3根)典型的实验进行分析研究,3根尺寸完全相同编号分别为 1号、2号、3号,材料为 Q235-B钢,支座采用自制夹支支座,利用分配梁加载。1#至 4#和 5#至 8#测点读数分别表示上下翼缘应变值 ε。1#至 6#和 7#百分表分别测量钢梁侧向及竖向位移,实验模型及加载方式如图 1及图 2。

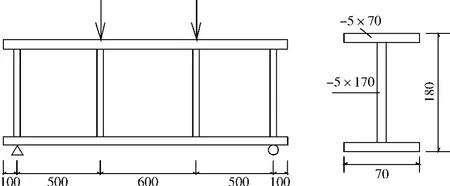
图1 钢梁具体尺寸

钢梁开始加载后,首先出现竖向位移同时伴随有侧向变形,但竖向变形数值较小,上下翼缘应变逐渐增大。在荷载达到一定程度的时候,竖向位移较为明显,侧向位移也逐渐缓慢增大,当荷载达到某一数值,钢梁出现较为突然的侧向扭曲(侧向变形变得很大)不能继续承载,从而丧失整体稳定,如图 3所示。

实验时每加 1级荷载,稳定 5min左右再读数。记录应变值 ε及挠度值,并绘制出 P-ε、P-f曲线。

图2 试验梁加载

图3 试验梁破坏

1号钢梁得到 P-ε、P-曲线如图 4,图 5所示。

图4 1号钢梁荷载 -应变曲线

图5 1号钢梁荷载 -挠度曲线

2号钢梁得到 P-ε、P-f曲线如图 6、图 7所示。

图6 2号钢梁荷载 -应变曲线

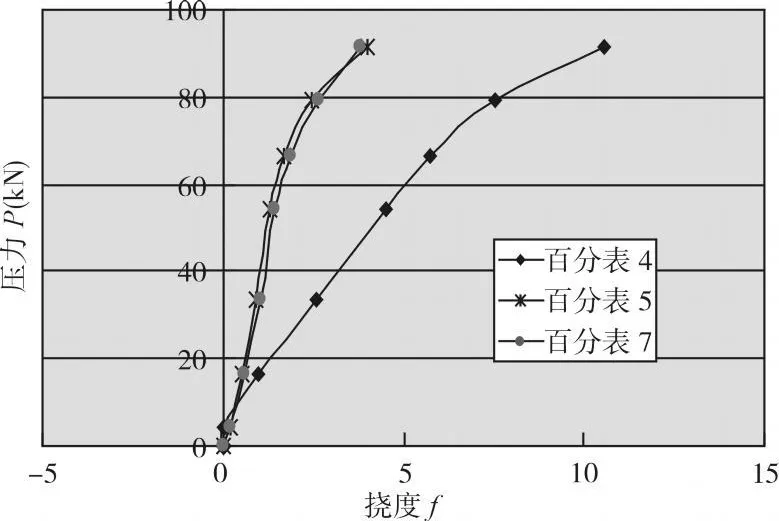
图7 2号钢梁荷载 -挠度曲线

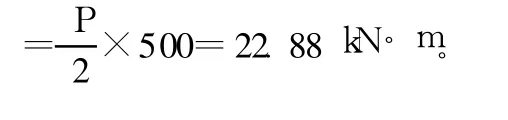
3号钢梁得到 P-ε、P-f曲线如图 8、图 9所示。

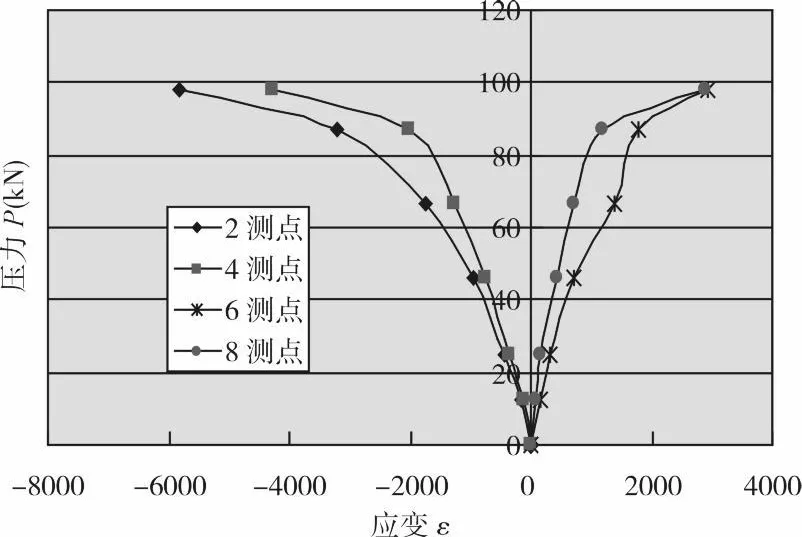
图8 3号钢梁荷载 -应变曲线

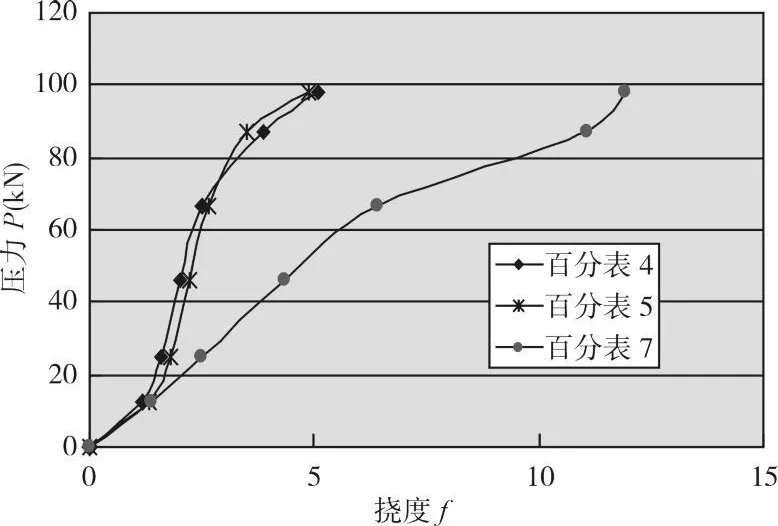
图9 3号钢梁荷载 -挠度曲线

由于发生突然的侧向扭曲,最后一级读数没有来得及读出,但其结果应与 1、2钢梁相近,取 3号钢梁的极限荷载为97.76 kN,Mcr=(P/2)×500=24.44 kN·m。

取 3根钢梁所得临界弯矩平均值为实验测得临界弯矩,即 Mcr=24.27 kN·m。

2 钢梁整体稳定性实验结果分析

通过规范公式、静力法和能量法对临界弯矩 Mcr公式进行计算。

2.1 钢梁的临界弯矩理论值

(1)由规范中对钢梁整体稳定部分说明得,钢梁整体稳定性验算公式为:

(2)由三轴平衡方程关系(静力法),列出平衡微分方程:

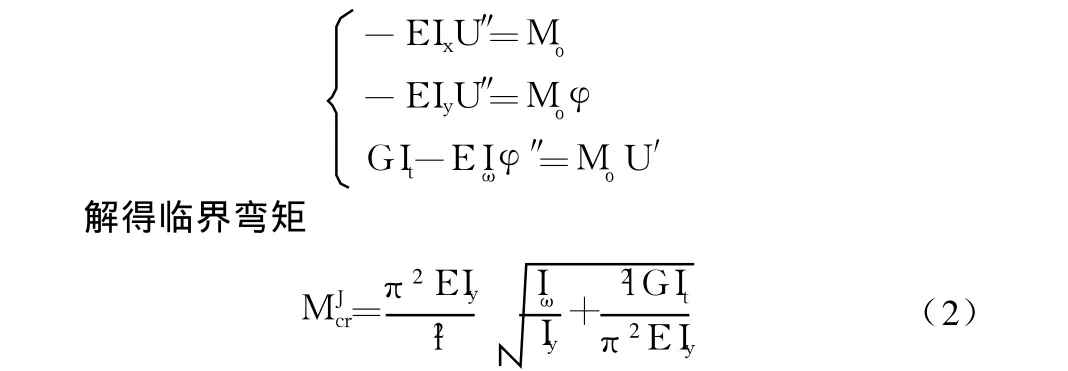
(3)实验采用两点加载能量法,力分别为 P/2,列出总势能方程为:

把所得数据结果代入静力法和能量法所得临界弯矩式式(1)、式(2)、式(3)中得:

2.2 实验数值与理论值对比分析

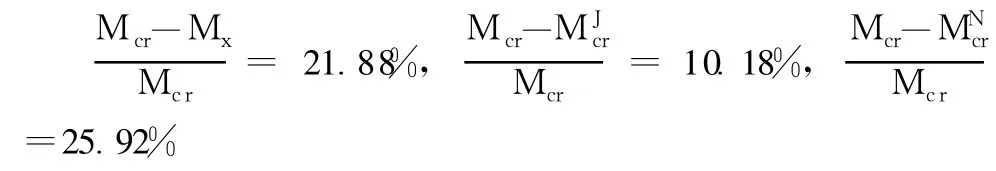
实验所得结果与规范公式、静力法、能量法所计算的数据分别相差 21.88%,10.18%,25.92%。

根据 3组实验与理论值结果对比发现,理论公式和规范公式解得的临界弯矩的结果都与实验所得结果有一定的偏差。究其原因,有以下几点因素影响:(1)由于实际设计出的钢梁要为人们所应用,应当更安全一些,实际钢梁要比理论公式计算的结果偏大;(2)学生做实验时,完成测量、记录等工作时,产生一定误差,钢梁放置时有一定初偏心和钢梁有残余应力的作用;(3)实验仪器输出结果有一定误差。