MPT方法中的纳米粒子识别技术
2010-04-15王绪伟李战华
王绪伟 ,李战华
(中国科学院力学研究所非线性力学国家重点实验室,北京100190)
0 引 言
MPT(Multiple-Particle Tracking)也叫多粒子追踪,是测量粒子布朗运动的一种方法,其原理是连续记录多个粒子的运动图像,通过图像处理获取粒子布朗运动位移。粒子布朗运动曾被用于测量Avogadro常数、Boltzmann常数等[1-2],近来用于测量细胞内的结构和流变特性等[3-4],因此MPT方法在胶体科学和生物细胞研究等领域有重要的应用前景。
MPT方法包括图像采集和图像处理两个部分。图像采集是利用CCD连续记录粒子运动图像。图像处理可细分为:图像滤波、粒子识别、粒子匹配和扩散系数计算4个步骤[5-6]。图像滤波是为了消除粒子图像中的背景灰度不均匀和单点噪声。粒子识别是为了提取光斑位置。粒子匹配是对相邻两帧图像上的粒子进行配对,判断粒子同一性,以便计算其位移。
目前MPT图像处理中大多使用Crocker[5]给出的图像处理算法。粒子识别环节是图像处理的关键,通常采用的单一灰度阈值在识别粒子凝聚团、粒子的衍射光晕等时会出现错误。为了剔除“伪粒子”,Crocker[5]曾提出了利用粒子光斑一阶矩和二阶矩的散点图,将图中零零散散的光斑予以剔除。Sbalzarini[7]对错点剔除办法进行了改进,提出了选择剔除粒子量化公式。改进后可以有效剔除粒径过大或形状不规则的粒子,如聚集状态的粒子团。Patrik[8]根据离焦平面越远粒子衍射图像越大的原理,提出了剔除非焦平面粒子的办法,即以粒子光斑的直径为阈值,滤除偏离焦平面的光斑过大的粒子,并用0.925μ m粒子验证了此方法有效性。但这一技术仅剔除非焦平面的粒子,并未包括光斑是否代表真实粒子的判断。由于纳米粒子粒径小、光强弱,实验中通常要使用高倍数的物镜和高灵敏度的EMCCD。高倍数的物镜焦平面较薄,粒子容易形成光晕;而高灵敏度的EMCCD有利于采集微弱的光强信号,但当粒子光斑和光晕的灰度差别不大时,二值化处理中粒子图像中的衍射光晕容易离散化形“伪粒子”,因此需要探索新的粒子识别方法。此外,MPT程序中,粒子匹配结果的正确性一直是大家关心却不能妥善解决的问题。一种办法是使用数值算法生成模拟粒子运动轨迹和图像序列,然后用实验程序追踪模拟粒子图像,并与已知的粒子运动轨迹进行比较[4]。但是对模拟粒子图像的追踪效果并不能完全代表对真实图像的处理,而且该方法并不能直观地标记追踪中发生错误的位置和错误的原因,不利于针对错误原因改进算法。
因此,通过测量直径200nm的荧光粒子在纯水中的布朗运动,在开发粒子追踪程序中研究纳米粒子光斑识别和匹配效果的可视化技术。通过调整灰度阈值比较粒子光斑面积变化进行“伪粒子”剔除。为了比较手动与程序追踪的粒子匹配效果,提出矢量判别法显示粒子匹配效果。通过测量φ 200nm粒子扩散系数验证粒子追踪法的有效性。
1 实验与图像处理方法
实验在中物院力学所 LNM室进行。采用O-lympus IX71倒置荧光显微镜,配有NA=1.35的100倍油镜进行观测。图像采集使用Andor iXon885 EMCCD,在bing 2模式下为501×502像素,像素尺寸为160nm/像素。实验用粒子为200nm直径的聚苯乙烯荧光粒子(Duke Scientific),荧光的吸收和发射波长分别为532nm和615nm。实验时,荧光粒子在超纯水中稀释至体积分数约为10-5。
实验溶液配置后的5~10min内开始实验。将约50μ L含纳米荧光粒子的溶液滴到盖玻片上,如图1,液滴的直径约3mm。CCD焦平面调至距离玻片上表面约10μ m。图像采集时连续两帧的时间间隔Δ t为36.5ms,其中包括图像曝光时间约10ms和图像传输时间。在同一位置连续拍摄200帧图像。用4个液滴重复上述实验,每次实验持续时间为20~25min。实验温度在20~23℃±0.1℃,单次实验过程中温度变化小于±0.3℃。

图1 实验装置示意图Fig.1 Schematic of the experimental setup
用手动追踪和MPT程序追踪分别进行图像处理。手动追踪是指人工进行粒子定位和匹配。对连续两帧图像进行粒子配对后得到多个粒子的单步位移Δx,然后对连续200帧图像进行同样的处理,获得多个粒子的连续位移。根据Einstein公式,单个粒子运动的二维均方位移为

其中Δx为间隔时间Δt内粒子的单步位移。对多个粒子的均方位移采用系综平均计算,得到实验扩散系数Dexp为
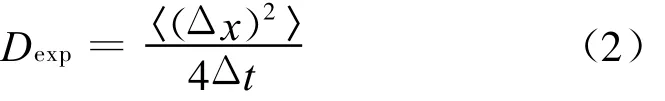
2 实验结果
2.1 粒子识别的错点剔除技术
对点光源进行成像时,由于散射和镜头球差的存在,成像光斑为一个圆斑和一个同心圆环的光晕。偏离焦平面中央的荧光纳米粒子光斑外有明显的光晕。MPT方法处理时,首先设定灰度阈值将图像转换为二值化图像。部分带光晕的光斑经过二值化转换后,光晕被离散成多个片段,如图2(a)。在粒子识别时,这些光晕片段被当作粒子光斑,形成“伪粒子”。由于纳米粒子成像时,本身光斑直径较小,亮度较低,使用现有的基于光斑形态和灰度大小的算法很难有效剔除这类“伪粒子”。
我们发现,假设在图像二值化时所使用的灰度阈值改变量为 Δ G,粒子光斑和光晕的面积都有变化,但粒子光晕片段在低灰度阈值下相互连通,导致其面积变化Δ Sc比粒子光斑的面积变化Δ Sp更明显。图2(b)显示,当 ΔG变化3%后,ΔSp≈20像素,而 ΔSc≈200像素。利用这一现象,在二值化过程中调整灰度阈值并检测光斑面积变化,就可以有效地剔除“伪粒子”。

图2 图像二值化中不同灰度阈值时粒子光斑与光晕的面积变化Fig.2 The area varieties of one particle spot and its diffraction rings under different grayscale thresholds
2.2 粒子匹配的矢量判别法
对实验拍摄的图像分别采用手动追踪和程序追踪。将相邻两帧图像中粒子匹配的结果以箭头形式绘制,其中箭头的起点为粒子起始位置,箭头的大小和方向代表该粒子在Δ t时间内的单步位移,如图3。布朗运动是随机的,因此矢量的方向任意,但矢量的大小可由已知粒子直径代入Einstein-Stokes公式进行估计,因此矢量大小直观地显示了可能发生错误匹配的位置。假设手动追踪的矢量场可靠,程序追踪与手动追踪矢量图的夹角也提示用软件进行粒子匹配可能发生错误,从而为改进MPT算法提供依据。根据公式(1),φ 200nm粒子的平均位移大小为4~5像素,而通常引起伪粒子识别的光晕距离粒子光斑中心为5像素以上,因此MPT程序的伪粒子识别将引起矢量夹角大于60°。当调整程序追踪中使用的灰度阈值到2%后,所得到的矢量与手动追踪的矢量图基本相同,有一对错误,如图3(a),图中较小的矢量夹角是由于手动和程序追踪使用了不同亚像素算法引起的。此外,粒子识别时的灰度阈值高低影响被追踪的粒子个数。高阈值(如5%),图3(b)未发现程序匹配错误,但部分粒子没有被程序识别。此结果也说明矢量法还可以直观判断图像识别时选择的阈值的效果。正是分析图3(a)中的错误匹配的粒子光斑,才发现了由于光晕引起的“伪粒子”问题。
2.3 错点剔除算法验证
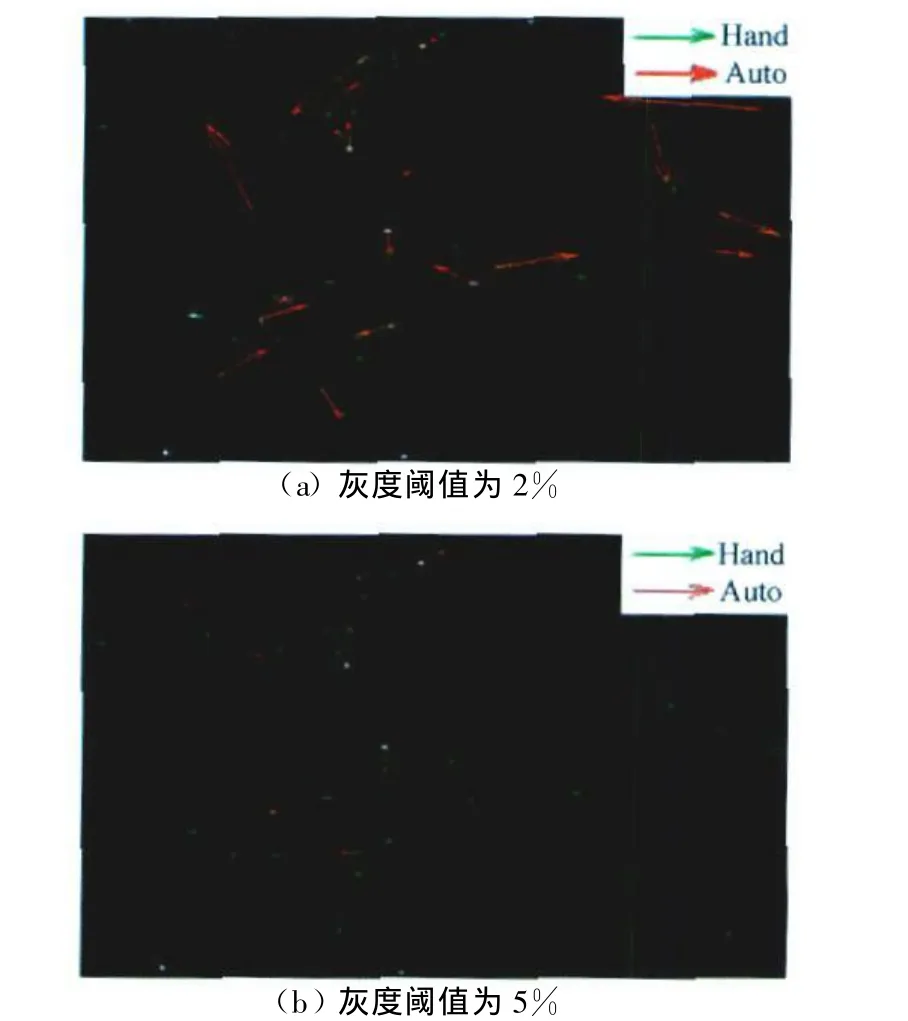
图3 粒子匹配手动追踪(绿色)和程序追踪(红色)的粒子矢量位移比较Fig.3 Displacement vercors of the track results by MPT program(red)and by hand(green)
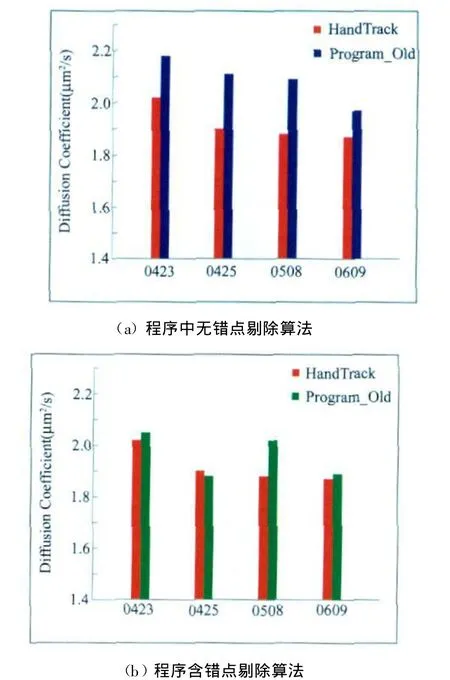
图4 手动追踪和程序追踪给出的φ 200nm粒子实验扩散系数测量结果的比较(横坐标为实验日期)Fig.4 The experimental diffusion coefficients of 200nm particles measured with MPT and by hand
为了验证2.1节提出的光斑错点剔除法和2.2节的粒子匹配矢量法,我们对φ 200nm粒子进行扩散系数测量实验。图像处理分别使用手动追踪和程序追踪,然后利用公式(2)计算实验扩散系数。对4次实验,程序中不含有错点剔除算法时,追踪结果与手动追踪相比偏差很大约为8%~13%,如图4(a);程序包含错点剔除算法后的实验扩散系数基本与手动追踪的结果相同,如图4(b),4次试验中的3次中二者偏差不到2%,另外一次的偏差也降低为8%。
由于实验拍摄的粒子图像并不完全相同,因此每批实验图像应该先选取一些使用手动追踪。然后用MPT程序处理与手动结果比较,对灰度阈值进行选择使二者结果一致,再用程序代替手动追踪。
3 结 论
采用MPT方法测量200nm直径的粒子在纯水中的扩散系数,在手动追踪粒子位移的同时自主开发了程序,发现现有MPT方法缺乏对粒子匹配效果的直观显示,影响对匹配算法的改进,而且纳米粒子光晕会影响粒子识别,因此提出下述改进技术:
(1)在粒子识别过程中,调节灰度阈值并检测粒子光斑面积变化,基于光斑及光晕的面积对阈值的敏感性可以有效地剔除光晕类“伪粒子”;
(2)在粒子匹配过程中,将连续两帧中粒子位移用矢量表示,可以直观显示MPT方法中粒子匹配效果。
φ 200nm粒子扩散系数测量的实验表明,在MPT方法中增加上述粒子识别法手动追踪和程序追踪获得的实验扩散系数的偏差由8%~13%减小为2%~8%,这表明使用基于光斑面积阈值敏感性的算法来剔除光晕引起的“伪粒子”是合理、有效的。
[1]PERRIN J B.Atoms,2nd English edition[M].London:Constable,1923.
[2]NAKROSHIS P,AMOROSO M,LEGERE J,et al.Measuring Boltzmann's constant using video microscopy of Brownian motion[J].Am.J.Phys.,2003,71(6):568-573.
[3]LIU J,GARDEL M L,KROY K,et al.Microrheology probes length scale dependent rheology[J].Physical Review Letter,2006,96:118104.
[4]SERGE A,BERTA UX N,RIGNEA ULT H,et al.Dynamic multiple-target tracing to probe spatiotemporal cartography of cell membranes[J].Nature Methods,2008,5(8):687-694.
[5]CROCKER J C,GRIER D G.Methods of digital video microscopy for colloidal studies[J].Journal of Colloid and Interface Science,1996,179(1):298-310.
[6]王绪伟,李战华.SPT方法在纳米粒子布朗运动观测中的应用[J].实验流体力学,2008,22(1):84-87.
[7]SBALZARINI I F,KOUMOUTSAKOS P.Feature point tracking and trajectory analysis for video imaging in cell biology[J].Journal of Structural Biology,2005,151:182-195.
[8]SAVIN T,SPICER P T,DOYLE P S.A rotional approach to noise discrimination in video microscopy particle tracking[J].Applied Physics Letters,2008,93:024102.
[9]EINSTEIN A.Investigations on the theory of the Brownian movement[M].Dover Publishing,INC.,1956.
