利用博弈思想对暗标投标的分析

2010-04-14张志刚

山西建筑 2010年16期

张志刚

在招投标过程中，业主与投标人之间，投标人与投标人之间，投标人与监督机构之间存在信息不对称的情况，因此招投标过程是众多利益方的博弈过程。

1 博弈论

博弈论是20世纪40年代形成并发展起来的研究冲突对抗条件下最优决策问题的理论。博弈论认为:1)人是理性的，即人都会在约束条件下最大化自身的利益;2)人们在交往合作中有冲突，行为互相影响，而且信息不对称。

1886年，法国经济学家莱昂◦瓦尔拉斯在其著作《纯粹经济学要义》中，第一次用数学方程式的形式表达了一般均衡的概念。具体说来，瓦尔拉斯隐含地假定存在一个投标人，他负责喊出所有商品的价格，所有的市场主体都在瞬间得到这些价格信息(即完全信息假定)，并很快根据对商品的需求函数和供给函数计算出他们对商品的需求和供给数量，假定这一切均无成本。如果在这一价格下，不能使所有商品市场出清，则没有任何交易发生;或者供求双方可以试签合同，但如果发现市场尚未出清，则重新签订合同，直到投标人喊出均衡价格，这时交易都在此均衡价格下进行，所有商品市场全部出清。

2 招投标的博弈分析

2.1 招投标博弈特征分析

招投标是一种特殊的交易活动，在这种交易活动中，招标人与投标人各自的利益目标是不同的。招标人希望以最低的合理标底获得最优的中标单位;而投标人则希望以最有竞争力的报价和最低的成本中标。招投标双方在利益目标上既有一致性又有对立性，都希望交易成本最小化，价值最大化。

所谓不完全信息，是指每个投标商在开标前均知道自己对标的物的价值估量和自己的生产成本，而不知道其他投标商对标的物的价值估量和生产成本，但是他对其他投标人可能的价值估量和生产成本有一个主观判断概率。

所谓非合作博弈是指在博弈过程中，投标人之间无法达成具有约束力的协议，他们的决策是独立做出的。招投标博弈是一种静态博弈，因为招投标过程具有一次性特征，所有投标人的投标行为可以被认为是同时做出的，没有先后之分。

2.2 招投标的博弈分析

假设以 AH和AL表示高报价和低报价，以DG和DB表示好的投标人和差的投标人的工程成本，以DOG和DOB表示好的投标人和差的投标人的未中标的损失，以 VG和VB表示好投标人和差投标人中标时业主的收益，若无投标人中标，则业主的收益为0。再假设:不管投标人是好的还是差的，承包工程后都努力工作，因而给业主创造的收益都大于投标价格。但差的承包人给业主创造的收益要小，即 VG＞VB＞AH＞AL;工程要达到预定的质量、工期、费用等方面的要求，差的承包人的努力成本要比好的承包人高，即DB＞DG;好的投标人未中标的损失要比差的投标人大，即DOG＞DOB;好的投标人和差的投标人类型各占1/2，即 p(G)=p(B)=1/2;好的承包人报低价的概率较大而差的承包人报高价的概率较大，即 p(H/G)≤p(L/G)，p(L/B)≤p(H/B)。

给定以上假设，博弈行为的顺序如下:首先“自然 N”选择投标人的类型是好还是差。然后，投标人根据自己的类型选择高报价还是低报价。最后，业主根据投标人的报价来判断投标人的类型从而选择中标人。业主面临三个选择，即选择高报价投标人中标还是低报价投标人中标或者不选择投标人中标。

业主选择中标的收益期望值要大于不中标的收益期望值;业主选择低价中标的收益期望值要大于高价中标的收益期望值。因此，业主会采用低价中标的方式才能使自身利益最大化。

若有 n个投标人，给定投标人 i的成本d和其投标报价a，则其支付的期望值为 ui=(a-d)p(a＜ai)，这里 p(a＜ai)是 a＜ai的概率，ai是投标人i的报价，a-d是中标者的净收益。可求得该博弈的贝叶斯均衡解为a*(d)=d(n-1)/n。

可以看出，当n→∞时，a*→d。投标人越多，各个标价就越接近实际成本。因此，业主应该采用公开招标的形式，使更多的投标人参与投标，这样就能以更低的价格获得承建商，实现业主利益最大化。而对投标人而言，报价越低，中标的可能性就越大。

3 博弈论思想对暗标投标的分析

基本的暗标投标规则是各投标人密封标书投标，统一时间开标，标价最高者中标。如果出现标价相同的情况，用抛硬币或类似方法决定中标者。假设有两个投标人，分别为1，2，投标人 i对商品的估价为vi，即如果投标人i付出价格p得到商品，则i的收益为vi-p。两个投标人的估价相互独立，并服从[0，1]区间上的均匀分布。投标价格不能为负，且双方同时给出各自的投标价。出价较高的一方得到商品，并支付他报的价格;另一方的收益和支付都为0。投标方风险是中性的，所有以上都是共同信息。

为把这一问题化为标准式的静态贝叶斯博弈，我们必须确定行动空间、类型空间、推断及收益函数。参与者 i的行动是给出一个非负的投标价bi，其类型即他的估价 vi(在抽象博弈中表示为 G={A1，A2;T1，T2;p1，p2;u1，u2}，行动空间 Ai=[0，∞)，类型空间 Ti=[0，1])。由于估价是相互独立的，参与者 i推断服从[0，1]区间上的均匀分布，而不依赖于 vi的值。最后，参与者 i的收益函数为:

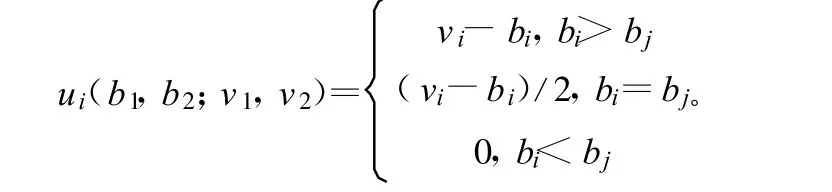
为推导这一博弈的贝叶斯纳什均衡，我们首先建立参与者的战略空间。在静态贝叶斯博弈中，一个战略是由类型到行动的函数。参与者 i的一个战略为函数bi(vi)，据此可以决定i在每一种类型(即对商品的估价)下选择的投标价格。在贝叶斯纳什均衡下，参与者1的战略b1(v1)与参与者 2的战略 b2(v2)互相是对方的最优反应。若战略组合[b1(v1)，b2(v2)]是贝叶斯纳什均衡，那么每个类型 vi∈[0，1] ，bi(vi)满足:

由于参与者的估价是均匀分布的，这样的线性均衡解不仅存在，而且是唯一的。其结果为 bi(vi)=vi/2，也就是说，每一参与者以其对商品估价的1/2作为投标价。这样，一个投标价格反映出投标方在投标中遇到的最基本的得失权衡:投标价格越高，中标的可能性越大;投标价格越低，一旦中标所得的收益就越大。

假设参与者 j采取战略bj(vj)=aj+cjvj，对一个给定 vi的值，参与者i的最优反应为下式的解:

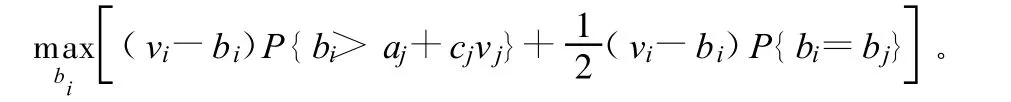
因为vj服从均匀分布，所以 bj(vj)=aj+cjvj服从均匀分布，P{bi=bj}=0。由于 i的投标价应高于参与者j最低的可能投标价格，否则没有意义，同时应低于j最高的可能投标价格，我们有 aj≤bi≤aj+cj，于是，上式变为:

一阶条件为bi=(vi+aj)/2。在 vi＜aj时，bi=(vi+aj)/2＜aj，这样是根本不可能中标的，至少 bi=aj。综上，参与者 i的最优反应为:

如果0＜aj＜1，则一定存在某些 vi的值，使 vi＜aj，这时bi(vi)就不可能是线性的了，而在开始时是一条直线，后半段开始向上倾斜，与假定的线性矛盾。而只讨论 aj≥1及 aj≤0的情况。但前一种情况是不可能在均衡中出现的，因为估价较高一方对投标价的最优选择是不低于估价较低一方的投标价，我们有 cj≥0，但这时aj≥1便意味着bj(vj)≥vj，而这对于参与人 j肯定不是最优的。因此，如果要求bi(vi)是线性的，则一定有 aj≤0，这时 bi(vi)=(vi+aj)/2=ai+civi，于是可得 ai=aj/2及 ci=1/2。

同样对参与者j重复上面的分析，得到类似的结果aj=ai/2及ci=1/2。解这两组结果构成的方程组，可得 ai=aj=0及ci=1/2，即 bi(vi)=vi/2。