遗传算法在教学任务分配中的应用

刘青凤

LIU Qing-feng

（安阳工学院，安阳 455000）

遗传算法在教学任务分配中的应用

Apply the genetic algorithm in teaching task distributing

刘青凤

LIU Qing-feng

（安阳工学院，安阳 455000）

本文通过对教学任务表中三要素的分析，利用遗传算法实现了教学任务表的分配工作，从而使人们从繁杂的手工操作中解脱出来，提高了工作效率。

遗传算法；教学任务表；基因；染色体；种群；遗传算子

0 引言

在学校的日常教学管理工作中，教学任务表的设计是最重要也是最基本的环节，而课表则是实施教学计划的具体表现方式。教学任务的分配和课表的制作是进行教学管理的开始，它们在执行教学计划这一教学管理中心环节中起着极其重要的作用，通过它们对教学活动和教学秩序实施科学的组织和管理，因此，课程编排问题在一定程度和深度上影响着学生学习培养与教学质量的提高。

目前，由计算机进行排课的软件已经很多，而教学任务表的设计还停留在手工阶段。对于那些只拥有几百名学生，数十名教师的小规模学校来说，手工进行计划表的设计还能应付，但随着我国教育体制改革的深入，学生人数不断增加，专业设置、课程设置不断向深度和广度发展，教师队伍也在不断壮大，如果还要拿出教师名单、班级课程去进行逐个手工填写，工作量大、效率低下的缺点就显露无遗。本文将使用遗传算法来解决教学任务表的合理分配。

1 遗传算法的基本过程

遗传算法是John.H.Holland根据生物进化的模型提出的一种优化算法，它是基于进化过程中的信息遗传机制和优胜劣汰的自然选择原则的搜索算法。它是从代表问题可能潜在解集的一个种群开始的，而一个种群由经过基因编码的一定数目的个体组成。每个个体实际上是染色体带有特征的实体。染色体作为遗传物质的主要载体，即多个基因的集合，其内部表现是某种基因组合决定的。初始种群产生以后，按照适者生存和优胜劣汰的原理，逐代演化产生出越来越好的近似解。在每一代，根据问题域中个体的适应度大小挑选个体，并借助代表自然遗传学的遗传算子进行组合交叉和变异，产生出代表新的解集的种群。这个过程导致种群象自然进化一样，后代种群比前代更加适应于环境，末代种群中最优个体经过解码，可以作为问题的近似最优解。

2 教学任务分配表三要素

排课涉及的相关问题主要包括：时间、班级、课程、教室和教师5个要素，而教学任务分配表所涉及到的有班级、课程和教师3个要素，对这些问题的透彻分析和适当的处理是开始算法设计的基础。

2.1 时间

在排课问题中涉及关于时间的概念有学年、学期、周、天、课时。根据大专院校的教学特点，工作日为周一至周五共5天，一天安排6节课，上课方式为一次两节课，即每天分三个时间段。关于时间片的设计在课程表编排时很重要，在教学任务计划表的编排过程中未涉及，这里不再赘述。

2.2 课程与教师

在教学计划中，课程是学生上课的具体内容。课程有自己的编号、课程名、课程类型等，每门课程都有指定的教师，这样可以把课程和教师作为同一变量来考虑。

2.3 班级和教室

一般情况下，学校安排各班级的理论课程均在各自的固定教室，在这种情况下，把班级和教室当作一个变量等同考虑，

2.4 教师

每个教师都拥有自己的编号、姓名、可任课程、最大课时数等。在分配教学任务时，在不超过最大工作量的前提下，尽量平均分配每位教师的周课时数。

教学任务分配实际上是计算领域中一个有约束的组合优化问题，它将班级、课程与任课教师组成一维，使排课最终形成班级、教室和时间的三维，其关系如图2所示。

由图示可以看出，教学任务分配表的设计就是将班级、课程和教师三个要素合成一维的过程，它是课程表编排的前提和基础，它的变动将影响到排课的全局。

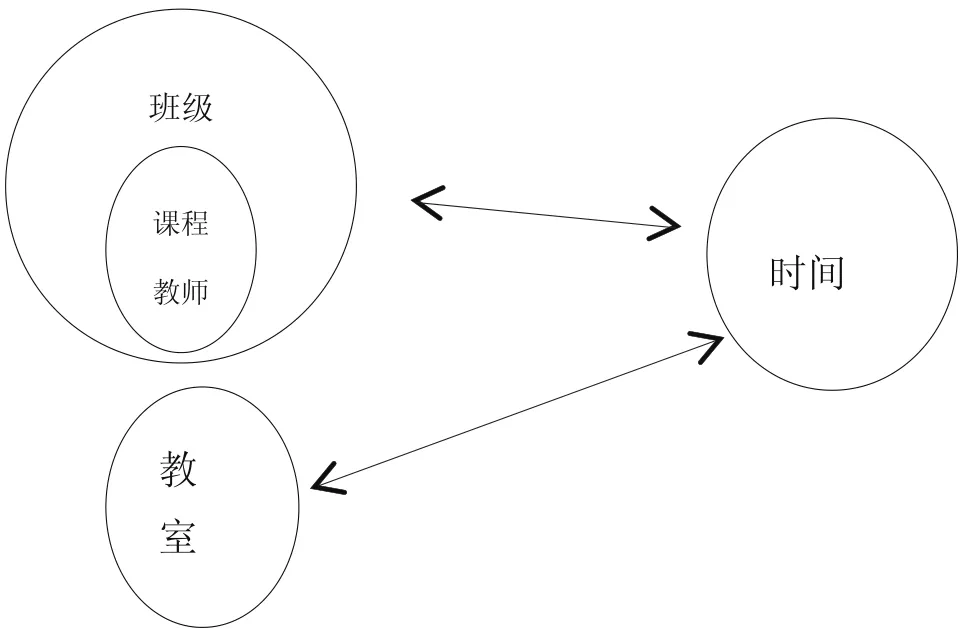
图1 基本元素关系

3 教学任务分配表遗传算法设计

3.1 总体设计

本阶段实现班级、课程和教师的三维合一。

3.1.1 数据表设计

本过程所用表集合及其属性如下：

教学任务表teachtask.dbf(任务编号，课程号，课程名，班级号，教师号，周次数，教室类型)，教学任务分配即要填写本表中每一个任务要分配给的教师号，正是本文要完成的工作。

教师表teacher.dbf（教师号，姓名，性别，职称，出生日期，可任课程号，已排课时数，最大课时数，期望值），本表是计算适应度函数的重要依据。

课程表course.dbf（课程号，课程名，周次数）

班级表class.dbf（班级号，教室号，学生人数，专业，）

教室表classroom.dbf（教室号，座位数）

评价表eva.dbf(f,v,p ,q) 本表是对所选m个样本进行评价。其中f的值为样本表名称teachtask&i(i=1,2……m)；v为评估值（越小越好），p为样本的选择概率，用maxv表示v的最大值，sumv表示maxv-v之和，则p=(maxv-v)/sumv；q为累计概率。

选择样本表taskselection.dbf(任务名，q，r)本表存放进行轮盘赌程序操作时，所选中的表。其中，任务名为teachtask&i(I=1，2……m)，q同评价表eva.dbf中的属性，r为轮盘赌程序中的随机参数，该值与q值比较，确定是否选择对应的任务表。

图2 初始种群中的两个个体

3.2 遗传算法设计步骤

3.2.1 初始化种群

复制教学任务表teachtask.dbf到teachtask&i.dbf，作为一个“个体”，每张表中的一行，称为一个“染色体”，在表的教师号字段列随机填写可任该课程的教师号，所填写的教师号称为“基因”。从第一个个体的第一个染色体开始填充基因，直到种群规模为M的M个个体全部填写完成为止，这样就形成了M个初始的教学任务表。本过程即选择M=20张教学任务表teachtask1……teachtask20，每张表中，将各教学任务安排教师来担任，即为每个班的各门课程安排一位教师。并限定教师的最大课时数和该教师可任课程，安排课程应在此范围内。在此限定条件下，为每项任务随机安排教师。此运行结果，相应产生M=20个教师教学统计表teacher1……teacher20，其中统计出每位教师的总课时数和所任课头数。

3.2.2 构造适应度函数(countks.prg)

评估函数有两个指标，第一，为每位教师安排课程的总课时数t应当平均，差别不要太大；第二，尽量安排少的课头数。计算教师课时数的平均值av，用各自总课时数t与平均数av的差。对每个个体teachtask&i，计算s(i)=∑(abs(t(j)-av))(j=1，2……k k为教师人数；i=1，2……m。 m为个体数)。教师课头数对应的期望值如表1所示。

表1 教师课头数期望值

计算总期望值b(i)= ∑a(j) (j=1,2……k i=1,2……m)

每个个体的评估函数值为：v(i)=sqrt(s(i)+b(i))值越小，价值越高。

3.2.3 设计遗传算子

1） 选择操作（wheelselection.prg）

本过程采用轮盘赌的方法选择父本。

轮盘赌选择模拟博彩游戏中的轮盘赌。一个轮盘被划分为n个扇形，每个扇形表示群体中的一个个体，而每个扇形的面积与它所表示的个体的适应值成正比，如图4所示。为了选择种群中的个体，想像有一个指针指向轮盘，转动轮盘，当轮盘停止后，指针所指的个体被选择。因此一个个体的适应值越大，表示该染色体的扇形面积越大，它被选择的可能性也就越大。实现步骤如下：

由于评估函数v（i）的值越小，价值越高，而轮盘赌是概率越大越容易被选中，所以

（1）用最大适应值maxv减去每个样本的适应值作为每个样本的适应值maxv（i）-v（i）；

（2）计算种群中所有个体适应值之和。sumv=∑(maxv（i）-v（i）)，i=1,2,3,……m；

（3）计算每个样本的选择概率。p=（maxv-v）/sumv；

（4）计算每个染色体的累计概率。q（i）=∑p（i），i=1，2，3，……m；

（5）转动轮盘m次，从中选出m个染色体。

实现过程如下：

随机产生一个0～1之间的数r来模拟转动一次轮盘后，轮盘停止转动后指针所指向的位置。若r≤q1，这说明指针指向第1个扇形，这时选择第一个个体teachtask1，一般若q（k-1）＜r≤q（k），这说明指针指向第k个扇形，这时选择第k个个体。

图3 表示6个染色体的轮盘

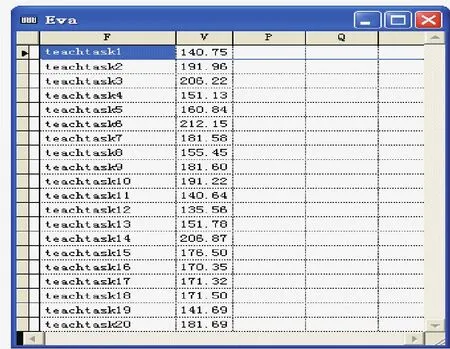
图4 教学任务适应度值表

2）杂交运算(cross1.prg)

采用传统的遗传算法单点杂交的方法，以Pm=0.25的概率选出个体，如果选取的是奇数个，则删除最后一个。对偶数个个体按顺序进行两两杂交。杂交的方法是：随机产生一个n（每个染色体teachtask&i中有n项任务）之间的整数K，两个染色体，均取K～n条记录，并将对应记录的教师号进行对换（如果教师不同，且课程在该教师可任课程中包括，则进行交换，否则不进行操作）。

3）变异操作(mutation1.prg)

经过杂交后的种群中的每一个个体（teachtask&i的每一个染色体（表中的一条记录），产生一个随机数random()，若random()<=pm，(pm为变异率，设为0.01)，那么该基因位进行变异，否则不变异。本过程的变异是更换任课教师：首先记录该染色体的课程号，在teacher.dbf中查找可任该课程的教师，并找到不同于当前染色体的教师号，更换之。

4）重新计算适应值进行评估(countks.prg/fit.prg)，选择最优个体。

4 结束语

一般的文章中，都将教学任务分配阶段的工作手工操作，排课系统直接从课表的编排入手，本文将排课表前期的教学任务分配使用遗传算法进行操作，这样设计的作用有：

1）提高了工作效率。每位教师所任课程存入数据库中，一般是固定不变的，不需每次都重新输入，可个别修改。然后，由计算机根据数据库中的数据分配任务，可以大大提高工作效率。

2）公平公正。很多教师不愿担任较差的班级，或不愿担任较难上的课程，手工分配任务时，要考虑这些不该照顾的对象，给教学任务分配工作造成不便。利用遗传算法，由计算机随机进行分配任务，可以杜绝此类事情的发生。

采用遗传算法解决教务方面的问题还是一个较新的研究领域，本文只是针对教学任务分配方面作一尝试，具有一定的局限性，对于比较复杂的问题还有待于进一步研究。

[1] Radcliffe N.J.The Alegbra Of Genetic Algorithms.Annals Of Math,&Al,1994,10:339-384.

[2] 陈根社,陈新海.遗传算法的研究与进展[J].信息与控制,1994,23(4):P215-222.

[3] 周明,孙树栋.遗传算法原理及应用[M].国防工业出版社,2002.5.1.

[4] Goldberg D E.Genetic Algorithm in Search, Optimization,and machine Learning.Addison-Wesley,Reading,MA,1989.

[5] Vittorio Maniezzo,Genetic Evolution of the Topology and Weight Distribution of the Neural Networks,IEEE,Trans.on Neural Networks,Vol.5,NO.1,1994,PP39-53.

[6] Zbigniew Michalewicz, David B. Fogel.曹宏庆,李艳,董红斌,吴志健译.如何求解问题一现代启发式方法[M].北京:中国水利水电出版社,2003.

[7] 尹朝庆.人工智能与专家系统[M].北京:中国水利水电出版社,2002,l.

TH166

A

1009-0134(2010)10(上)-0203-03

10.3969/j.issn.1009-0134.2010.10(上).63

2010-01-27

刘青凤（1970 -），女，安阳人，讲师，硕士，研究方向为计算机软件与理论。