非负矩阵最大特征值的新界值

李 华 (河南城建学院数理系,河南平顶山467044)

1 基本概念与引理

用A≥0(aij≥0)来表示A是非负矩阵,记ρ(A)为n阶非负矩阵A的最大特征值。

由G.Frobenius不等式[1]知:

对列和也有相同的结论。

对于有非零行和的非负矩阵,文献[2]把式(1)进一步作了改进,有:

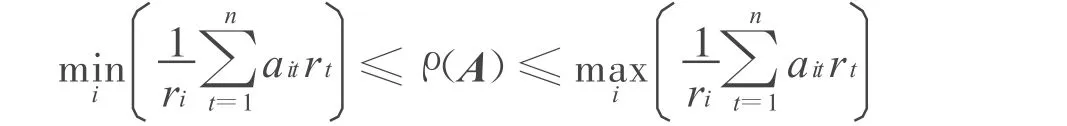
引理1[3]设A=(aij)为n阶非负不可约矩阵,B=(A+I)n-1,其中,I为n阶单位阵,则对任何正整数k有:

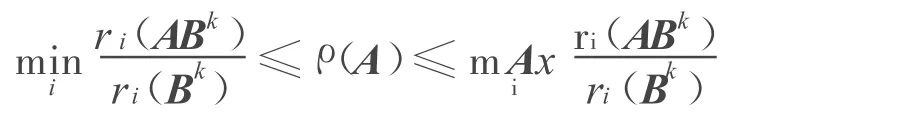
引理2[4]设A=(aij)为n阶非负不可约矩阵,若存在正整数k使得ri(Ak)≠0(i=1,2,…,n),则:

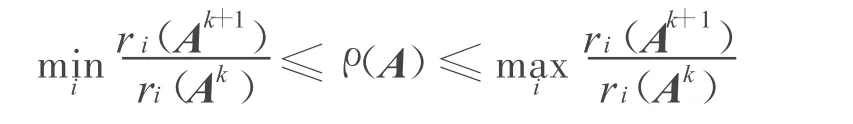
引理3[5]设A是n阶非负矩阵,若A有若干零行(列),设其编号为k1,k2,…,ks,化去A的k1,k2,…,ks行(列)以及k1,k2,…,ks列(行)后所得的矩阵为A1,则ρ(A1)=ρ(A)。

在以下的讨论中均设非负矩阵既无零行也无零列。下面,笔者在文献[2,3]的基础上给出非负矩阵最大特征值的新界值。

引理4[2]设α是矩阵A的特征值,X=(x1,x2,…,xn)T,Y=(y1,y2,…,yn)T分别是矩阵AT和A对应于α的特征向量,则:

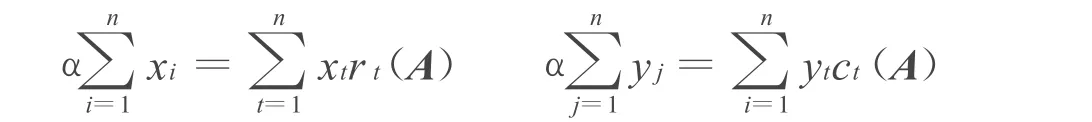
引理5[2]若q1,q2,…,qn是正数,则对任意实数p1,p2,…,pn,有:

引理6[6]设A是n阶矩阵,ri(Ak),ci(Ak)分别表示矩阵Ak的第i行行和与第i列列和,则:

2 主要结果

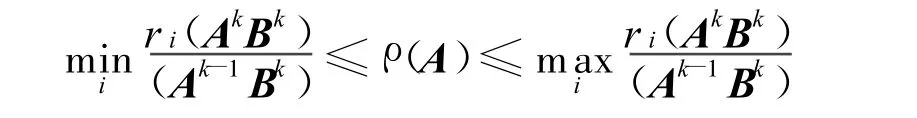
证明由于ri(B)≠0,则ri(Bk)≠0。设 X=(x1,x2,…,xn)T＞0,Y=(y1,y2,…,yn)T＞0分别是矩阵A和AT对应于ρ(A)的特征向量,且,则:

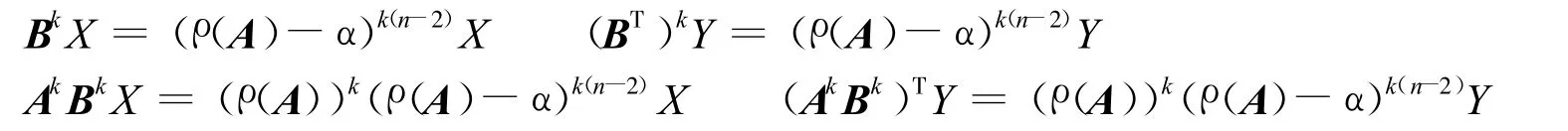
由引理4知:

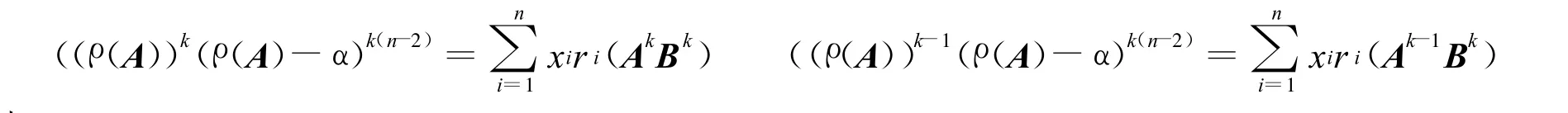
则:

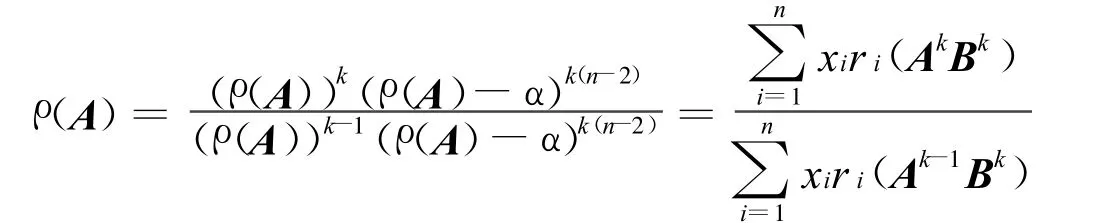
由引理5知:

定理2设矩阵则对任意正整数k,极限k和存在,且:

证明因为B=(A-αI)n-2,则有AB=BA,AkBk=ABAk-1Bk-1,则对任意正整数k,由引理5及引理6知:

即:

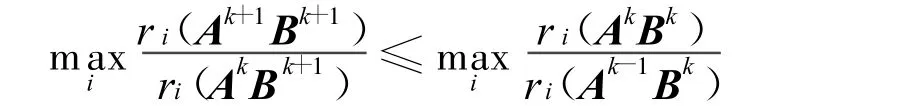
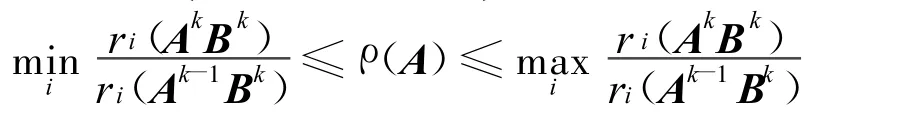
两边取极限,即:

对列和,也有类似定理1和定理2的结果。

3 数值算例

例1[4]设矩阵估计A的最大特征值。

A的最大特征值估计结果比较如表1。例1的实际结果ρ(A)=7.7290。由表1可以看出,定理1得到的结果在一定程度上要其他方法的结果更精确。

表1 最大特征值估计结果

[1]Frobenius G.Uber matrizen aus nich t negativen elementen[M].Berlin:S B P ress,1912.456～477.

[2]M inc H.Nonnegative Matrices[M].New york:Wiley,1988.11～19,24～36.

[3]殷剑宏.非负矩阵最大特征值的新界值[J].数值计算与计算机应用,2002,23(4):282～295.

[4]景何妨,尤伟华,司书江.非负矩阵最大特征值的新界值 [J].兰州大学学报 (自然科学版),2004,40(5):1～3.

[5]谈雪媛.有关非负矩阵半径及分离度的估计 [J].南京师范大学学报,2004,(1):24～27.

[6]Liu S L.Bounds for the greatest characteristic root of a nonnegativem atrix[J].Lin A lg Appl,1996,239:151～160.