32 m铁路简支梁模板优化设计

王利民

（中交第三公路工程局有限公司，北京 100102）

32 m铁路简支梁模板优化设计

王利民

（中交第三公路工程局有限公司，北京 100102）

介绍32 m铁路简支梁模板系统的优化设计方法，根据梁体预制时的实际荷载，对模板各部件进行了详细受力计算，并与通用模板进行了力学性能分析。

铁路简支梁；模板；优化设计

1 概述

专桥（01）2051-Ⅳ32 m梁，全长 32.6 m，梁高 2.5 m，顶板宽度为1.92 m。模板由板面系统、支撑系统和操作平台3部分组成。其中，板面系统包括面板、小肋、横肋和竖肋；支撑系统包括支撑架、侧顶杆、竖顶杆和横拉杆。一套模板分为内侧模板、外侧模板，每侧模板由4块模板组成（端部模板8.3m+中部模板8.0m+中部模板8.0 m+端部模板8.3 m）。

通用的制梁模板虽能满足制梁的各项要求，但十分笨重，不便于操作，加工制作费用较高。为了方便施工，降低劳动强度，减少模板加工制作费用，对通用模板进行了优化设计，根据模板在梁体混凝土施工时所受荷载，对模板各系统进行了受力计算，并对整个模板系统进行了有限元分析，设计出既符合制梁要求又方便操作的模板系统。

2 计算荷载

根据《铁路混凝土与砌体工程施工及验收规范》TB10210—2001之《附录A模板荷载》的规定计算。

2.1 新浇筑混凝土对模板的侧压力

实际施工时，梁体混凝土浇筑时间为3.5 h，梁高2.5 m，则混凝土浇筑速度为：V=2.5/3.5=0.72 m/h。混凝土振捣采用附着式振动器为主，插入式振动器为辅的施工工艺，则新浇筑混凝土侧压力为

Pmax=61×v/（v+0.4）=（61×0.72）/（0.72+0.4）=39.2 kPa

在进行模板验算时，取Pmax=40.0 kPa。

2.2 倾倒混凝土时因振动产生的水平荷载

施工时采用0.9 m3料斗，故按照规范要求得到作用于侧模上水平荷载为6 kPa。

2.3 混凝土侧压力分布图

新浇筑混凝土密度（碎石取2 500 kg/m3），则有效压力为：h=Pmax/25=40/25=1.6 m

按规范规定，需附加“倾倒混凝土时因振动产生的水平荷载”，附加范围为有效压力部分：6/25=0.24 m

侧压力分布图，见图1。

3 优化设计计算

3.1 双向面板计算

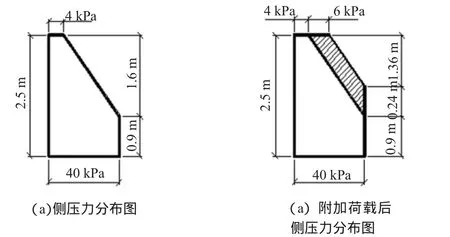
图1 侧压力分布图

面板取6 mm厚Q235钢板（原面板厚10 mm），根据混凝土浇筑情况见图2（a），取面板中的一个区格作为计算单元。图中A区格看做三面固结、一面简支；B区格看做四面固结；C区格看做两面固结、两面简支。取上述3种情况中最不利者进行计算。从受力观点看，A区格最不利。在模板面板中，区格取最大为500×563 mm进行计算见图2（b）。

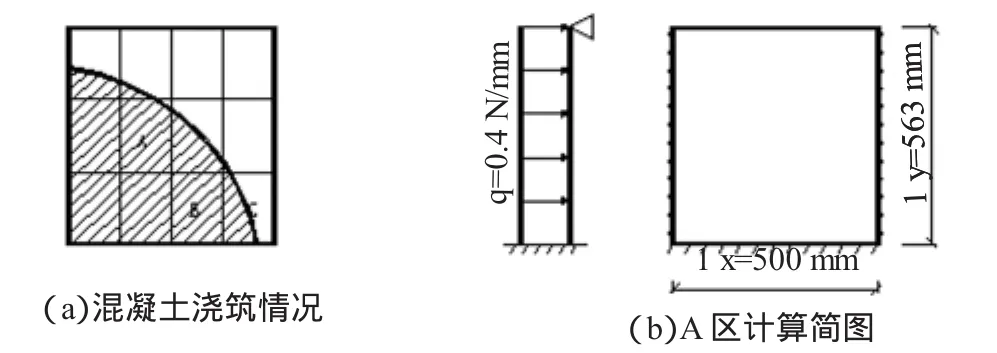
图2 面板计算简图

3.1.1 强度验算

取10 mm宽的板条作为计算单元。

计算荷载为：q=0.04×10=0.4 N/mm

M x0=Kqlx2=-0.066 9×0.4×5002=6 690 N·mm

M y0=Kqlx2=-0.056 4×0.4×5002=5 640 N·mm

截面抵抗矩Wx=Wy=bh2/6=10×62/6=60mm3

∴σx=M x0/W x=6 690/60=111.5N/mm2〈〔σ〕

σy=M y0/W y=5 640/60=94.0N/mm2〈〔σ〕

3.1.2 挠度验算

fmax=0.001 86ql4/K

而K=Eh3b/12（1-μ2）=2.06×105×63×10/12×（1-0.32）=40.747×106

∴fmax=0.001 86×0.4×5 004/40.747×106=1.14 mm〈〔f〕

3.2 小肋计算

横肋最大间距为563 mm，小肋最长者为563 mm，满焊在横肋上，故按两端固定梁计算，见图3。

3.2.1 强度验算

先确定板肋共同工作时确定面板的有效宽度b1。面板和小肋组合截面见图3。

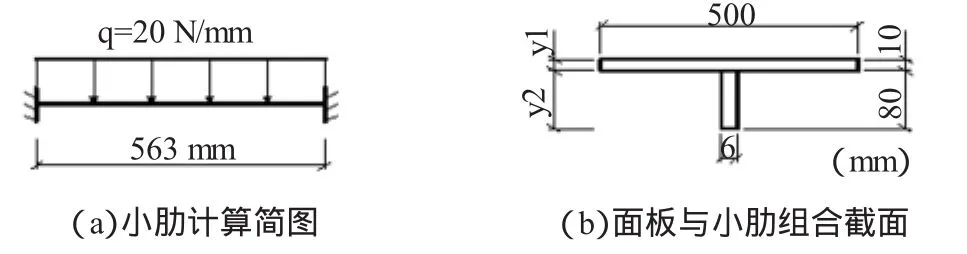
图3 小肋计算简图

截面积 A=500×6+80×6=3 480 mm2

面积矩 S=500×6×3+6×80×（40+6）=31 080 mm3

形心 y1=S/A=31 080/3 480=8.9 mm Y2=86-8.9=77.1 mm

截面惯性矩 I=500×63/12+500×6×（8.9-3）2+6×803/12+80×6×（77.1-40）2=103.01×104mm4

截面弹性抵抗矩

W上=I/y1=103.01×104/8.9=115.74×103mm3

W下=I/y2=103.01×104/77.1=13.36×103mm3

弯矩按两端固定梁计算：

M=-ql2/12=-20×5632/12=-528 282 N·mm

组合截面最大应力：

σ=M/W下=528 282/13.36×103=39.5 N/mm2

根据 σ=39.5N/mm2、b/h=500/6=83.33，查《手册》得 b1/h=70，即

b1=70×h=70×6=420 mm。

按计算b1强度验算

小肋的内力按三跨连续梁计算

M=KMql2=-0.117×20×5632=-741 707 N·mm

最大应力：σ=M/W下=741 707/13.26×103=55.9 N/mm2〈〔σ〕

3.2.2 挠度验算

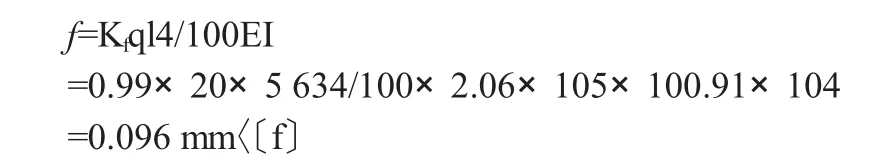
3.3 横肋计算

横肋与小肋、面板共同工作承受外力，计算方法同小肋。

竖肋最大间距为1 000 mm，横肋最长者为1 000 mm，满焊在竖肋上，故按两端固定梁计算，计算简图见图4。

计算荷载为：q=0.04×563=22.52 N/mm

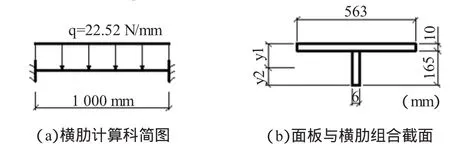
图4 横肋计算简图

3.3.1 强度验算

计算得板肋共同工作时确定面板的有效宽度b1=449 mm。最大应力σ=52.4 N/mm2〈〔σ〕

3.3.2 挠度验算

f=Kfql4/100EI=0.967×22.52×10004/100×2.06×105×754.65×104=0.14 mm〈〔f〕

3.4 竖肋计算

竖肋分两种：2[20和2[14b，以较小截面2[14b进行计算。竖肋间距为1 000 mm，中间有一根与竖肋同方向的小肋，故面板、小肋与竖肋共同工作。根据模板支撑架对竖肋的支撑情况，且竖肋与支撑架焊接成整体，构成共同承担水平和垂直方向荷载的骨架。故为简化计算，只计算腹板处竖肋，且近似地把竖肋内力按三跨连续梁计算，计算简图见图5。

计算荷载为：q=0.04×1 000=40 N/mm

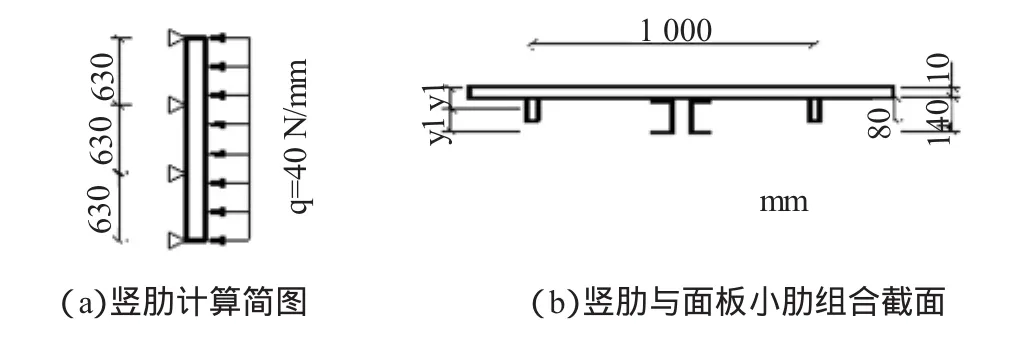
图5 竖肋计算简图

截面积 A=42.62×102+450×6=6 962 mm2

面积矩 S=42.62×102×（70+6）+450×6×3=332 012 mm3

形心 y1=S/A=332 012/6 962=47.7 mm Y2=（140+6）-47.7=98.3 mm

截面惯性矩

I=2 100.4×104 mm4

截面弹性抵抗矩

W上=I/y1=2 100.4×104/47.7=440.3×103mm3

W下=I/y2=2 100.4×104/98.3=213.7×103mm3

最大内力：弯矩按三跨连续梁计算，查《手册》得最大弯矩系数KM=-0.117

M=KMql2=-0.117×40×6302=-1 857 492 N·mm

最大应力：

σ=M/W下=1 857 492/213.7×103=8.7 N/mm2〈〔σ〕

挠度验算：

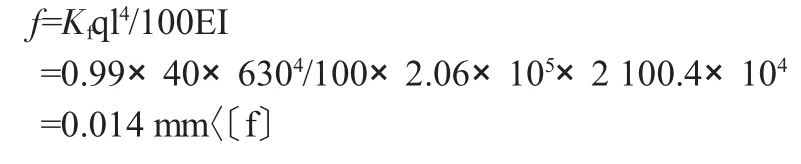
4 优化设计效果

从优化前后模板系统各部件的力学性能对比结果可以看出，优化设计前后的模板系统在满足相关规范和梁体施工要求的前提下，充分发挥了材料的性能，减轻了整体重量，方便了施工，降低了制作成本。优化前后对比见表1。

32m Railroad Simple Beam Template Optimization Design

Wang Limin

Introduces the 32m railroad simple beam template system’s optimization design method.Prefabricates when according to the Liang body the actual load，has carried on the detailed stress computation to template various parts，and has carried on the mechanical properties analysis with the general template.

railroad simple beam；template；optimization design

U445.471

A

1000-8136(2010)35-0062-03

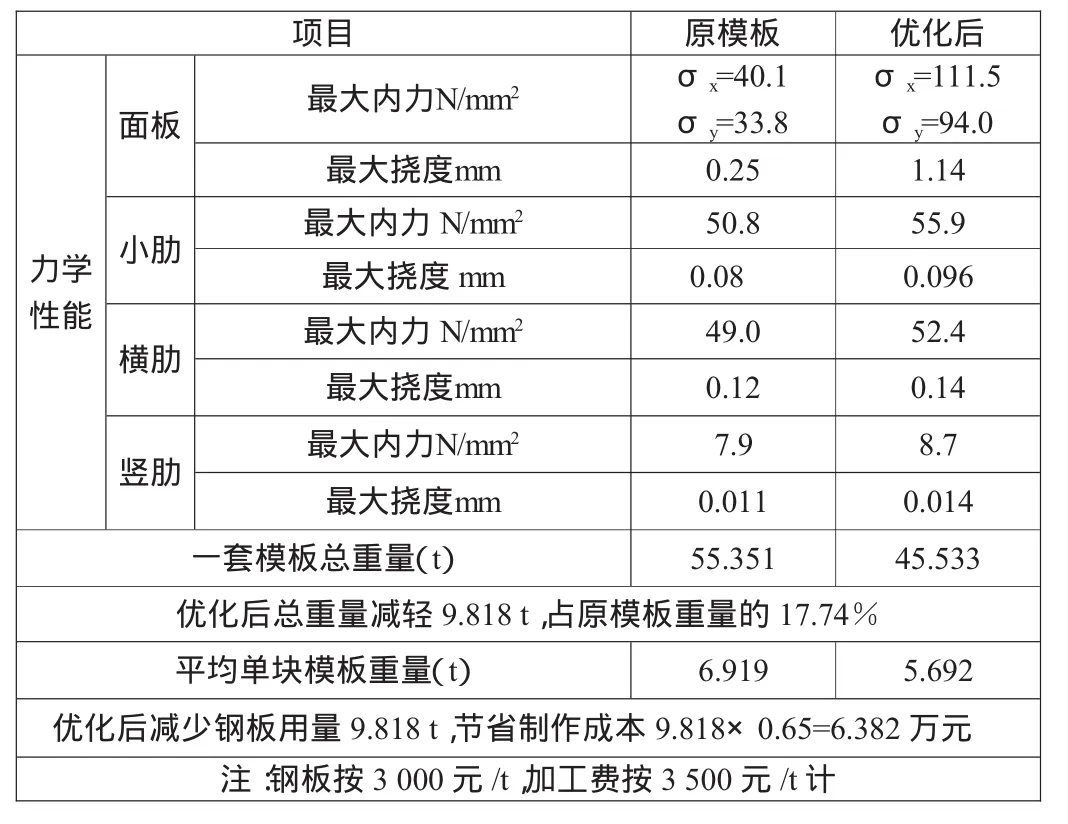
表1 优化前后对比见表