均生函数逐步回归模型在水文长期预报中的应用

冯 健，张常俊

（黑龙江省水文局，黑龙江 哈尔滨 150001）

水文要素可以看作是一个随机过程，但其自身往往具有一定的周期规律，影响水文长期预报的因素极其复杂，当我们难以找到与预测要素关系密切的影响因子时，利用预测要素自身历史资料的变化规律来预测未来一段时间该要素的状况就是一种较为有效的方法。

一般时间序列预测模型的预测结果往往趋近于平均值，而对极值的拟合效果欠佳，根据水文时间序列蕴含不同时间尺度的震荡特征，均生函数模型做多步预测，弥补了其他时间序列模型的缺陷，对序列极值的拟合和预测会得到比较理想的效果。

1 模型原理与构建

设时间序列为 X（t），（t=1，2，…，N）构造均生函数：

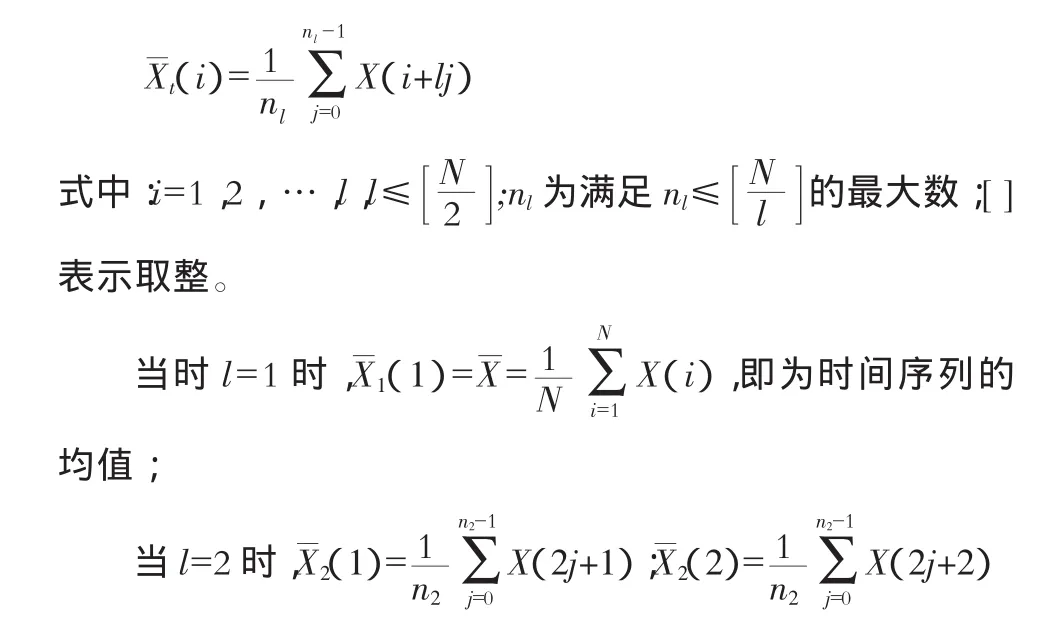
类似的有X3（i），X4（i），…，XL（i），由此可以得到一个下三角矩阵：

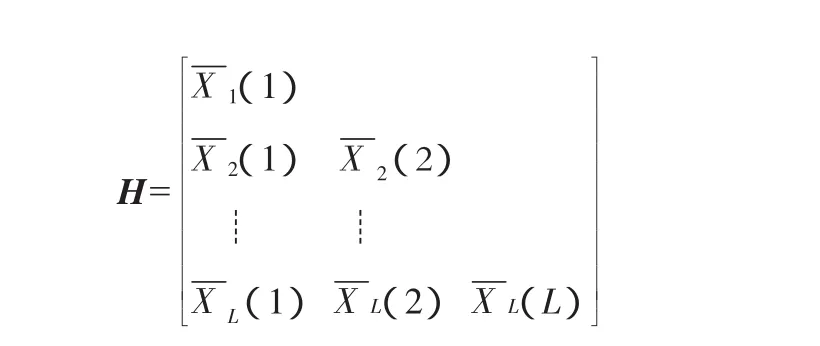
称H为l阶均生矩阵，在此不对求平均值的样本大小做严格限制，只要求至少有2个数据求平均，于是L=lmax=对（i）作周期外延，即：

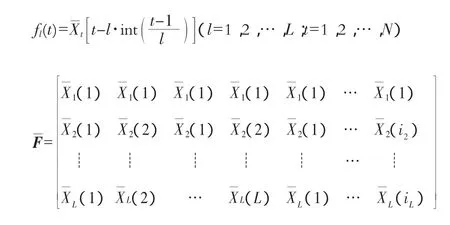
由此构造出均生函数的外延矩阵如下：

所以得到了f（1t），f（2t），…，f（Lt）等]个预报因子系列。将f（it）作为预报因子，X（t）作为预报对象，进行多元逐步回归，建立多元回归模型进行预测，即：

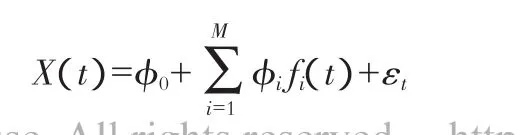
2 实例计算

2.1 资料选取

自1953年至2009年共57年资料，其中1953—2000年作为回归建模拟合，2001—2009年资料作为预测检验。

2.2 分析计算

运用自编程序对江桥1953—2000年流量年极大值系列进行处理运算，生成24个均生函数系列，选择信度α＝0.05，将生成的均生函数系列作为预报因子与极值系列作逐步回归分析，从中选出合适的因子并建立多元回归模型，得到的回归方程如下：

X（t）＝0.729f2（1t）+0.773f2（2t）-2 143.94

回归方程的确定性系数为0.60，复相关系数为0.78，检验情况如下：

由于F＝34.31＞F0.05＝3.2，各回归系数为零的假设不成立，回归效果是显著的。

由于 t＝8.29＞t0.05/2＝2.01，全部随机自变量与因变量是线性相关的。

将各因子值带入回归方程，发现拟合情况还是不错的，拟合情况如图1所示。

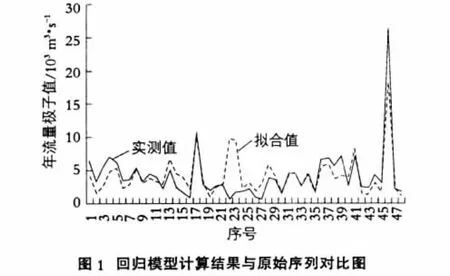
2.3 模型检验

将均生函数因子系列外延9年，带入回归模型方程，预测出2001—2009年的年最大流量，按照水文情报预报规范对预测的极值进行精度检验，我们发现，其合格率还是比较高的，9年检验期，有6年是合格的，合格率达到67%。检验情况见表1。

表1 误差精度检验统计表

3 结语

对单一要素序列求均生函数，生成包含不同预报信息的多个预报因子序列，通过逐步回归确定关系密切的预报因子，得到回归方程后，就可建立具有多步预测的模型。

通过对嫩江江桥站的多步模拟分析，结果表明，在不要求十分精细的预报时，运用均生函数模型预测对水文长期预报还是具有很好的参考作用的。

均生函数模型假定事物的过去趋势会延伸到未来，而随着人类改变自然能力的提高，自然环境的变化本身也对水文规律造成了影响，如尼尔基水库等对江桥站的规律影响就是十分明显的，其自身的规律可能发生了变化。

本文均生函数因子序列生成及逐步回归均采用计算机程序自动计算，经多次检验，可靠性很好，省去了人工计算的大量工作并避免错误的发生。

［1］汤成友，官学文，张世明.现代中长期水文预报方法及其应用［M］.北京：中国水利水电出版社，2008.

［2］袁本荷.利用均生函数预测模型作降水预报［J］.四川气象，2005，25（3）：8-9.

［3］杨瑞峰，刘庆民.均生函数模型在长期天气预报中的应用［J］.河南气象，2004（1）：23-24.

［4］覃志年，均生函数逐步回归模型在降温、降水长期过程预测中的应用［J］.广西气象，2003，24（1）：15-17.