大型船舶推进轴系回旋振动特性分析研究
2010-04-01谢俊超周瑞平
王 磊,谢俊超,周瑞平
(武汉理工大学能源与动力学院,湖北武汉 430063)
0 引言
船舶推进轴系作为一种转子系统,影响其振动特性的因素较多。除轴系本体的结构对振动特性有较大影响外,系统中其他因素对回旋振动特性也有不同程度的影响,如轴承支承点位置、轴系校中状态、支承系统特性、密封装置等[1]。此外,船舶推进轴系周围介质对回旋振动也有影响,如附连水效应[1]。对以上因素,已有不少文献进行了专门的研究,得到一些较为成熟的理论。但是,对于陀螺效应(主要是螺旋桨的陀螺效应)、应力刚化及旋转软化效应研究较少,在计算中也未做考虑。
本文在深入分析低速转子系统动力特性的基础上,研究了陀螺效应、应力刚化及旋转软化效应对船舶推进轴系回旋振动特性的影响,并以某VLCC船轴系为实例,利用通用有限元分析软件进行建模计算,分析了螺旋桨惯性力矩,即陀螺力矩、应力刚化及旋转软化效应对回旋振动计算的影响。
1 模型建立
对于大型船舶推进轴系,运用有限元方法进行振动计算具有明显的优越性。为了分析的方便,本文以某VLCC船轴系为实例进行建模计算,推进轴系简图如图 1所示。该船为299 500DWT油船,全长320m;螺旋桨为4叶定距桨,其直径是10m,干重73 844kg。
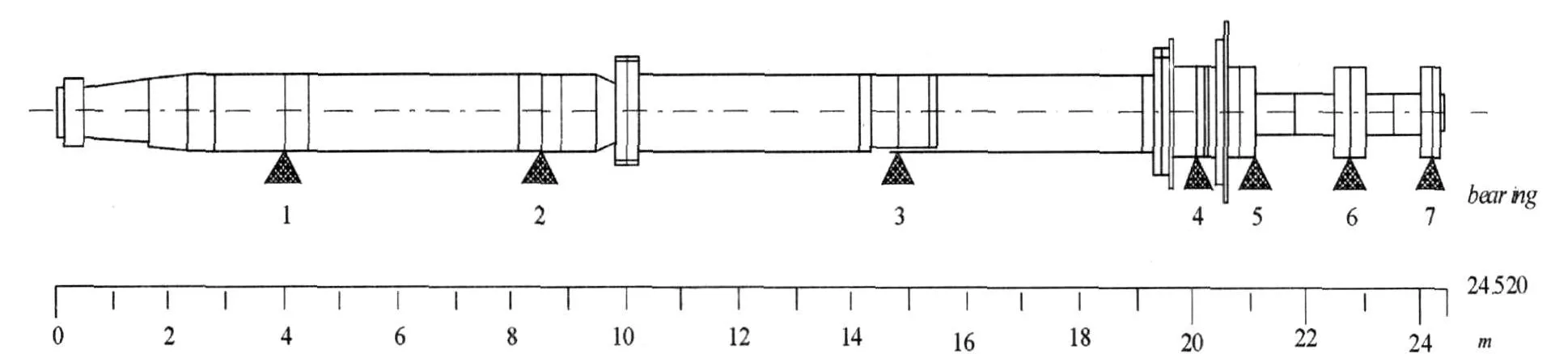
图1 某VLCC船推进轴系简图
在建模时为很好地模拟大型船舶推进轴系的状态,并考虑轴段的应力刚化及旋转软化效应,选用Beam4梁单元进行模拟,但Beam4梁单元截面显示效果较差。
对于螺旋桨,因其结构复杂,在结构参数缺乏的情况下难于建立精确的实体模型,故采用Beam4梁单元建立圆盘来简化模拟,并根据等效前后质量和转动惯量一致的原则,确定该圆盘的长度和截面直径。这样,可较精确地模拟实体螺旋桨的回转效应。有限元模型中圆盘作用点位置与实体螺旋桨作用点一致。
对于弹性支承系统的轴承采用Combine14弹簧单元进行模拟,在每个支承位置的垂向和横向分别设置一个弹簧单元来模拟轴承部分在 y方向和z方向的弹性。根据回旋振动的特点,将接地端设为固定端,并限定支承位置节点 x方向平动自由度以消除纵向振动模态的影响。因为假定轴承各向刚度相等,故可仅保留y方向平动自由度及 z方向旋转自由度。
通过以上简化处理并进行相应设置得到其有限元模型,如图 2所示。
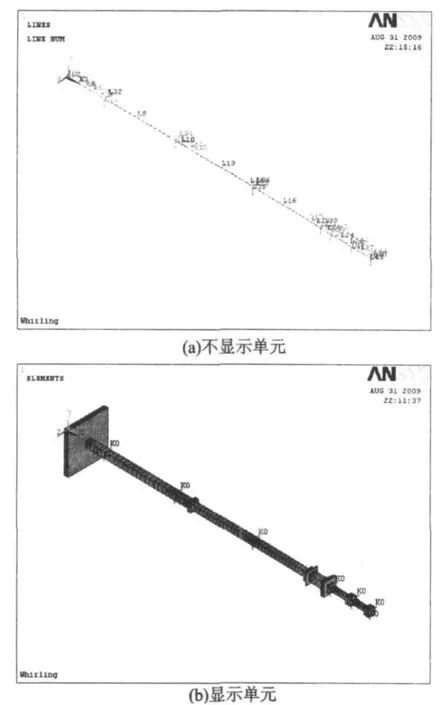
图2 轴系振动分析有限元模型
2 陀螺效应影响分析
2.1 螺旋桨陀螺效应
船舶推进轴系的尾部是一带有巨大螺旋桨的悬臂端,当轴系作回旋振动时,螺旋桨轴中心线在空间的轨迹是一个以 x轴为对称轴的圆锥面或椭圆锥面,螺旋桨盘面将随转轴的回旋产生偏摆,螺旋桨的动量矩矢量的方向将不断变化。此时,螺旋桨对转轴除有惯性力作用外,还有惯性力矩(即陀螺力矩)的作用。
现假定支承刚度各向相同,并假定螺旋桨无偏心质量。将螺旋桨简化为一等效刚性匀质薄圆盘,转轴简化为一无质量弹性轴[2]。如图 3所示,轴系回旋振动时的运动可分解为:其绕自身几何线中心OC旋转的自转和几何中心线绕支承中心线OA旋转的公转(进动或称涡动)。在圆盘或转轴中心线上任一点的绝对角速度 ω等于自转角速度 ωs和回旋角速度Ω的矢量和,即ω=ωs+Ω;圆盘总的动量矩L是圆盘在切线方向的动量矩 Lt与法线方向的动量矩Ln之和,即L=Lt+Ln。其中:
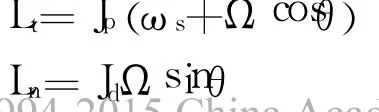
式中:Jp和Jd分别为螺旋桨的极转动惯量和径向转动惯量。

图3 螺旋桨回转效应示意图
为求出陀螺力矩的大小,将L分解为x轴方向与垂直于x轴方向的动量矩Lx、Lr,表达式为:
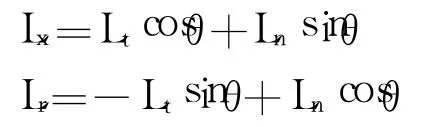
稳定运转时,Lx的大小与方向均不变化,Lr的大小不变,方向则按回旋角速度Ω在垂直于x轴的平面内旋转。这里外力矩是转轴作用于圆盘的力矩M′g,螺旋桨圆盘作用于转轴的惯性力矩 Mg的大小与M′g相等,方向相反。其表达式为:

式中:j0为转动惯量比,j0=Jp/Jd;h为频率比,h= ω/Ω。
可知,陀螺力矩包含 2项:JpωΩθ为哥氏惯性力矩;另一项 JdΩ2θ为牵连惯性力矩。
轴系的陀螺力矩为正值时,阻碍轴的弯曲变形,相当于增加了轴的弯曲刚度,使轴系的固有频率增加。反之,则使轴系的固有振动频率下降。
轴段的陀螺效应对固有频率的影响很小,不具有实际意义,可以忽略不计。
2.2 考虑陀螺效应的有限元计算
传统的转子动力学分析采用传递矩阵方法进行计算,由于将大量的结构信息简化为极为简单的集中质量 -轴段等模型,不能确保模型的完整性和分析的准确度;而利用有限元方法处理时,可以很好地兼顾模型的完整性和计算的效率。但多年来,转子的“陀螺效应”一直是制约转子动力学有限元分析的“瓶颈”问题。ANSYS很好地解决了动力特性分析中“陀螺效应”影响的问题,而且陀螺效应的考虑不受模型上的限制,使得转子动力学有限元分析变得简单高效。
当考虑转子的陀螺效应时,系统的运动方程中会出现一个反对称的陀螺矩阵。一般情况下,静止坐标系下考虑陀螺效应的转子系统运动微分方程式可写为
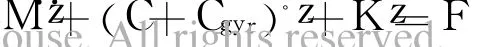
式中:Cgyr是陀螺矩阵,反对称阵。在旋转坐标系下考虑陀螺效应的转子系统运动微分方程式写为:

式中:Ccor是哥氏效应矩阵;Kspin是旋转软化效应刚度矩阵。
对于轴系回旋振动的总参数元件 -分布参数元件混合系统动力学分析模型也可考虑螺旋桨(圆盘)的陀螺效应,但此时圆盘的传递矩阵将有所不同,计算结果亦将不同,但结果遵循相同趋势。
对上述实例进行考虑陀螺效应的回旋振动有限元计算,结果见表 1。陀螺效应对回旋振动的影响见图4。
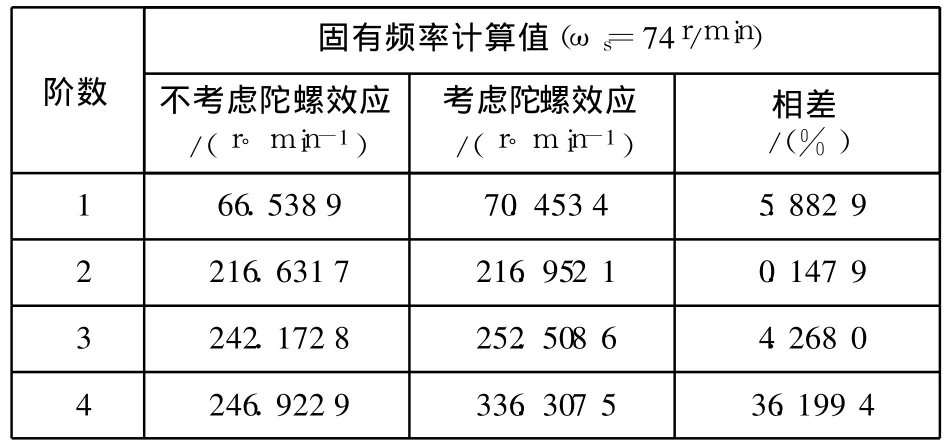
表1 螺旋桨陀螺效应对固有频率的影响
从表 1可以看出,其计算结果与前述理论分析相一致,即当轴系(主要是螺旋桨)的陀螺力矩为正值时,使轴系的固有频率增加。而且,陀螺效应还与轴系工作转速有关,工作转速增大,陀螺效应相应增强,对轴系回旋振动固有频率的影响加剧。一般来说,桨的转动惯量和轴的角速度之乘积愈大,其影响也愈大,这一点可从上述哥氏效应力矩的表达式中看出。此外,由于船舶轴系转速特性与高速转子系统的差异,其牵连惯性力矩一般是不能忽略的。
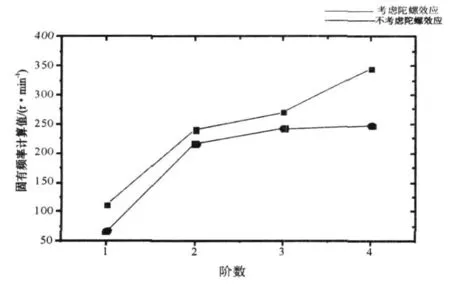
图4 陀螺效应对回旋振动的影响
3 应力刚化及旋转软化效应影响分析
3.1 应力刚化及旋转软化效应的理论基础及其影响
结构的面外刚度可能大大地受结构中面内应力状态的影响。面内应力和横向刚度之间的耦合即为应力刚化。因此,当结构体的弯曲刚度相对其轴向刚度较小时,一般需考虑应力刚化效应,如线缆、薄壳或叶片状结构物。其结果是离心力产生的张应力使垂直于张应力方向的结构刚度增加[3]。
对船舶推进轴系来说,应力刚化效应的直接影响是使螺旋桨叶片的弯曲刚度增大,并因此造成系统的固有频率增高。
通常考虑离心惯性力的螺旋桨叶片动力学方程可表为M¨z+Cz˙+Kz=F,式中总体质量矩阵(M)、总体阻尼矩阵(C)、总体刚度矩阵(K)及总体载荷向量(F)分别由单元质量矩阵、单元阻尼矩阵、综合单元刚度矩阵及综合单元外载向量组集而成。
由于正常工作时螺旋桨内部应力大小仅与外载有关,并与外载成正比,而与材料常数无关。因此,船舶推进轴系应力刚度也只与外载即离心惯性力有关,并与离心惯性力成正比,而与材料常数无关。又由于离心惯性力与轴系转速 ω的平方成正比,因此应力刚度也与轴系转速的平方成正比。
如忽略阻尼力的影响,并令总体载荷向量 F= 0,得到考虑离心惯性力的轴系振动方程M¨z+Kz= 0,其与船舶推进轴系的自由振动方程在形式上是一样的,但其中的总体刚度矩阵是由综合单元刚度矩阵组集而成,而综合单元刚度矩阵则是由结构单元刚度矩阵与应力单元刚度矩阵两部分组成。
旋转软化是指动态质量效应调整(软化)旋转物体的刚度矩阵。在小位移分析中这种调整近似于大的环形运动而导致几何形状改变的效应。旋转软化对船舶推进轴系回旋振动也有一定程度的影响。其力学性质为:在对这类线性问题进行模态分析的解算时,考虑大变形几何非线性的影响。
如图5所示为一简单弹簧 -质量旋转系统。
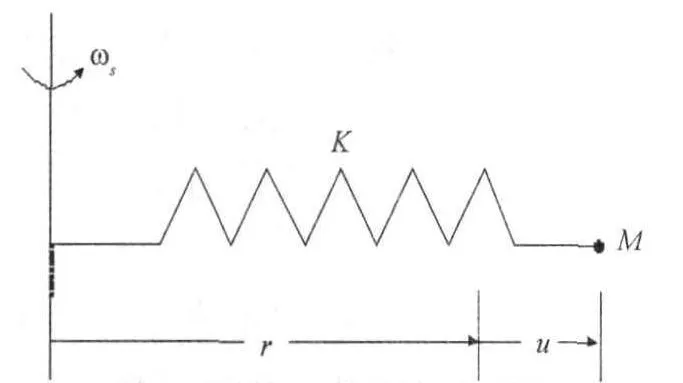
图5 弹簧—质量旋转系统
当基于小变形理论时,系统的平衡方程为Ku= Mω2sr,式中K为弹簧刚度,u为相对自由位置质点的位移,M为质点质量,ωs为旋转角速度,r为质点的自由位置相对转轴的半径[4,5]。
当考虑大变形效应时,系统的平衡方程应为:
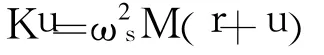
移项后变换为:

定义:

则平衡方程式可表示为:
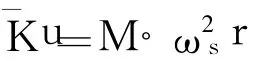
3.2 应力刚化及旋转软化效应的有限元处理
ANSYS中通过生成和使用一个称作“应力刚化矩阵”的辅助刚度矩阵来考虑应力刚化效应。尽管应力刚度矩阵是使用线性理论得到的,但由于应力(应力刚度矩阵)在每次迭代之间是变化的,因而它是非线性的、而旋转软化效应通常和预应力一起使用,这种预应力由旋转物体中的离心力所产生,它不应和其他变形非线性、大挠度和大应变一起使用。对上述实例,考虑应力刚化及旋转软化效应情况下有限元计算结果见表 2。
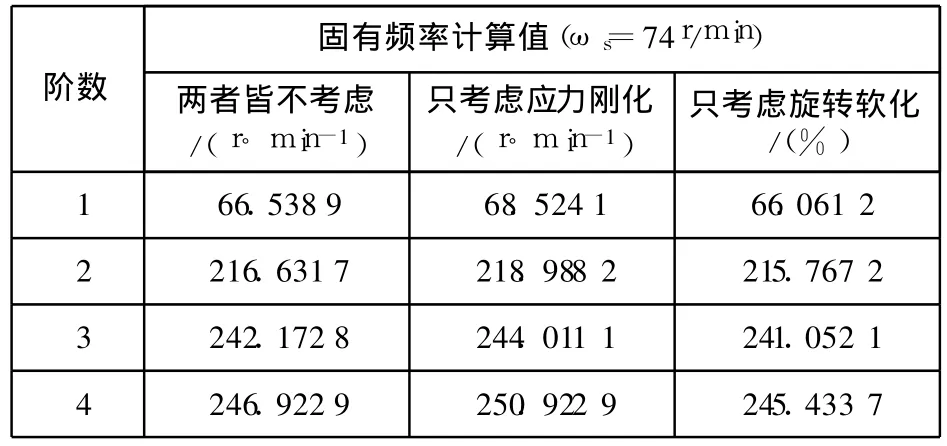
表2 应力刚化效应及旋转软化效应的影响
应力刚化效应及旋转软化效应对固有频率的影响如图 6所示。从图 6可知,低速时应力刚化和旋转软化效应都不明显,转速逐渐升高时应力刚化和旋转软化效应愈加明显;与应力刚化相比,旋转软化对船舶推进轴系模态特性的影响较小;应力刚化和旋转软化对船舶推进轴系模态特性影响不大,一定程度上可忽略。
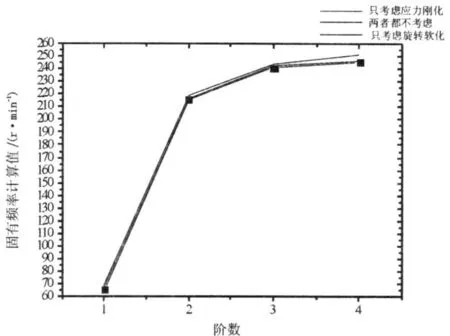
图6 应力刚化效应及旋转软化效应对固有频率的影响
4 结论
本文以转子动力学理论为基础,并综合考虑船舶推进轴系的动力学特性,建立了船舶推进轴系的有限元计算模型,从理论上给出了陀螺效应、应力刚化及旋转软化效应对船舶推进轴系回旋振动特性的影响趋势,并使用有限元分析软件进行详细计算分析,验证了理论分析的结果,并得出这三个效应对大型船舶推进轴系的具体影响,对大型船舶推进轴系的设计具有指导意义。
[1] 周瑞平.基于VB的船舶轴系回旋振动计算软件[J].造船技术,1999,(3):1-4.
[2] 陈之炎.船舶推进轴系振动[M].上海:上海交通大学出版社, 1987.
[3] 王小立.船舶推进轴系动态性能分析与研究[D].武汉:武汉理工大学,2008.
[4] 廖日东,左正兴,陈宏,等.考虑旋转软化效应的涡轮叶片模态特性研究[J].内燃机学报,2000,18(3):1-4.
