扭矩测量系统变差分析初探
2010-03-28
(潍柴动力股份有限公司,潍坊261001)
扭矩测量系统变差分析初探
赵庶娴,李效伟,鞠录梅,卢景芳
(潍柴动力股份有限公司,潍坊261001)
介绍了扭矩测量系统偏倚分析的具体运作方法,并通过柴油机螺栓拧紧扭矩测量系统实际案例,详细阐述了样本选择、原始数据的采集及数据的计算与分析等。
测量系统分析扭矩测量系统偏倚分析t统计量显著性检验
1 前言
随着TS 16949在汽车零部件制造业中的普及运行,作为其中五大工具之一的MSA也得到了越来越深入的研究,研究对象从开始的简单测量系统逐渐向复杂测量系统过渡,覆盖过程从加工过程延伸到总装试车过程,测量项目从几何量检测扩展到零部件机械性能测试乃至整机性能评定等等。
发动机制造业中最常见的复杂测量系统主要包括两大类:一类是以关键零部件的硬度检测、拉伸试验为代表的破坏性测量系统;另一类是柴油机总装线上主轴承、连杆等关键零部件的螺栓拧紧过程,即不可重复的扭矩测量系统。这两类过程在工艺控制中属于最终工序或关键过程,对产品性能有着直接关系,所以对其进行测量系统分析(MSA, MeasurementSystem Analysis)是非常必要的。而复杂测量系统分析与简单测量系统分析相比,不仅是方法选择的区别,而且还包括样本的选择方式、数据的采集方式、原始数据的计算与分析方式等等,其具体实施的各方面均有很大的不同。以下将以实例对不可重复的扭矩测量系统的变差分析进行具体说明。
2 扭矩测量系统的变差分析
以连杆螺栓拧紧过程为例用偏倚分析的方法对扭矩测量系统的变差进行研究。
偏倚(Bias):是指对相同零件上同一特性的观测平均值与真值(参考值)的差异。
2.1 测量系统概述
本过程中所用测量设备(同时也是生产设备)为QMX62-32RT两轴连杆螺栓拧紧机,相关零部件为连杆总成及连杆螺栓。工艺参数要求最终扭矩应控制在150~250N·m之间。
2.2 样本的选择
在测量系统分析参考手册中[1],确定测量系统偏倚时采用的是独立样件法,即取得一个样件,并且建立其可追溯到相关标准的参考值(此参考值可通过高一级精度测量设备检测得出)。然后由评价人以正常方式测量样件≥10次,对采集的数值进行偏倚分析。这对于简单测量系统是很容易做到的。
而扭矩测量的不可重复性,决定不可能采用简单意义上的“独立样件”。在这种情况下,可依据MSA参考手册的提议,从稳定过程的大量样本中(大于30)选择具备统计上的一致性的个样本,将其收集隔离为“独立样件群”,整体作为一个广义上的“独立样件”参与数据分析。此处需要说明一下,拧紧过程的样本件应是成对的,如连杆体和螺栓。
为保证样本的一致性,取样时可从以下几个方面进行考虑:
(1)为减少样本选择过程的变差,整个取样过程最好是一次性完成。
(2)保证所有样件均来自同一台生产加工设备的连续生产过程,并具有相同的操作者、相同的原材料、相同的生产环境等。
(3)对样件的相关属性,即可能影响拧紧过程的各项特性值(如:螺纹中径、螺距、牙型半角、材质、机械性能等)进行检测,并剔除异常产品,同时通过检测数据对过程能力进行研究,确定其总变差为可接受,即生产过程是稳定过程,使被选样本真正具备统计意义上的一致性。
(4)样本挑选完毕后要妥善保存,保证这批样本在预期评价周期内其被测特性不会发生改变(如有发生改变的样本必须剔除)。
(5)一般需保证有15至20对备选样本。
2.3 数据的采集
本例中实际选取15对连杆体和螺栓作为样本,分别由拧紧机(经校准其示值误差为3%)按工艺设定值对连杆螺栓进行拧紧。保存拧紧机同步显示的动态扭矩值,记录为实际观测值;然后由评价人再使用高精度数显扭矩扳手(经校准其示值误差为2%)对拧紧后的螺栓进行静态校验,此次显示的扭矩值为对应的参考值,并记录为参考观测值X,参见表1。如此共进行15组数据的测试,计算出每一组的差值作为偏倚进行统计分析。
2.4 图示法分析
依据计算得出的偏倚值及其分布频率画出直方图,如图1所示。从直方图上可以看出,此分布没有明显的偏峰和陡壁,中心线与0线接近,基本近似正态分布,由此判定测量过程没有特殊原因造成的异常点出现,可以进行下一步的分析。
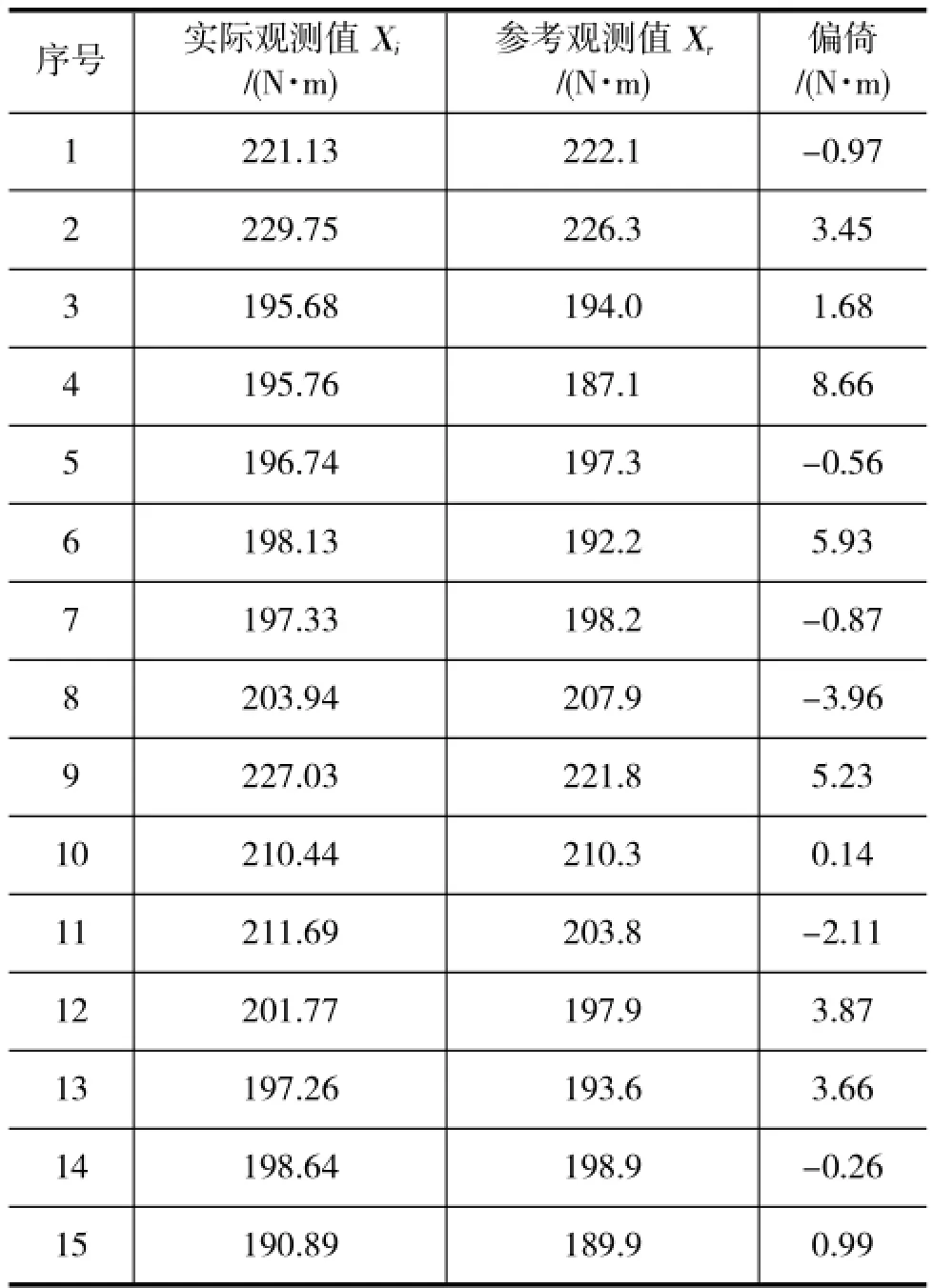
表1 连杆螺栓
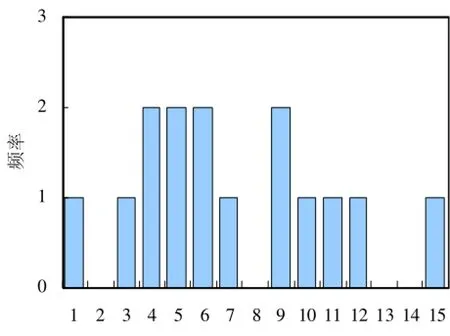
图1 偏倚直方图
2.5 数值法分析
将得到的15组数据汇于表1后按测量系统分析参考手册的要求进行分步计算:
(1)计算参考值
以高精度数显扭矩扳手采集的静态校验值的均值作为参考值,即:

(2)计算拧紧机显示的观测平均值
以拧紧机显示的动态扭矩值的均值作为观测平均值,即:
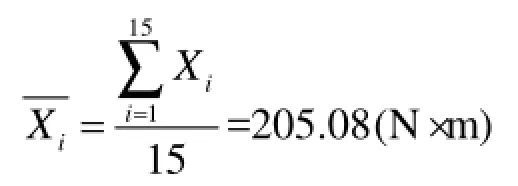
(3)利用极差法计算观测值的标准差
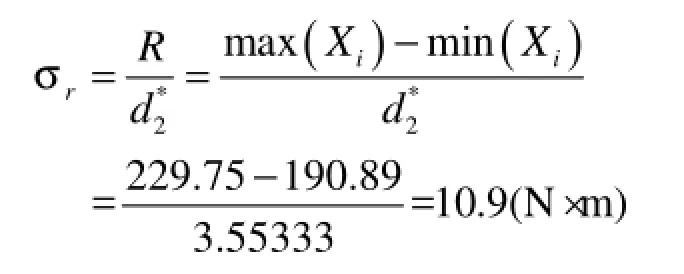
(4)计算平均值的标准差:

(5)计算偏倚:

(6)确定统计量:

(7)利用假设检验进行判断
小样本(容量小于30)检验宜选用检验。
H0假设:0落在偏倚值附近的1-的置信区间内,则偏倚在水平上是可接受的。
取=0.05(即预设置信水平为参考手册默认的95%,若要改变水平值,应该事先得到用户的同意)。
本例中测量零件的次数为=15次,作为一个子组处理(即=1),因此该子组的大小(也叫子组容量)==15。根据=1和=15,可从参考文献[1]的附录-2*表中查得“与平均极差的分布有关的数值”:自由度=10.8。
由=10.8和=0.05查标准分布表:
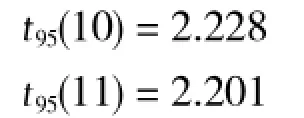
因计算的统计量小于的显著值,故在显著性水平0.05上接受0假设,即可以初步判断被测样本间无显著性差异。
第二步,计算置信区间:
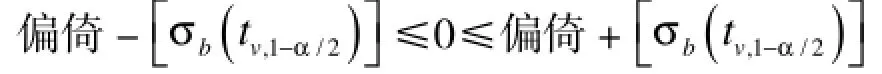
查文献[1]附录-2*表,当=1和=15时,查得2*=3.553,同时可查得2*的无限值2= 3.472。
因2是2*的无限值,即最终收敛值,所以在实际分析过程中常用以下公式替代原公式,计算其置信区间:

由以上计算结果可以看出,0落在偏倚置信区间的上限和下限之内,因此不能拒绝0假设,即这个测量系统的偏倚在95%的置信水平上不存在显著差异,是可以接受的。换言之,此拧紧过程中,测量系统的偏倚将不会带来额外的变差(Variation)来源。
3 结论
本文主要是采用偏倚分析的方法对扭矩测量系统进行变差分析。而在日常过程控制中,除了对重要测量系统进行必要的变差分析以外,还应该对其进行长期的稳定性分析,保证过程的持续有效。
1 AIAG.Measurement Systems Analysis(MSA)ReferenceManual(3rd edition),中国汽车技术研究中心编译.2002.
Preliminary Studiesof TorqueMeasurementSystem Variation
Zhao Shuxian,LiXiaowei,Ju Lumei,Lu Jingfang
(WeichaiPower Co.,Ltd.,Weifang261001,China)
A specific operation ofbias analysis of torquemeasurementsystem is introduced with a real case of engine bolts tightening.It includes in details samples selection,original data collection,calculation and analysisetc.
measurement system analysis,torque measurement system,bias analysis,t-statistic,test of significance
10.3969/j.issn.1671-0614.2010.04.010
来稿日期:2010-06-07
赵庶娴(1971-),女,高级工程师,主要研究方向为测量过程控制、测量系统分析及测量不确定评定。
