多自由度平台微振动LQG最优控制

周晓宏

（深圳职业技术学院电子与信息工程学院，广东 深圳 518055）

随着科学技术的快速发展，当今世界的机械加工已迈入超精密时代。同时，高精密仪器设备也在不断涌现。高科技设备诸如激光、光学仪器和集成电路生产设备，由于对工作环境中的各种微振动十分敏感，并且其造价昂贵，因而有必要对设备周围的微振动干扰进行隔离和控制。

高精密仪器微振动隔振平台系统设计，一般需要考虑各种复杂的环境微振动干扰，主要有来自轨道交通车辆行驶引起的地面振动、台面试验仪器引发的干扰以及直接干扰[1]。环境微振动干扰主要包括：大地脉动型地面振动频率主要在0～1 Hz；房屋骨架、墙壁和地板一般易在15～25Hz产生与剪切和弯曲有关的振动；办公室工作人员走动，会引起频率在1～3 Hz的振动；通风管道、变压器和发动机所引发的振动在6～65 Hz之间，建筑物自身的振动一般在10～100Hz之间[2]。

在微振动隔振系统设计时，往往需要考虑频率范围为0～100 Hz的微振动。这就要求设计的隔振系统，需要对中高频干扰，如高精密仪器的运转、轨道交通的行驶、以及人员走动等引起的地面振动等，具有良好的隔振效果；而且对低频和超低频干扰力，如由周围声音、空调气流等引起的作用于平台的压力，也能进行有效的隔离[3]。

因此，笔者采用被动隔振与主动隔振相结合的混合隔振技术，建立了多自由度平台系统的结构模型，并采用LQG最优控制理论设计了控制器，在基础干扰和直接干扰下，平台在X、Y、Z方向的位移时程和速度时程，取得了明显的控制效果。

1 多自由度平台的结构模型

设计的多自由度微振动混合隔振系统结构平台尺寸，为长 2000mm、宽 1500mm、高 250mm，总质量为 2000 kg，平台上允许操作荷载2000 kg。该系统主要包含有1个平板、8个超磁致伸缩致动器、5个空气弹簧。4个超磁致伸缩致动器水平放置（两个在x方向，两个在y方向），另外4个超磁致伸缩致动器垂直放置在4个角落，5个空气弹簧垂直分别放置在4个角落和平板几何中心。

将平台的运动视为一刚体，因而其运动可以被简化为一个六自由度系统。6个变量分别是：平台重心G在X，Y，Z方向的3个平动位移（xG，yG和 zG）；绕 X，Y，Z轴的 3个转角位移（θx，θy和 θz）。用 X，Y，Z 方向的弹性元件（kxi，kyi和 kzi，i=1～5）和阻尼元件（cxi，cyi和 czi，i=1～5）作为空气弹簧的理论分析模型。

则多自由度平台系统的运动微分方程可表述如下：

其中，

[M]为质量矩阵；

[K]为刚度矩阵；

[C]阻尼矩阵；

Ka为超磁致伸缩致动器输出力因子矩阵。

为了便于计算，需要对上面的运动微分方程进行简化。首先对系统做如下假定：

（1）5个空气弹簧的性能和尺寸完全一样，每个空气弹簧的垂直刚度均为kV，水平刚度（X，Y）均为kH；每个空气弹簧的垂直方向阻尼均为cV，水平方向阻尼（X，Y）均为cH。

（2）L3=0.25 L2。

2 LQG最优控制系统的设计

考虑系统随机输入噪声与随机量测噪声的线性二次型最优控制叫做线性二次型Gauss（LQG）最优控制。这是一种输出反馈控制，对解决线性二次型最优控制问题，更具有实用性。

多自由度平台系统的运动微分方程可表述为如下的状态方程：其

ω(t)和 ε(t)为白噪声信号；

ω(t)为系统干扰噪声；

ε(t)为传感器带来的量测噪声。

假设这些信号为零均值的 Gauss过程（E（ω）=E（ε）=0），

其协方差矩阵分别为

进一步，假设ω(t)和ε(t)为相互独立的随机变量，则

由此，最优控制的目标函数定义为

3 平台整体六个自由度的振动控制仿真

选状态变量为

其中，

[M]为质量矩阵；

[K]为刚度矩阵；

[C]为阻尼矩阵；

[Ka]为控制力输出因子矩阵。

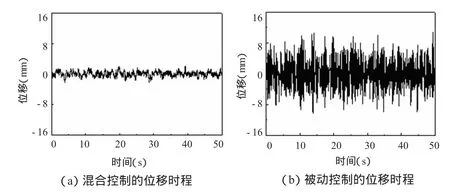
图1 在基础干扰和直接干扰下X方向被动控制和混合控制的位移时程

图1为在基础干扰和直接干扰下共同作用时，被动控制和主动控制的X方向位移时程，将两者的位移结果对比得出：混合控制下X方向的位移均方根值为被动控制的18.29%。

图2为被动控制和主动控制的速度时程，将两者的结果对比得出：混合控制下平台X方向速度均方根值为被动控制的22.57%。

图2 在基础干扰和直接干扰下X方向被动控制和混合控制的速度时程

5 结束语

本文采用被动控制与主动控制相结合的混合控制技术，建立了多自由度平台系统的结构模型，该系统以空气弹簧作为被动隔振元件，超磁致伸缩制动器为主动隔振元件。并建立了多自由度混合隔振系统的动力学模型，利用LQG最优控制理论设计控制器。利用DSPACE系统在MATLAB中用simulink进行的仿真研究表明，所设计的LQG最优控制器，可对基础干扰和直接干扰所引起的微振动进行有效地控制，其振动效果明显优于被动控制。

[1]Ungar EE，Sturz DH，Amick CH.Vibration Control Design of High-Technology Facilities[J].Sound and Vibration，1990，（24）：20-27,

[2]Nakamura Y，Najayama M，Masuda K，Yasuda M，Fujita T.Development of 6-DOF Microvibration Control System Using Giant Magnetostric tive Actuator[J].Proceedings of SPIE Conference on Smart Materials and Smart Structures,Newport Beach,CA,U.S.A.,1999，（3671）：229-240.

[3]张春良，梅庆德，陈子辰.微制造平台微振动的H2/H∞混合控制[J].仪器仪表学报，2004，25(3):298-301。

[4]飞思科技产品中心.Matlab 7辅助控制系统设计与仿真[M].北京：电子工业出版社，2005.