机载双天线干涉SAR非线性近似自配准成像算法

陈立福 韦立登 向茂生 韩松涛

①(中国科学院电子学研究所 北京 100190)②(中国科学院研究生院 北京 100039)

1 引言

干涉合成孔径雷达(InSAR)技术是在合成孔径雷达技术基础上发展起来的，是射电天文学干涉测量技术与合成孔径雷达技术的结合。它采用两副天线同时对地观测(单轨模式)或一副天线两次近似平行观测(重轨模式)方式，来对观测场景分别成像并利用两副图像产生干涉相位，最后利用两天线几何关系及干涉相位来提取地表数字高程模型(DEM)。

要获得高精度DEM，精确的干涉相位的产生至关重要。而在实际的干涉系统中，系统热噪声、图像失配以及时间去相关等都会造成干涉相位误差。而其中的图像失配更是一个重要的影响因素，因此图像配准是一个重要的干涉处理环节。现有的配准算法主要从两个方面进行配准[1,2]：一种是从得到的两幅SAR图像的相关性上去配准，该配准方法是通过一种准则来判断两幅图像的相关程度进行配准，如相关函数法、最大干涉频谱法、相位差影像平均波动函数法等；另一种是从几何特征上去配准，首先采用一些准则从图像中提取特征点，进而找出在主辅图像中该点的对应坐标来进行配准。前一种方法的稳定性和准确性较好，但计算量巨大；后一种方法的计算量较前一种小些，但该类方法在提取特征点时往往会有度量准则的平滑连贯性不好以及配准的鲁棒性不好的问题[1]。还有些方法将一些辅助信息(如外部DEM)加入传统配准算法中来进行更高精度的配准[3]。这些配准算法都是基于得到SAR图像后的配准，计算量均较大。文献[4]中曾提到距离向变标原理可用于干涉图像对的距离向配准，但并未深入分析；文献[5]中给出了线性近似的ECS自配准算法，该算法运算量较小，但配准精度不高。

为满足高精度DEM和实时干涉，本文采用非线性近似ECS自配准成像算法，在SAR成像处理过程中实现高精度距离向自配准。而仿真结果证明了该算法在配准精度上较线性自配准有很大提高，且基本没增加计算量，非常适于实时干涉处理。

2 干涉SAR信号回波模型

图1给出了系统干涉几何关系图，H为载机高度，By和Bh是基线在垂直飞行方向的水平和竖直分量，B为基线长度，α为基线倾角，β为地面坡度。P(x, y, z)为观测区域内一目标点，θ1为天线A1到该点视角，r0为目标到天线A1航迹垂直距离，h为目标的相对高度，y为目标距离天线A1的水平距离。

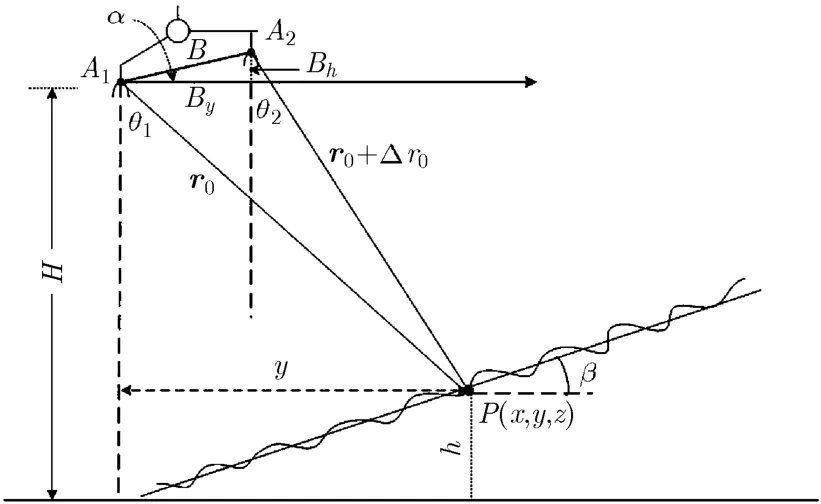
图1 干涉几何图

在实际系统中，为了降低采样率，经过混频和正交通道分离把接收信号变为复基带信号。设接收到的回波经解调后点散射体的时域响应为

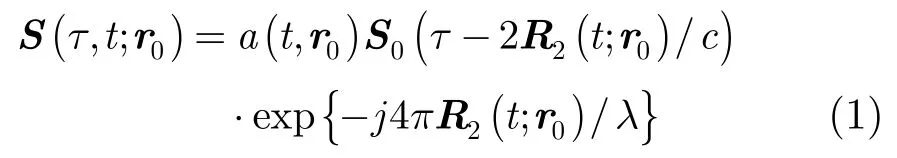
其中a(t, r0)为天线加权，S0为接收的信号包络，t为平台飞行时间，λ为波长，τ是接收回波的距离向延迟时间，c为光速，R2(t;r0)为信号从发射到接收过程中A2到散射体距离(正侧视)，其表达式如下：

设SAR一般发射的线性调频信号为

其中T为持续时间，fc是中心频率(在接收信号时已经被调制到基带)，Kr为调频率。

将线性调频信号考虑进回波模型，则式(1)变为

[4,6]可得式(4)距离多普勒域信号为

其中ft为方位向频率，A(τ,ft;r0)和S0(τ,ft;r0)为距离多普勒域天线加权和信号包络，rref为参考位置(一般为场景中心)到A1的距离，弯曲因子为β(ft)=KS为参考距离处的有效调频率其中R2(ft;r0)为距离弯曲因子对ft依赖较强，一般α(ft)较小，使得KS(ft; rref)与Kr相差较小，但这已经足够引起散焦。

经变标两天线相位中心分别为2(r0+rrefα(ft))/c和2(r0+rrefα(ft)+mΔr0)/c[4]，使两个天线成像处理后相位中心不一致，对应像素间存在由路径差引起的失配造成干涉相位误差。因此要对路径差进行校正，将A2的相位中心相对A1移动2mΔr0/c。

文献[7]在系统参数下对非线性近似造成的配准误差以及干涉相位误差进行了分析，在该参数下对距离差采用二次近似即可满足高精度的距离向配准，则Δr0可近似为

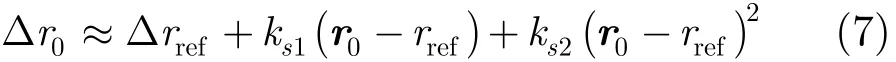
其中ks1，ks2为待定系数，Δrref≈−Bsin(θref−α)为参考位置处路径差，B为基线长度，θref为天线参考位置的视角。经过推导可得系数为(详细推导略)

由文献[7]分析可知，在系统参数给定情况下采用最小二乘拟合两个系数比按式(8)和式(9)计算配准精度更高，因此系数采用最小二乘算法计算得出。

3 非线性近似ECS自配准成像算法

为了补偿由于天线A2和天线A1路径差造成的SAR图像的相位中心不一致，需要将天线A2的相位中心相对于天线A1移动如式(7)所示的Δr0。可以先通过变标处理将天线A2的相位中心移到2(0=r再在距离向频域将相位中心平移ref2/mΔrc后使得两个天线的相位中心一致完成距离向自配准。

由于引入了距离差的非线性近似，因此ECS算法中的原有各相位因子都发生了变化，下面给出了该改进算法的简要推导。

(1)距离向变标处理 变标相位因子设为[6]

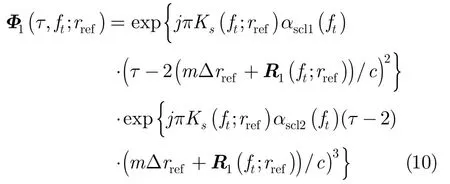
其中αscl1(ft)和αscl2(ft)为待定变标因子。

则将式(5)与式(10)相乘可得

其中Φ是与变标因子有关的3项相位

则式(15)中的第2项可忽略，测绘带W需满足

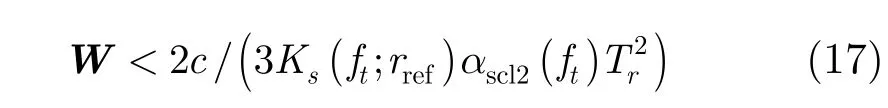
此时式(15)变为

若要使得天线A2变标后的相位中心为′，则要使ψ2≡0，可推导出变标因子

因此变标因子相乘后的信号式(11)变为

其中Δϕ=ψ1如式(13)所示，C1为复常数。

可见通过该变标因子相乘，使得每个距离Chirp相位结构都产生了一个依赖于距离/多普勒的变形，使得所有信号的相位中心都遵从相同的参考弯曲轨迹，相位中心都搬移到的位置。

(2)距离单元徙动校正(RCMC)、距离向聚焦和固定距离移动 对变标后的信号进行距离向FFT变到2维频域，再通过与式(21)相乘来完成距离向聚焦(包括用多普勒依赖变量的2次距离压缩和在调频率中变标的补偿)、距离单元徙动校正和平移：

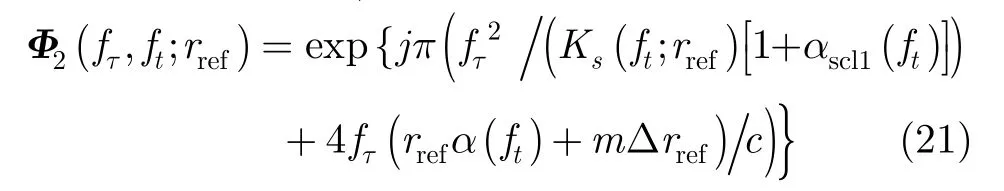
其中fτ为距离向频率，相位项中第1项是距离向聚焦包括2次距离压缩，第2项实现了RCMC和固定的距离向平移。在对式(20)的信号与式(21)的相位函数相乘后，再进行距离向IFFT处理使得包络被聚焦到正确的距离位置2r0/c处，则此时信号变为

(3)残余相位校正 式(22)的第1个相位项是一个正常的多普勒调制，这一项必须在方位向被匹配来对信号聚焦；第2个相位项是原始变标相位相乘产生的残余相位如式(13)所示，需与式(23)的残余相位校正项相乘来消除掉

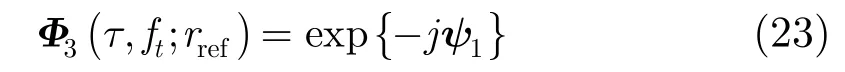
(4)方位向压缩 对残余相位校正后的信号再通过式(24)的相位函数相乘进行方位向压缩处理

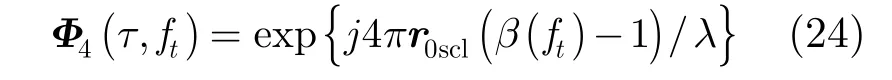
其中r0scl=r0+mΔr0为信号接收时真实路径。

对方位向压缩后信号做方位向IFFT，则可得完全聚焦的SAR图像。此时得到两个天线的SAR图像已具有相同的相位中心，去除了距离向的失配量。

因此可得非线性距离向ECS自配准成像算法的流程如图2所示。与线性ECS自配准算法相比，本文算法在非线性扰动变标、距离压缩、残余相位校正和方位压缩4个部分均做了改进(虚线框部分)，具体的相位表达式文中已给出。可见本文的方法较ECS算法基本没有增加计算量。

图2 非线性距离向ECS自配准成像流程

4 仿真与实测数据验证

(1)变标仿真分析 为对非线性近似变标进行验证[6]，模拟了机载双天线接收1维距离向3个目标chirp信号的非线性变标仿真，仿真参数如表1所示。

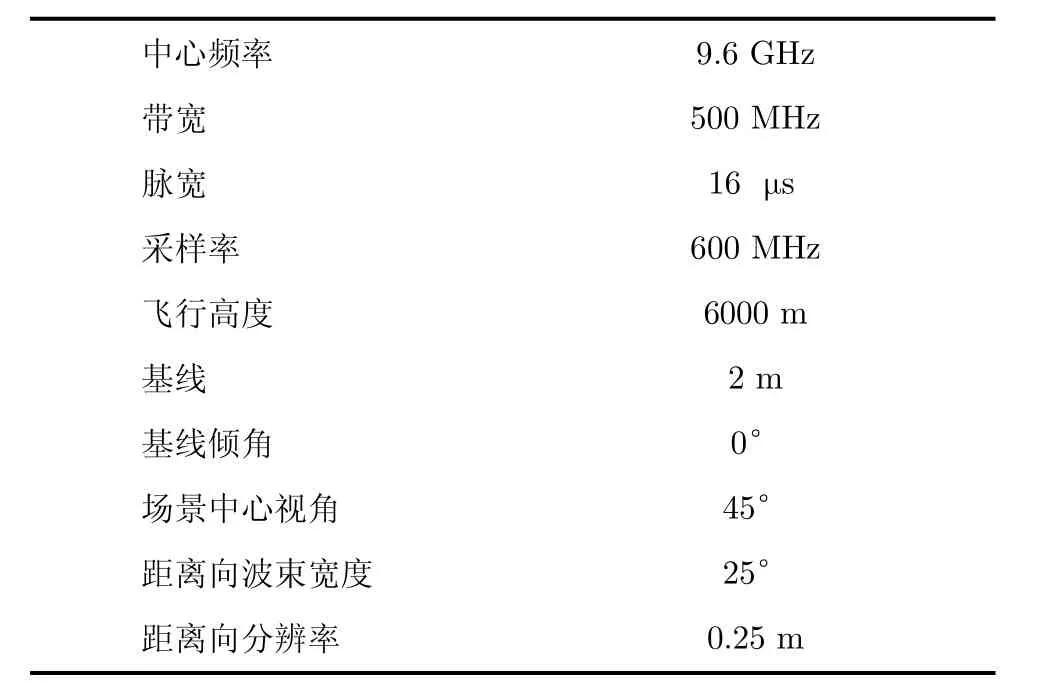
表1 仿真参数

图3给出了两个天线接收回波压缩后中间的点目标结果，图4给出了系统配准误差曲线。

针对图3和图4的仿真结果，表2给出了各个详细参数对应的数据。

由表2的数据可知经过线性变标后，天线A2在距离向基本实现了自配准，但配准精度不够；而非线性变标处理后，天线A2在距离向相对于天线A1完成高精度的配准。3个目标在线性变标后的残余误差理论值分别为：0.164，0.160和0.148个像素；而在非线性变标后残余误差理论值为：0.003，0.008和0.017个像素。通过这些数据比较可知，非线性变标后的残余配准误差比线性变标后明显减小，验证了该算法在距离向自配准方面的有效性。

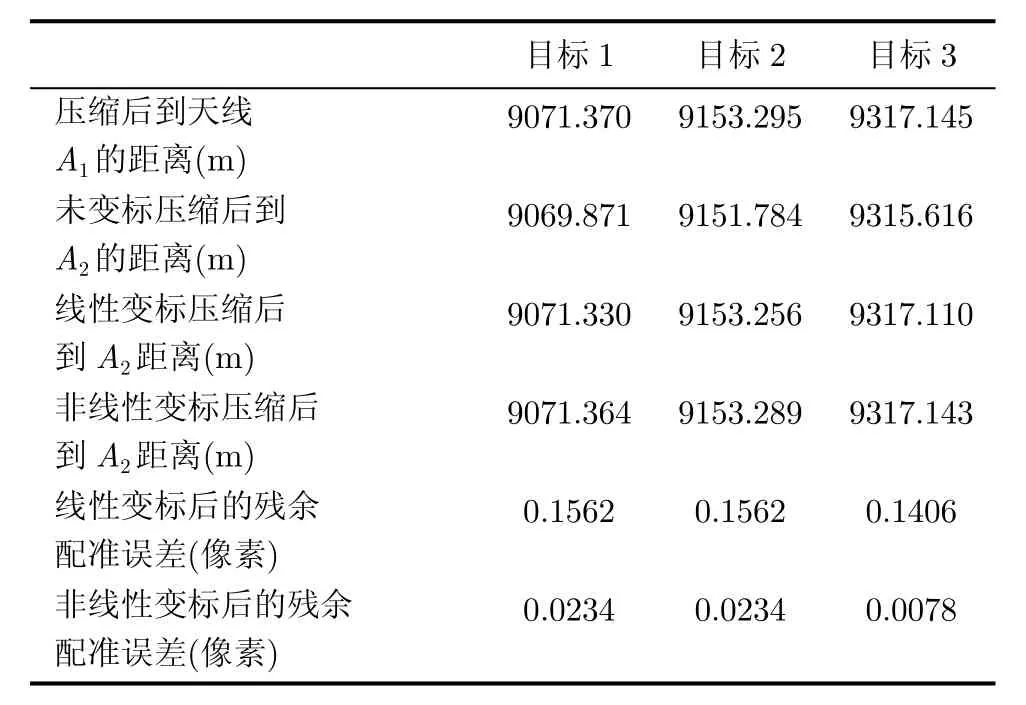
表2 仿真结果各个参数数据

(2)场景的非线性近似距离向自配准仿真 为了更好分析该算法在干涉中的配准效果，对表3参数场景获得两个天线数据进行自配准成像处理，并计算干涉相位和相干系数对自配准结果进行分析。

场景设置是一个半径为200个样本点的锥体，锥体顶部高度50 m。为更好分析配准的效果，将场景目标放置在配准误差较大的测绘区域左部边缘。

图5及图6给出了场景及天线接收的回波，图7和图8分别给出了线性和非线性配准后失配量随距离变化的理论值，每个图均给出了未配准失配量(理论误差)、配准失配量(校正误差)和配准后残余失配量(剩余误差)，其中场景失配量处于图中竖线左侧。对两天线各自接收回波数据进行成像处理并计算干涉相位和相干系数，结果如图9-图14所示。

表3 场景仿真系统参数

图3 两天线接收回波压缩后的结果

图4 配准误差随着距离的变化

图5 场景设置

图6 天线接收回波

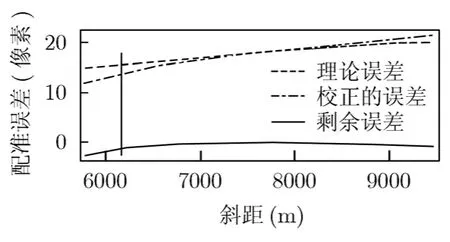
图7 线性配准后失配量变化曲线

图8 非线性配准后失配量变化曲线

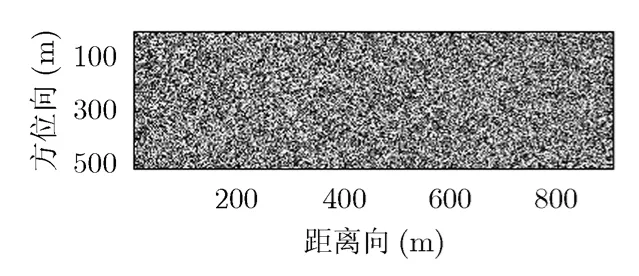
图9 未配准的干涉相位

图10 未配准的相干系数图

图11 线性自配准后的干涉相位

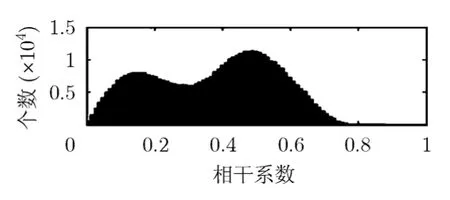
图12 线性自配准后的相干系数

图13 非线性自配准后干涉相位

图14 非线性自配准后的相干系数

表4给出了对3种情况下仿真结果的统计信息(其中γ为相干系数)。

由上面仿真及统计结果可知，由于基线为10 m造成两天线失配量很大，使未配准时看不到干涉条纹，相干系数很低。线性配准后失配量大大减小，但失配量较大区域仍看不到干涉条纹；相干系数有很大提高，但仍有不小噪声。而非线性配准后失配量比线性配准后减小很多，能看到清晰的干涉条纹；相干系数有了显著提高，干涉相位噪声大大较低。

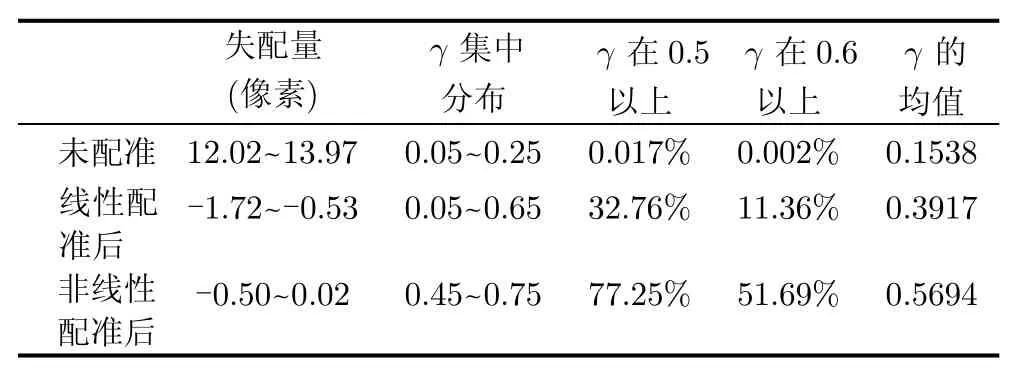
表4 失配量及相干系数统计

(3)实测数据验证 为了对该算法更好验证，下面利用中国科学院电子学研究所的X波段机载双天线干涉SAR数据进行处理分析。图15和图16分别给出了实际数据线性和非线性配准后的配准误差。

图17给出了进行实际数据处理分析的场景幅度图像，图18，图20和图22分别给出了该段数据在3种情况下的干涉相位图，而图19，图21和图23分别给出了相应的相干系数统计图。

图15 线性配准后配准误差变化曲线

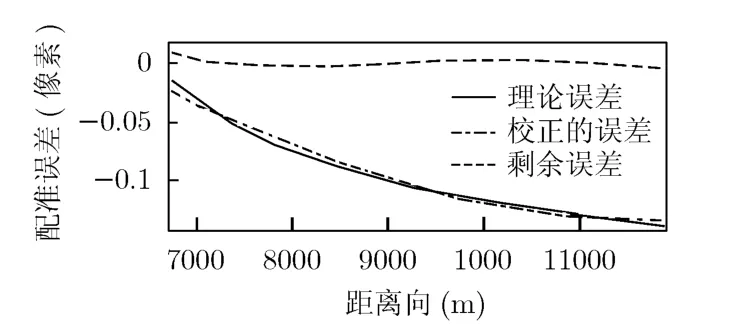
图16 非线性配准后配准误差变化曲线

图17 实际数据对应的场景幅度图

图18 没有配准的场景干涉相位图

图20 线性自配准后场景干涉相位图

图22 非线性自配准后场景的干涉相位图

图19 没有配准的相干系数统计图

图21 线性自配准后相干系数统计图

图23 非线性自配准后相干系数统计图

表5 实际数据的失配量及相干系数统计

由干涉处理结果及表5的统计信息可知，经过非线性自配准处理，相干系数较线性自配准有提高。两种方法效果不很明显是由于系统基线太短(只有0.5568 m)造成系统失配量太小的缘故。

在系统配置为Intel(R)Core (TM) 2 CPU, 6300@ 1.86 GHz 1.86 GHz, 6.00 GB的情况下，对每个天线方位向16384点、距离向4096点的数据进行了处理。传统算法产生高质量干涉条纹需约460 s，而本文提出算法产生高干涉条纹需要约370 s，可见处理速度有了显著提高并且具有较高的配准精度。

5 非线性自配准的精度影响分析

本文提出的非线性近似的自配准算法的配准精度取决于式(7)中两天线路径差的近似精度。一般干涉系统的飞行高度在6000 m左右，天线的下视角在45°左右，因此在表6参数下进行了系统参量对配准精度影响的仿真分析。

表6 各个变量对配准精度影响的仿真参数

仿真结果如图24，图25和图26所示，给出了各参数对应的配准误差的均值和均方根。

由仿真结果可知，随着基线增大，配准误差逐渐增大；当基线长度增加20 m时配准误差平均增大0.03 m，均方误差增加0.14 m。随着基线倾角增大，配准误差有减小趋势；倾角变化70°时配准误差的均值变化了不到0.01 m，均方误差变化约0.02 m。随着测绘带宽增大，配准误差逐渐增大；当测绘带宽由4000 m增至7000 m时，配准误差均值增大了约0.02 m，均方误差增大约0.08 m。

可见基线长度、基线倾角和测绘带宽的大小对非线性配准精度影响很小，它系统参数对配准精度没有影响。对于低于0.3 m 分辨率的系统，配准平均误差没有超过0.1个像素，用非线性近似的自配准算法能较好地配准；对于高于0.3 m 的高分辨率系统，还要考虑成像后的再配准。

6 结束语

本文针对机载双天线干涉系统中出现的距离向失配问题，提出了非线性近似的ECS自配准成像算法。该算法在成像处理阶段完成了距离向失配量的消除，使得系统相干性得到了显著提高，干涉相位的质量较线性自配准有了明显的改善。另外通过系统参数对配准精度的影响分析说明了该算法的实用性。该算法在提高干涉处理速度的同时具有较高配准精度，适合干涉快视处理。但该算法也有不足之处，当地形变化非常剧烈时，配准精度会有较大的降低，为了得到较高的配准精度还需要结合其它配准算法；若地形的坡度变化不大则可以作为恒定坡度进行配准，也能保持较高的配准精度。

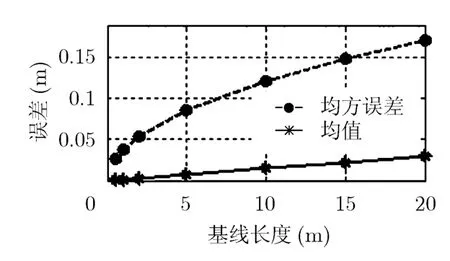
图24 基线长度对精度影响

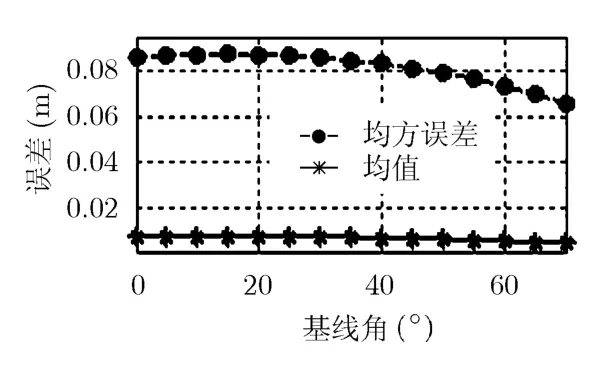
图25 基线倾角对精度影响

图26 测绘带宽对精度影响

参 考 文 献

[1] 吕金建, 文贡坚, 李德仁, 王继阳. 一种新的基于空间关系的特征匹配方法[J]. 测绘学报, 2008, 37(3): 367-373.Lü Jin-jian, Wen Gong-jian, Li De-ren, and Wang Ji-yang. A new method based on spatial relations for feature matching[J].Acta Geodaetica et Cartographica Sinica, 2008, 37(3):367-373.

[2] 王建文, 李青. 基于点和边缘相结合特征提取的图像配准算法[J]. 计算机工程与设计, 2009, 30(4): 928-930.Wang Jian-wen and Li Qing. Image registration algorithm based on extraction of feature point and edge [J]. Computer Engineering and Design, 2009, 30(4): 928-930.

[3] 刘广, 郭华东, 范景辉. 基于外部DEM的InSAR图像配准方法研究[J]. 遥感技术与应用, 2008, 23(1): 72-76.Liu Guang, Guo Hua-dong, and Fan Jing-hui. DEM based SAR image registration method [J]. Remote Sensing Technology and Application, 2008, 23(1): 72-76.

[4] Moreira A, Mittermayer J, and Scheiber R. Extended chirp scaling algorithm for air- and spaceborne SAR data processing in stripmap and scanSAR imaging modes [J].IEEE Transactions on Geoscience and Remote Sensing, 1996,34(5): 1123-1135.

[5] 韦立登, 李绍恩, 向茂生, 吴一戎. 一种新的双天线干涉SAR自配准成像算法[J]. 电子与信息学报, 2004, 26(增刊):237-243.Wei Li-deng, Li Shao-en, Xiang Mao-sheng, and Wu Yi-rong.A novel imaging algorithm with automatic registration for dual-antenna InSAR [J]. Journal of Electronics & Information Technology, 2004, 26(Suppl.): 237-243.

[6] Cumming I G, Wong F H著. 洪文，胡东辉等译. 合成孔径雷达成像—算法与实现[M]. 第1版, 北京: 电子工业出版社,2007: 118-122 and 194-210.

[7] Chen Li-fu, Xiang Mao-sheng, Wei Li-deng, and Han Song-tao. An Airborne interferometric qucik-look processing algorithm. IET International Radar Conference 2009 [C],Guilin China, April 20-22, 2009: 669-673.

[8] Qiu Xiao-lan, Hu Dong-hui, and Ding Chi-biao. Non-linear chirp scaling algorithm for one-stationary bistatic SAR [C].1st Asian and Pacific Conference, Huangshan China, Nov.5-9, 2007: 111-114.