一种改进的CPHD多目标跟踪算法

欧阳成 姬红兵 张俊根

(西安电子科技大学电子工程学院 西安 710071)

1 引言

多目标环境下，由于目标出现、消失及新目标衍生过程的存在，每一时刻的目标数都可能发生变化。此外，观测信息的不确定性，如漏检、虚警等问题均给目标跟踪带来很大困难。如何实时、有效地跟踪数目不定的多个目标，一直是学术界和工程应用的研究热点和难点。

近几年，越来越多专家开始尝试利用随机有限集[1](RFS)理论来解决多目标跟踪问题，其中最有影响力的是Mahler提出的概率假设密度(PHD)滤波[2]。该滤波算法将复杂的多目标状态空间的运算转换为单目标状态空间内的运算，有效避免了多目标跟踪中复杂的数据关联问题。由于PHD递归过程的封闭解无法直接得到，通常采用粒子PHD(particle PHD)[3]或高斯混合PHD(GMPHD)[4]两种方式实现递归。

PHD存在的一个缺点是，假设目标数服从Poisson分布，这会夸大目标漏检对其势估计的影响，这一问题，在最近提出的CPHD滤波算法中得到了改进[5,6]。然而，虽然CPHD对整体目标数的估计是准确的，但从局部看，仍然存在目标漏检问题，即当某个目标发生漏检时，其PHD权值会按照一定的比例转移到其它目标上，这一现象在零虚警概率的情况下显得尤为明显[7]。针对这一问题，文献[7]提出了一种局部化的CPHD算法，该算法将视场按照不同目标划分成多个独立的区域，在每个区域中分别采用CPHD算法进行滤波。该方法需要对划分后各个区域的杂波密度进行调整，这一过程会增加势估计的不确定性，而且当目标发生交叉时，由于无法将目标划分到不同的独立区域，该方法失效。

针对以上问题，本文提出一种改进的CPHD多目标跟踪算法，该算法在高斯混合框架下实现贝叶斯递归，通过对各个高斯分量进行标记，对目标进行航迹关联[8]，在此基础上对修剪合并后各个高斯分量的权值进行再分配。实验结果表明，所提方法不仅能够有效解决目标漏检问题，而且当目标发生交叉时也不会造成目标丢失等情况，在多目标状态估计和航迹维持方面均优于普通的CPHD算法。

2 CPHD滤波

与PHD滤波类似，CPHD也可以采用高斯混合的形式(GMCPHD)实现递归[9,10]。

预测：GMCPHD的预测过程可以分为对PHD的预测以及对势分布的预测两个平行的过程。其中对PHD的预测过程与传统的GMPHD完全相同，这里不再赘述，具体可参考文献[4]。对势分布的预测方程如下：

其中M是一个马尔可夫转移矩阵，它可以通过式(2)计算。

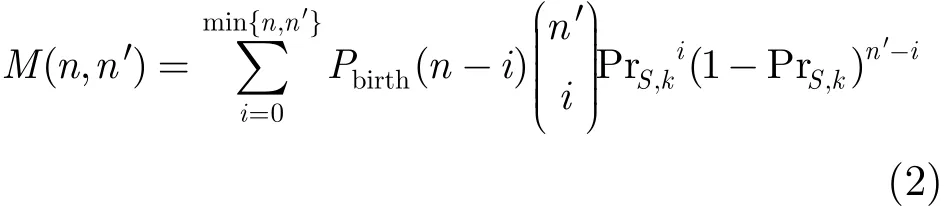
其中PrS,k表示目标的存活概率，Pbirth(n−i)表示k−1时刻到k时刻新生n−i个目标的概率。在恒定采样速率的情况下，M是恒定的，可以预先计算并存储起来。

更新：对PHD和势分布的更新过程可以分别表示为

其中D和¬D分别表示目标被检测到和目标漏检的情况，Pd表示检测概率，各个似然比分别表示如下：

其中λ表示杂波密度，pc(mk−j)表示杂波数为mk−j的概率。

在GMCPHD中，PHD由一些带权值的高斯分量混合表示，其中各个高斯分量的均值和方差可以通过KF迭代求解，高斯分量的权值可按进行更新。设则

基于上述高斯混合模型，式(5)-式(9)中的似然比可以写成Jk|k−1个单检测似然比加权求和的形式：

3 目标漏检问题

第2节介绍的CPHD滤波算法存在固有的目标漏检问题，该问题在零虚警概率的情况下显得尤为明显[7]，因为在上述情况下，式(5)，式(6)，式(8)，式(9)退化成式(15)-式(18)：

考虑只有n个目标的情况，即P(n′＞n)=0，当有一个目标漏检时，有如下式子：

将式(19)，式(20)代入式(15)，式(17)，得到CPHD对于漏检部分PHD的更新方程如下：

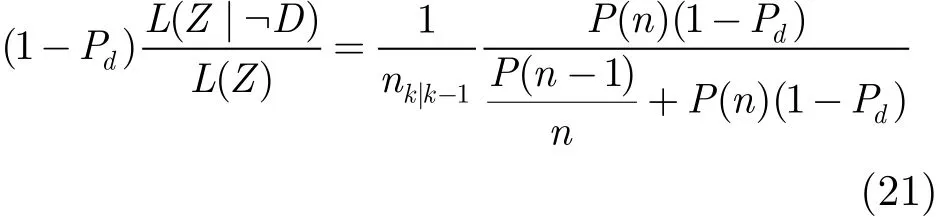
由于这部分PHD是均匀分布在视场中的，而检测部分的PHD只分布在各个观测周围，这就会导致当一个目标漏检时，其PHD权值按照一定的比例转移到其它目标上。这就是CPHD中的目标漏检问题，该问题在传统的PHD中同样存在，因为在传统的PHD中，对于漏检部分的PHD更新方程仅用1−Pd代替式(21)，这与最优贝叶斯估计相距更远，而且它对于整体目标数的估计也是不正确的。

可见，虽然CPHD滤波在单目标零虚警概率的情况下能够准确估计其势分布，但是当把多个目标看作一个随机集进行滤波时，由于CPHD不区分目标，本该在真实漏检目标附近分布的PHD被均匀分散到了整个视场内，致使真实漏检目标的权值变得更小，而检测到的目标由于合并了一部分在视场中均匀分布的PHD，其自身权值反而有所增加。但从全局来看，这种权值的转移不会对势分布的估计造成影响，CPHD滤波对于整体目标数的估计仍然是准确的。

4 改进算法

针对以上问题，本节提出一种改进的CPHD多目标跟踪算法，该算法首先需要对目标做有效区分，采用label法对目标进行标记[8]。设k−1时刻各个高斯分量标记为

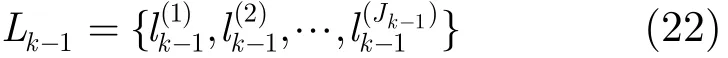
k时刻，预测高斯分量标记为

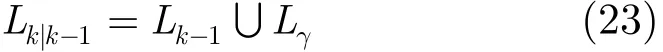
在对PHD的更新步骤中，每个预测高斯分量都会更新出1+mk个高斯分量，将更新后的标记与预测标记对应起来，可得

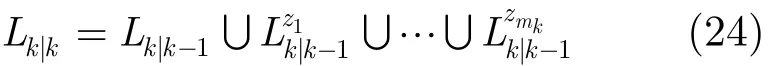
经过修剪合并后，各个高斯分量的标记集合变为

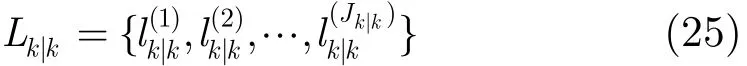
由于更新高斯分量的标记全部来自预测高斯分量的标记集合，所以对于使得成立。

在对目标进行航迹关联的基础上，可以对修剪合并后的高斯分量进行权值再分配，该步骤包含两次分配过程。设k时刻经过修剪合并后的Jk|k个高斯分量中有r个被检测到，Jk|k−r个漏检，由于检测目标的漏检部分PHD一部分源于自身，另一部分由其它漏检目标按照预测权值的比例转移而来，而漏检目标的漏检部分PHD全部源于自身，因此根据式(13)有

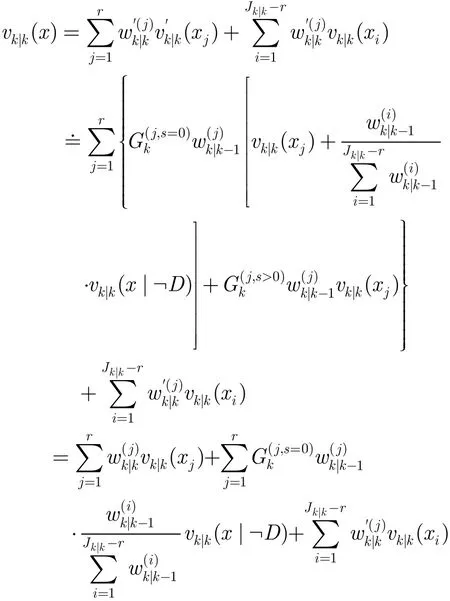
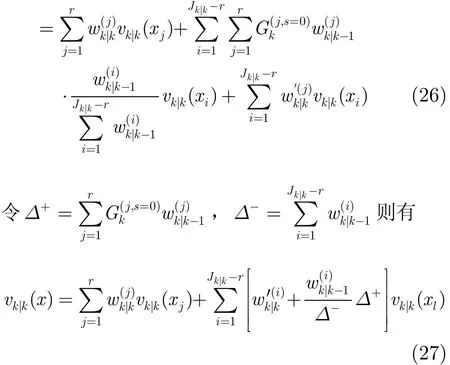
因此在进行第一次分配时，可预先设定一个检测门限η，然后按照式(28)，式(29)进行分配：

由式(28)，式(29)可以看出，第1次分配是以η为标准，认为权值大于η的目标被检测到了，将与其相关的漏检部分PHD按照预测权值的大小分配给权值小于η的高斯分量。其中，检测门限η的选取可根据实际情况进行调整，一般在弱杂波环境将η取大一些，在强杂波环境将η取小一些。

对式(29)中的两部分权值分别求和，可得

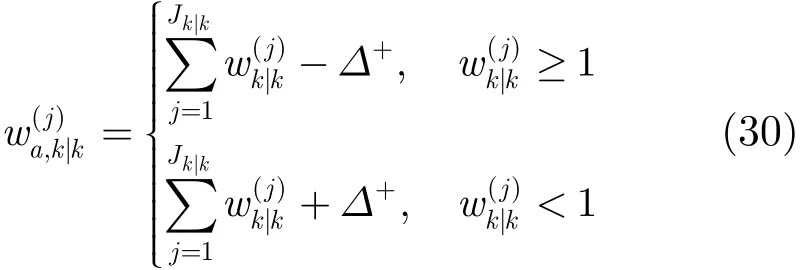
当目标距离很近或发生交叉时，只进行一次权值分配，仍然可能有目标权值大于1，因为多余的权值不仅来自漏检目标，还可能来自与其邻近的目标或杂波。与第一次分配类似，第二次分配可按照下面两个式子进行：

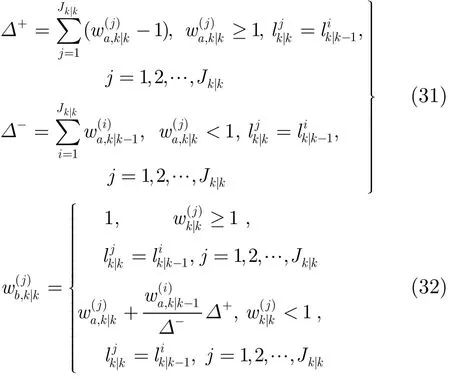
由式(31)，式(32)可以看出，分配过程基于一个目标只可能产生一个观测的事实，将权值大于1的目标直接赋予权值1，而将多余的权值按照预测权值的比例分配给其他目标。与第1次权值分配类似，第2次权值分配仍然不会影响整体目标数的估计，事实上，经过第1次权值分配就能有效解决目标漏检问题，第2次权值分配只在目标距离很近或发生交叉时进行。

5 仿真实验与分析

实验1 研究2维空间中一定区域内的4个目标相继出现消失时的算法性能，每个目标在平面上的运动方程如下：

简单起见，假设目标位置可观测，观测方程为

实验中取σw=0.5，σv=0.5，存活概率PrS,k=0.99，检测概率Pd=0.95。不考虑目标衍生的情况，新生目标随机集服从Poisson分布，其PHD为

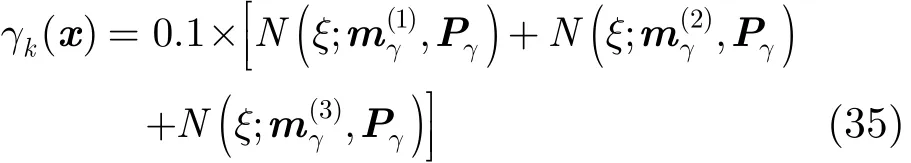
图1所示为CPHD算法分别对4个目标对应高斯分量的权值估计。可以看出，在第13、15时刻，由于目标2漏检，造成了目标1权值的增加，而目标3和目标4由于预测权值比较小，并没有太大变化。同理，在第23、27以及目标消失等时刻均有类似的情况发生。这是由于CPHD并不区分目标，当漏检发生时，漏检部分PHD被均匀分散到了整个视场内，该部分权值按照预测权值的大小进行分配，导致了上述情况发生。图2所示为CPHD算法的目标状态估计，图2(a)为目标在x轴上的位置估计，图2(b)为目标在y轴上的位置估计。可以看出，在漏检时刻，由于漏检目标权值被分散，导致其本身权值变得更小以致低于目标消失阈值ξd，从而在状态估计时认为这些目标消失了。

图3所示为改进算法分别对4个目标对应高斯分量的权值估计。可以看出，在目标漏检时刻，由于对权值进行了再分配，漏检目标分散到其它地方的大部分权值被重新分配回来。虽然也有一小部分权值被分配给了杂波，但由于杂波的预测权值很小，这部分权值只占很小的比例，整体目标数估计仍然是准确的。图4所示为改进算法的目标状态估计。可以看出，在漏检时刻，虽然漏检目标的权值有所下降，但下降的幅度明显减少，其权值仍大于目标出现阈值ψb，从而在状态估计时认为该目标依然存在。

值得注意的是，虽然改进算法在目标漏检时刻的性能得到了较大改善，但当目标消失时，其状态估计有一个滞后效果，该滞后与检测概率Pd有关。对比图2与图4也可以看出，在第40、50和第60个时刻，变权修正的结果导致消失目标的权值下降速度变慢了。上述情况是无法避免的，因为目标漏检与目标消失在单帧内无法区分，当检测概率Pd＜1时，在目标消失后的1个到几个时刻内，该目标被当作漏检而认为依然存在是符合客观实际的。

实验2 考察目标发生交叉时算法的性能。令σw=0，其它仿真参数同实验1，产生理想运动轨迹如图5所示，4个目标分别在第26和第51时刻发生交叉。

图6所示为CPHD算法分别对4个目标对应高斯分量的权值估计。可以看出，在第4，第16和第65时刻，由于目标3，目标1和目标4漏检，造成了其余目标权值的增加，另外，在交叉点附近，由于目标交叉而导致了一部分权值转移。

图7所示为只进行一次权值分配的结果。可以看出，通过第1次权值分配，由于目标漏检所导致的权值转移问题得到了解决，但由于目标交叉而导致的权值转移问题依然存在。

图8所示为改进算法的最终分配结果。可以看出，通过两次权值分配，由于目标交叉所导致的权值转移问题也得到了很好的改善。

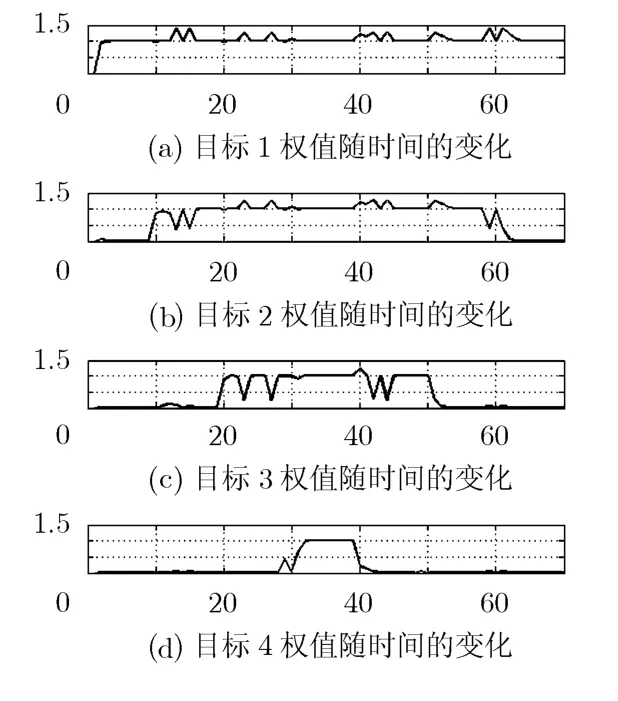
图1 CPHD对4个目标的权值估计

图2 CPHD的目标状态估计

图3 改进算法对4个目标的权值估计

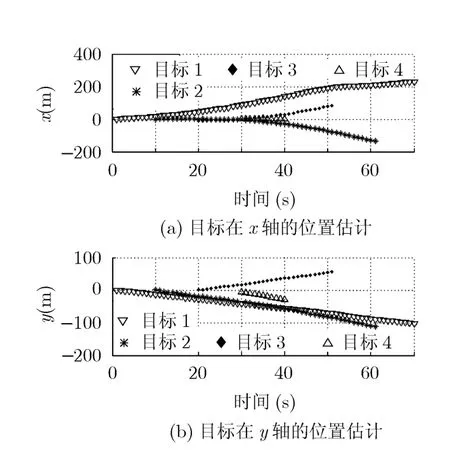
图4 改进算法的目标状态估计

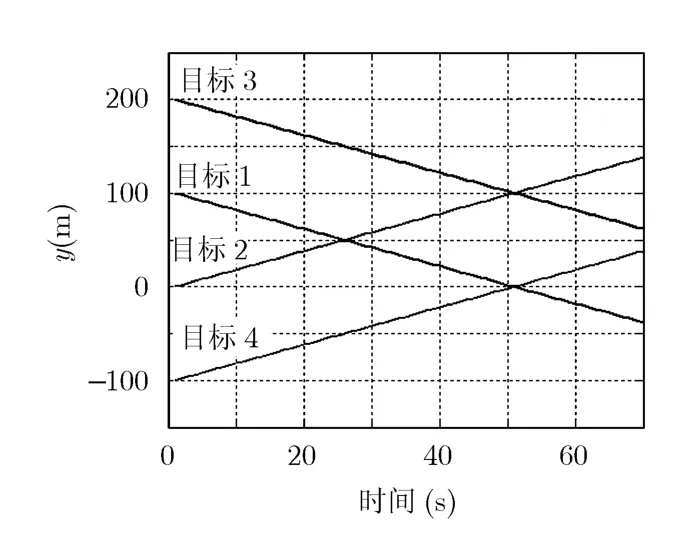
图5 4个目标在y轴上的理想运动轨迹

图6 CPHD对4个目标的权值估计

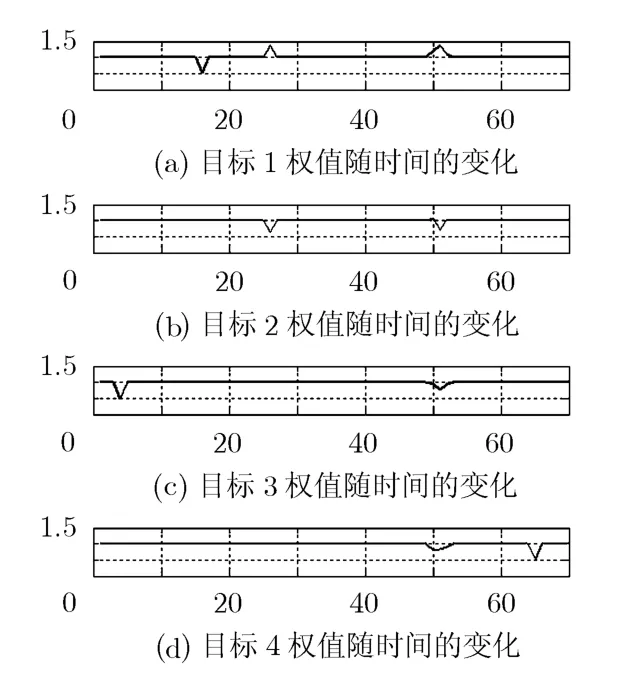
图7 只进行第1次权值分配的结果

图8 改进算法的最终分配结果

6 结论

本文针对CPHD算法中的目标漏检问题，提出一种改进的CPHD多目标跟踪算法。算法首先将数据关联引入CPHD中，在有效区分目标的基础上对修剪合并后各个高斯分量的权值进行再分配。首先通过第1次分配解决目标漏检所导致的权值转移问题，若目标发生交叉，则对权值进行第2次分配。实验结果表明，所提方法不仅能够有效解决目标漏检问题，而且在目标发生交叉时也不会造成目标丢失等情况，在多目标状态估计和航迹维持方面均优于普通的CPHD算法。CPHD算法的复杂度较高，如何对参数进行优化，进一步提高算法效率都是今后需要开展的工作。

[1] Goodman I, Mahler R, and Nguyen H. Mathematics of Data Fusion [M]. Norwell, MA, Kluwer, 1997: 131-175.

[2] Mahler R. Multitarget Bayes filtering via first-order multitarget moments [J]. IEEE Transactions on Aerospace and Electronic Systems, 2003, 39(4): 1152-1178.

[3] Vo B N, Singh S, and Doucet A. Sequential Monte Carlo methods for Bayesian multi-target filtering with random finite sets [J]. IEEE Transactions on Aerospace and Electronic Systems, 2005, 41(4): 1224-1245.

[4] Clark D, Vo B T, Vo B N, and Godsill S. Gaussian mixture implementations of probability hypothesis density filters for non-linear dynamical models [C]. IET Seminar on Target Tracking and Data Fusion: Algorithms and Applications,Birmingham, UK, April 15-16, 2008: 21-28.

[5] Mahler R and Martin L. PHD filter of high order in target number [J]. IEEE Transactions on Aerospace and Electronic Systems, 2007, 43(4): 1523-1543.

[6] Mahler R. PHD filter for nonstandard targets, Ⅱ:Unresolved targets [C]. 12th International Conference on Information Fusion, Las Vegas, NV, USA, July 6-9, 2009:922-929.

[7] Ulmke M, Franken D, and Schmidt M. Missed detection problems in the cardinalized probability hypothesis density filter [C]. 11th International Conference on Information Fusion, Cologne, Germany, June 30-July 3, 2008: 1-7.

[8] Erdinc O, Willett P, and Coraluppi S. The Gaussian mixture cardinalized PHD tracker on MSTWG and SEABAR’07 datasets[C]. 11th International Conference on Information Fusion, Cologne, Germany, June 30-July 3, 2008: 1-8.

[9] Vo B T, Vo B N, and Cantoni A. Analytic implementations of the cardinalized probability hypothesis density filter [J].IEEE Transactions on Signal Processing, 2007, 55(7):3553-3567.

[10] Ulmke M, Erdinc O, and Willett P. Gaussian mixture cardinalized PHD filter for ground moving target tracking[C]. 10th International Conference on Information Fusion,Quebec, Que, July 9-12, 2007: 1-8.