数字通信系统中的Monte Carlo仿真

高明慧

（华中师范大学电子信息工程，湖北武汉430079）

1.序言

随着数字通信技术的发展及对通信质量的的要求越来越高，数字通信获得飞速发展，成为当代通信技术的主流。与模拟通信系统相比，数字通信系统有很多优势：传输差错可控、抗干扰能力强、易再生中继且无噪声积累等。而在数字通信系统中，从接收端的角度看，发送哪一个可能的信号波形是不确定的；且信号在信道传输过程中又会受到加性高斯白噪声的干扰，因此这种发送信号的不确定性与噪声的随机性，导致接收波形是一个随机波形，故在接收端作判决时会不可避免地出现错判，也即存在一定的差错概率。因此常常需要利用某种方法对一个数字通信系统进行差错概率评估，以评价该数字通信系统的可靠性，以及根据评估的结果进一步改善系统性能以使得系统的错判概率达到最小。

2.Monte Car lo算法简介

蒙特卡罗(Monte Carlo)方法，也称计算机随机模拟方法，是一种基于"随机数"的计算方法。它源于美国在第二次世界大战研制原子弹的"曼哈顿计划"。该计划的主持人之一用驰名世界的赌城-摩纳哥的Monte Carlo-来命名这种方法，为它蒙上了一层神秘色彩。20世纪40年代中期，由于科学技术的发展和电子计算机的发明，Monte Carlo方法作为一种独立的方法被提出来，并在核武器研究中首先得到应用，但其基本思想很早就已经被人们发现与利用，例如：计算平面上的一个单位边长的正方形及其内部的一个形状不规则的"图形"的面积时，Monte Carlo方法"随机化"的思想就是向该正方形"随机地"投掷N个点，若有M个点落于"图形"内部，则该"图形"的面积近似为M/N。蒙特卡罗方法广泛应用在金融工程学、宏观经济学、计算物理学等领域中，在现代通信系统中蒙特卡罗（Monte Carlo）计算机仿真主要用于估算数字通信系统的误码率，特别适用于难以对判决器的性能进行分析的情况。

3.数字通信系统中Monte Carlo仿真的一般条件

为了计算出样本值N应该满足什么条件时利用Monte Carlo估计差错概率能较逼近理论值，我们现在考虑利用Monte Carlo仿真估计一个随机变量Y=m+G，Y＜0的概率情况，即P(m)=P(Y＜0/m)，其中m为某个给定的正值，G为零均值、方差为1的高斯随机变量，则Y就是一个均值为m，方差为1的高斯随机变量。

我们利用一个统计独立的、同分布的、0均值的单位方差高斯随机变量Gi，i=1，2，…，N，加上正值m来得到随机变量序列：Yi=m+Gi，i=1，2，…，N。分析随机变量的概率密度，我们定义估计值为概率密度函数的面积，即有P'(m)=，当Yi＜0时Xi=1，也就是Yi＜0(i=1，2，…，N)个数与总随机变量N的比值，这种估计思想与Monte Carlo基本算法一致。

为了使验证估计值能较好地逼近真正概率，我们计算估计的均值和方差。有

由此说明估计P'(m)的均值等于真正的P(m)的均值，即是无偏估计。

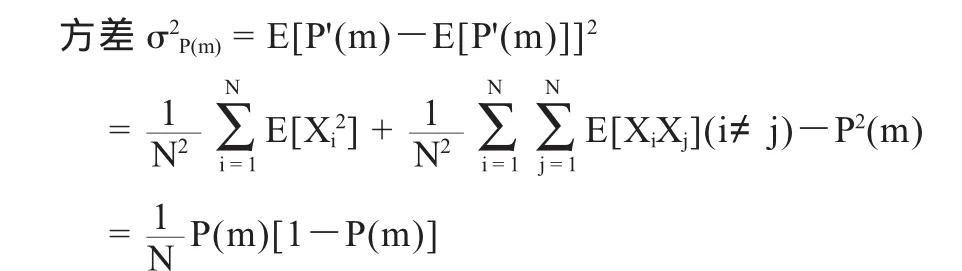
如果假设对较小概率（即P(m)＜＜1）进行估计，为了保证估计的标准偏差比P(m)更小，我们假定则有，又由于P(m)＜＜1，因此有，所以在加性噪声和加性干扰存在的情况下，对数字通信系统的差错概率进行估计时，一般应该满足这个条件，但通常当P(m)＜＜1时，满足就足够了。下面我们就以二进制数字通信系统为例对数字通信系统的Monte Carlo仿真进行详细分析。

4.二进制数字通信系统的Monte Carlo仿真

4.1 二进制通信系统理论差错概率分析

在二进制数字通信系统中，我们常用波形信号S0(t)和S1(t)来表示0和1组成的二进制数据，假设数字速率为R(bps)，且传输信号的信道为加性高斯白噪声（AWGN）信道，则序列0和1与信号波形S0(t)和S1(t)的映射关系可以表示为：

0→S0(t)，0≤t≤Tb

1→S1(t)，0≤t≤Tb(其中Tb＝定义为比特时间区间)

接收到的信号r(t)则表示为：r(t)=Si(t)+n(t)，i=0，1，其中n(t)是功率谱为常数N0的加性高斯白噪声，这样在接收2端我们将利用信号相关器（或匹配滤波器）与检测器对接收到的信号r(t)进行判断，确定发送端在0≤t≤Tb时刻发送的是0还是1。

因为信号相关器的原理是将接收到的信号r(t)与两个发送端信号S0(t)和S1(t)进行互相关运算，在t=Tb时对这两个输出进行采样（容易证明匹配滤波器在t=Tb时刻的输出与信号相关器的输出是一样的），并将采样输出反馈给检测器，信号相关器原理图如图1所示。假设两个信号波形S0(t)和S1(t)是正交的，即后面的计算中有且发送的信号为S0(t)，则接收到的信号就为r(t)=S0(t)+n(t)，0≤t≤Tb。

计算得信号相关器的输出为：

由此得，r0和r1的概率密度函数分别表示为：

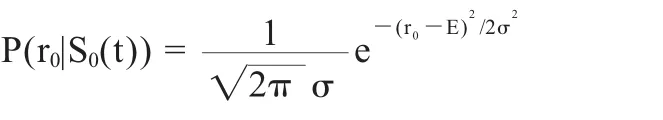
因此发送S0(t)信号波形的差错概率为：

同理我们也可以计算出发送S1(t)信号的差错概率和发送S0(t)同。

下面我们来计算随机变量x=(n1－n0)的方差：

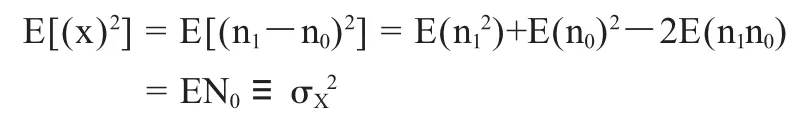
4.2 利用Monte Carlo仿真差错概率分析

实际中我们常常以用Monte Carlo计算机仿真来估计数字通信系统的差错概率，特别是对检测器的性能难以分析时。二进制数字通信系统中Monte Carlo仿真的模型如图3所示：

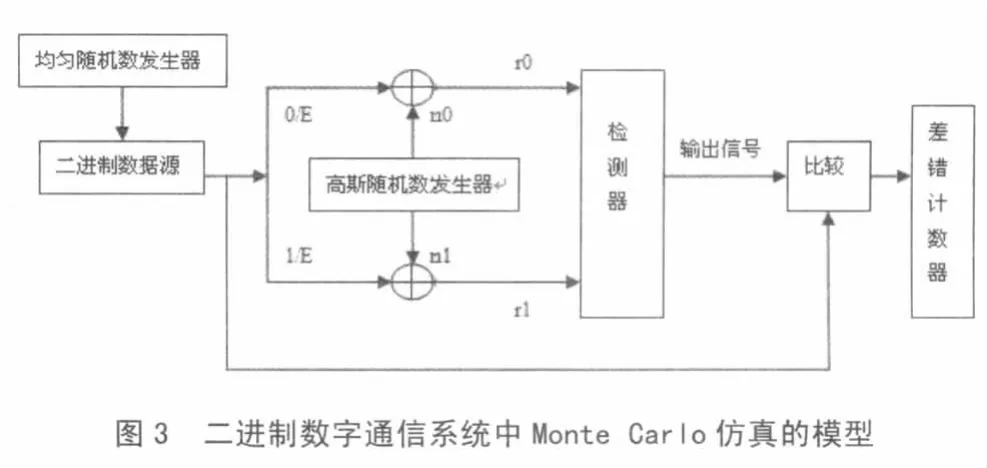
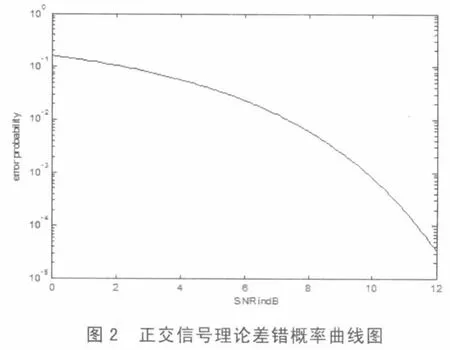
在图3的仿真模型中我们先由一个产生范围在（0，1）内的均匀随机发生器决定等概率出现并且互为统计独立的二进制0和1的序列。当产生的随机数在（0，0.5）内时，二进制源输出0，否则输出1；因此当产生0时，信号相关器输出r0＝E+n0，r1＝n1；当产生1时，r0＝n0，r1＝E+n1。最后由差错计数器统计出比特差错数，并得出差错数与采样值N的比值。为满足我们前面分析的利用估计概率时应满足的条件，我们取在不同SNR值下，采样N=10000。同时为了与理论值进行比较，我们也将理论值在图中同时绘出，仿真结果如图4所示。

从图4我们可以看出估计概率值与理论概率值基本一致，应用类似的算法也可以得出在其它形式的数字通信系统中，Monte Carlo仿真估计差错概率与相应的理论概率具有一致性，这也就是Monte Carlo在数字通信系统中可以仿真差错率的准确性与可靠性，因此在数字通信系统中我们常常利用Monte Carlo仿真估计系统的差错概率。

5.结束语

蒙特卡罗(Monte Carlo)方法是一种基于"随机数"的计算方法，其在很多领域都得到广泛应用。在数字通信系统中，常常利用Monte Carlo仿真对存在噪声和干扰的通信系统进行差错概率估计。通过二进制数字系统理论与仿真的差错分析，我们从中得出Monte Carlo对数字通信系统差错概率仿真的准确性与重要性。

[1] 刘树棠译.现代通信系统（MATLAB版）[M].北京：电子工业出版社，2008.

[2] 王立宁，乐光新等.MATLAB与通信仿真[M].北京：人民邮电出版社，2000.

[3] 唐向宏，岳恒立等.MATLAB及在电子信息类课程中的应用[M].北京：电子工业出版社，2006.