在三轴插齿机上实现非圆齿轮磨齿运动的方法
2010-03-24李建刚李泽湘
李建刚,周 磊,赵 巍,李泽湘,2
(1.哈尔滨工业大学深圳研究生院,518055深圳,hit.li.jg@gmail.com;2.香港科技大学电子及计算机工程学系,香港)
非圆齿轮因其能够按照一定的变传动比运动,在工业上应用得越来越多,其加工精度的要求也越来越高.非圆齿轮的磨齿问题是一个未能解决的突出难点,严重影响了非圆齿轮在重载和高精度方面的应用[1-7].
成形砂轮展成磨削法是一种全新的非圆齿轮磨削方法[1].该方法把成形砂轮看作插齿刀的一个刀齿,利用非圆齿轮插齿加工过程中齿廓成形原理,推导出了非圆齿轮齿廓的成形砂轮展成磨削方法.
本文在上述方法基础上对非圆齿轮和砂轮的空间位置关系进行分析研究.提出了在三轴非圆齿轮插齿机上增加磨头装置来实现非圆齿轮的磨齿,给出了非圆齿轮磨削无Z方向运动进行分度的原理和计算方法,以及由四轴磨削运动到三轴磨削的运动转换方法.
1 非圆齿轮齿廓的成形砂轮展成磨削原理[1]
非圆齿轮插齿加工是将插齿刀看作一个圆齿轮,根据非圆齿轮和圆柱齿轮啮合原理,计算得到在插齿过程中非圆齿轮和插齿刀的相对运动关系,表示为非圆齿轮转角φi及其中心O的XY坐标xi,yi和插齿刀的旋转运动ψi,如图1所示.即可以通过N组四轴点位坐标来控制四轴数控插齿机床来实现插制非圆齿轮,一组点位坐标可以表示为Pi(ψi,φi,xi,yi),其中i=0,1,2,…,N.
这里所说的成形砂轮,就是把盘状砂轮的廓形修成齿数为Z0的渐开线圆柱齿轮的一个牙齿的形状(见图1).它磨削非圆齿轮一个齿槽的过程就相当于齿数Z0的齿轮和非圆齿轮一个齿槽的啮合过程.图2表示瞬时成形砂轮磨削非圆齿轮第3个齿槽时的砂轮和非圆齿轮的位置关系.文献[1]给出了磨削非圆齿轮第k个齿槽时,插齿刀和非圆齿轮相对四轴运动点序列Pi从i= TSk到i=TEk之间,相对应的成形砂轮和非圆齿轮的四轴运动数据(εk,i,φk,i,xk,i,yk,i)可以计算得到,这里不再赘述.
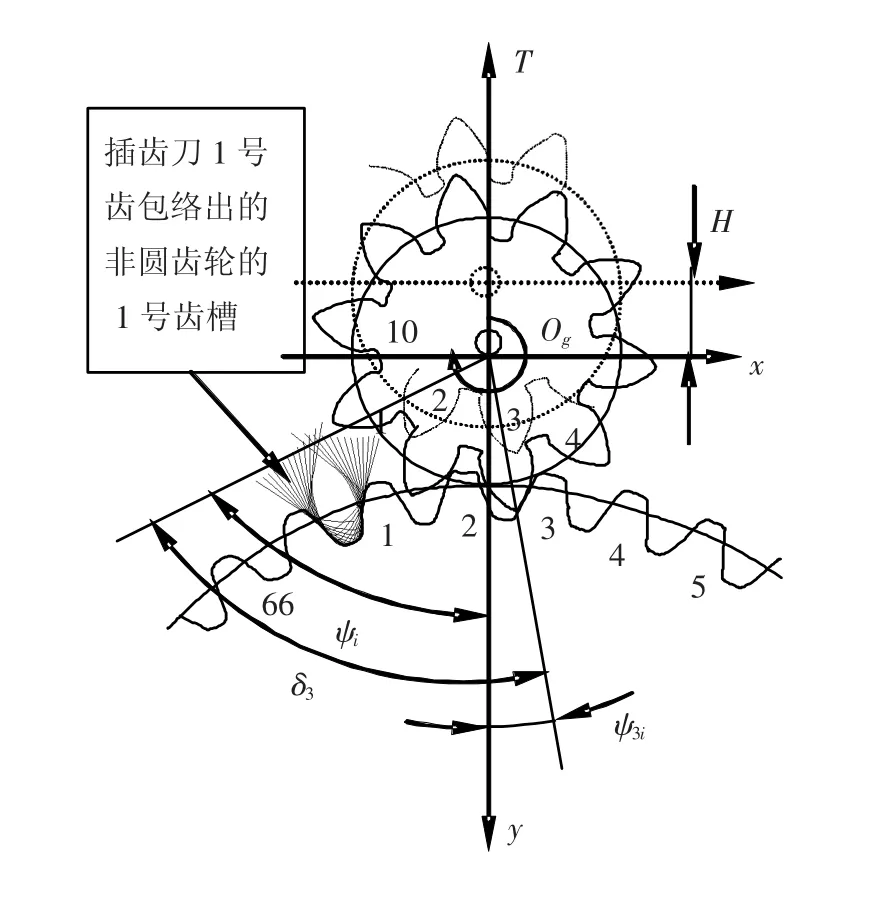
图1 插齿刀刀齿包络非圆齿轮齿槽图[1]
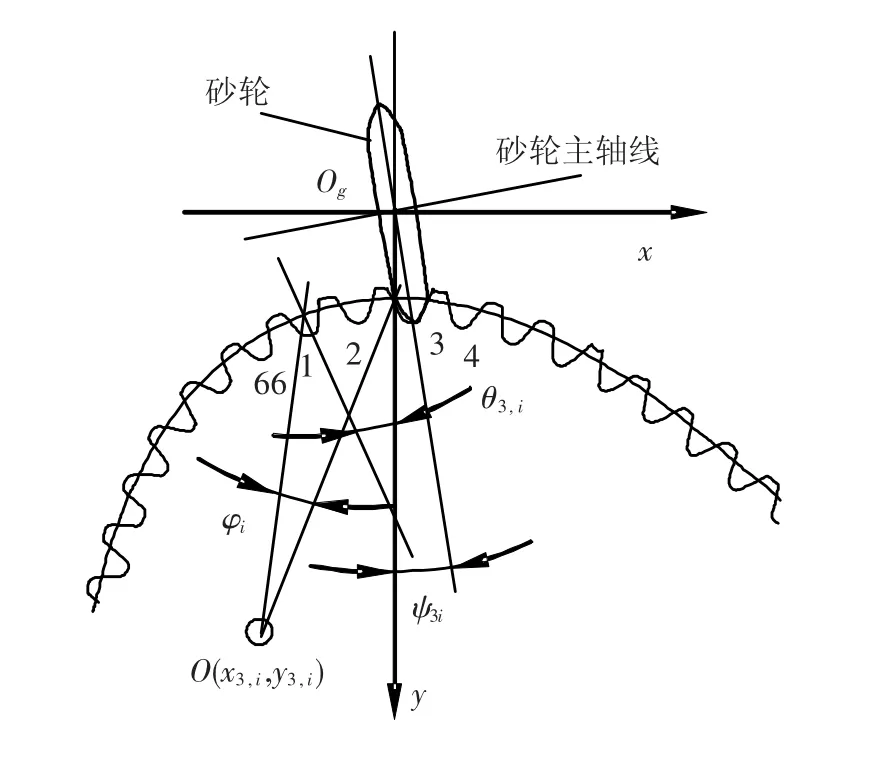
图2 磨削非圆齿轮第3个齿槽时砂轮和非圆齿轮之间的位置关系图[1]
磨削完一个齿槽后,工件和砂轮作分度运动,接着按照齿轮Z0的下一个牙齿与非圆齿轮的下一个齿槽作啮合运动磨削,采用的是一种间隙的展成磨法.
2 非圆齿轮磨削机床的分析
如果要设计一台符合该原理的非圆齿轮磨齿机床,需要上述四轴联动来实现展成磨削运动.同时,需要设计磨头使砂轮沿自身轴线高速旋转,形成磨削速度.为了磨到非圆齿轮全齿宽,磨齿过程中砂轮需要沿z方向上下移动,类似于插齿过程中的插齿刀沿自身轴线z往复切削齿廓的运动.
但是,目前没有满足上述要求的齿轮磨床,如果要单独开发一台样机,不仅周期长,而且非常昂贵.考虑到该磨削原理是从非圆齿轮插齿加工原理演化而来,最直接的验证方法就是在非圆齿轮插齿机床中,将插齿刀替换成高速旋转的砂轮来进行加工实验.下面就着重讨论在插齿机上通过增加磨头来实现磨齿的运动计算问题.
从非圆齿轮成形砂轮展成磨削原理可知,如果假定砂轮中心不动,它们之间的位置关系可以用砂轮的转动,非圆齿轮中心在平面两个方向的移动和绕自身中心的转动这4个运动来实现.根据微分几何原理,两个物体在平面内的相对位置关系最多只有3个自由度,即只需要用前面这4个运动中的3个运动就可以表示出它们在平面内的相对位置关系.同时,在实际工业生产中,已经有一批三轴联动的非圆齿轮插齿机床在实际中应用,其运动(见图3)基本满足非圆磨齿的运动需要,只需在插齿刀刀杆上安装成形砂轮磨头,就能实现非圆齿轮磨齿的需要,如图4所示.下面就给出在三轴插齿机床中实现非圆齿轮磨齿分度和每一个齿的加工展成运动的转化关系.
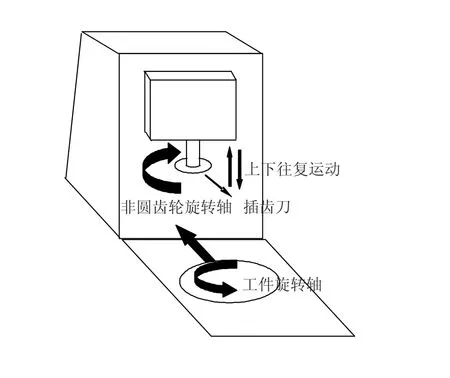
图3 三轴插齿机的运动简图

图4 增加了磨头的三轴插齿机的运动简图
3 无干涉无抬刀磨削分度四轴运动的实现
在分度过程中,如果要保证砂轮和非圆齿轮不发生干涉,最简单的方法就是将砂轮沿齿轮轴向上移到一个安全平面后再进行分度,但是这样就需要增加一个分度Z轴.而大部分非圆齿轮插齿机没有这个运动.这样,在利用数控非圆齿轮插齿机来实现非圆齿轮磨齿时,加工完一个齿后必须给出合适的分度运动来避免砂轮和齿轮的干涉.
为了解决上述问题,根据非圆齿轮啮合原理[3-4],在插齿加工过程中,插齿刀如果沿着图1所示的T方向(插齿刀节圆和非圆齿轮节曲线的切线方向)移动H距离,到图1所示的虚线位置(插齿加工的切入初始位置),则按照原来的插齿数据运动,非圆齿轮和插齿刀不会相接触,其中H可以由下式确定:
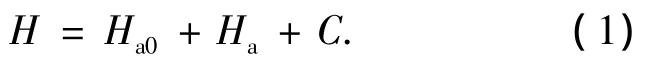
其中:Ha0为插齿刀的齿顶高,Ha为非圆齿轮齿顶高,C为一个大于零的数,其值由齿轮节曲线的最小曲率半径和插齿刀的半径决定.
在磨削过程中,磨削完非圆齿轮第k个齿槽对应的插齿刀和非圆齿轮相对四轴运动点序列Pi为i=TEk,非圆齿轮第k+1个齿槽开始磨削时对应的插齿刀和非圆齿轮相对四轴运动点序列Pi为i=TSk+1.首先,利用文献[1]给出的公式,通过修正插齿刀和非圆齿轮相对四轴运动点序列Pi从i=TEk到i=TSk+1之间的数据Pi(ψi,φi,xi,yi)成为P'i(ψi,φi,xi,yi±H)(正号对应外齿轮,负号对应内齿轮);其次,计算出砂轮和非圆齿轮的相对运动数据(ε'i,k,φ'i,k,x'i,k,y'i,k);最后,让砂轮和非圆齿进行联动来实现分度.砂轮和非圆齿轮在没有干涉的情况下完成了分度.
以上分析表明:非圆齿轮磨齿不需要磨头上移分度,即可在原有磨齿原理计算数据中完成分度.
因此,可以很容易得到磨削非圆齿轮由第k个齿槽包络过程为(εk,i,φk,i,xk,i,yk,i),i=TSk,TSk+1,…,TEk和第k+1个齿槽分度过程(ε'i,k,φ'i,k,x'i,k,y'i,k),i=TEk,TEk+1,…,TSk+1两部分组成.
4 非圆齿轮磨齿在三轴插齿机上的运动等效转化
从相对运动关系来说,为了实现插齿刀节圆和非圆齿轮节曲线任意瞬时相切纯滚动,在不考虑切点位置情况下,插齿刀和非圆齿轮的相对位置关系可以用插齿刀的回转、非圆齿轮的回转以及插齿刀和工件中心距的变化3个参数来实现[8-11].如果在该机床上实现非圆齿轮磨齿,需要将第一节计算的四轴插齿数据(εk,i,φk,i,xk,i,yk,i)和第三节计算的分度数据(ε'i,k,φ'i,k,x'i,k,y'i,k)进行等效运动转化.
因为三轴和四轴相比,缺少X方向的运动,如图5所示,建立新的坐标系,在运动过程中砂轮中心Og和非圆齿轮中心O都在¯y轴上[12].根据平面坐标转化关系,从坐标系Og-x,y到坐标系中,(εk,i,φk,i,xk,i,yk,i)可以转化成为,具体公式为
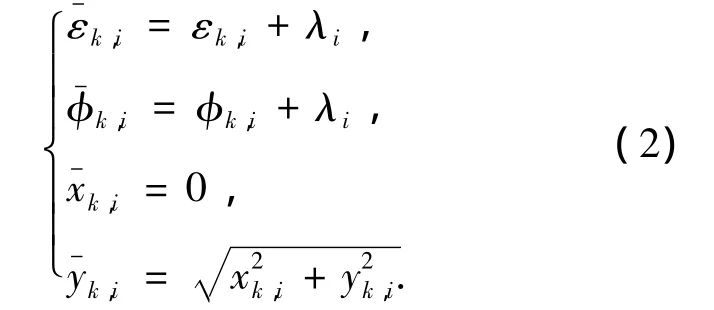
其中:λi=arctan(yk,i/xk,i).
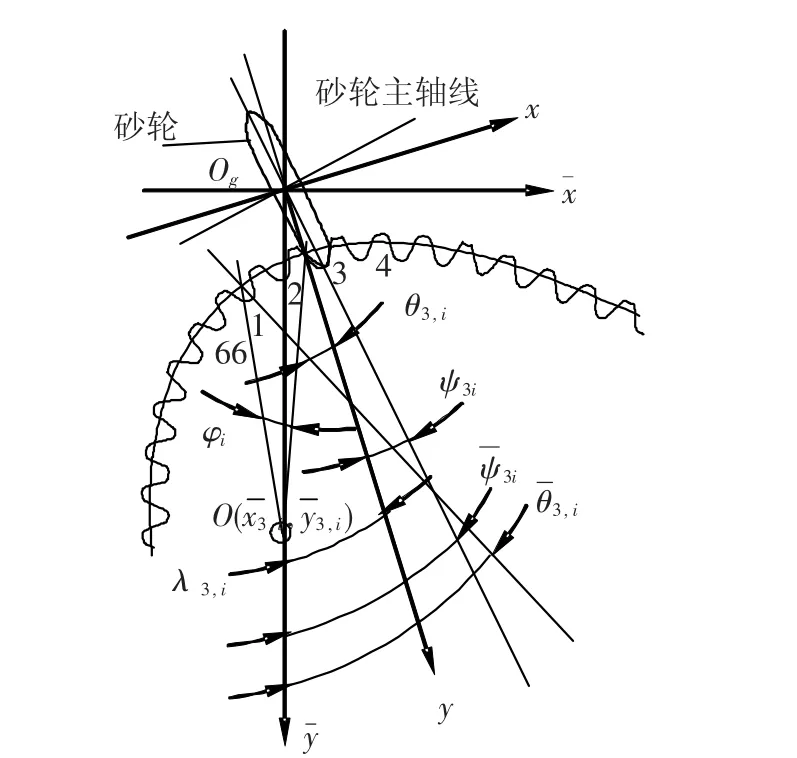
图5 四轴磨齿到三轴磨齿的运动转化图
5 结论
1)提出了在国内已有的非圆齿轮三轴插齿机床上增加磨头的形式来实现非圆齿轮磨齿.
2)考虑到插齿机没有Z轴控制运动的实际情况,解决了在不用抬刀、不产生干涉情况下的磨削分度问题,并给出了由四轴磨削运动到三轴磨削运动的转化公式.
3)对非圆齿轮磨齿加工原理在现实中的应用进行了理论研究,使非圆齿轮磨齿加工成为可能,有利于非圆齿轮在精度要求高的场合中应用.
[1]贺敬良,李建刚.非圆齿轮的成形砂轮展成磨削原理研究[J].农业机械学报,2007,38(10):145-149.
[2]李建刚,吴序堂,李泽湘.基于插齿模型的非圆齿轮根切分析[J].农业机械学报,2007,38(8):138-142.
[3]吴序堂,王贵海.非圆齿轮及非匀速传动[M].北京:机械工业出版社,1997.
[4]吴序堂.齿轮啮合原理[M].北京:机械工业出版社,1983.
[5]李建刚,吴序堂,毛世民,等.非圆齿轮齿廓数值计算的研究[J].西安交通大学学报,2005,39(1):75-78.
[6]HORIUCHI Y.On the gear theory suggested by leibnitsthe analysis of non-circular gears-Bull[J].Journal of the Japan Society for Precision Engineering,1989,23 (2):146-151.
[7]LITVIN F L.Gear geometry and applied theory[M].New York:Prentice-Hall,1994:103-145.
[8]KATORI H,HAYASHI T.Simplified synthetic design method of pitch curves and tooth profiles for noncircular gears[C]//Proceedings of 1989 International Power Transmission Gearing Conference on New Technological Power Transmission 90's.Chicago,Illinois:[s.n.],1989:527-532.
[9]DOONER D B.Use of noncircular gears to reduce torque and speed fluctuations in rotating shafts[J].ASME Journal of Mechanical Design,1997,119(3): 299-306.
[10]CHANG S L,TSAY C B.Mathematical model and undercutting analysis of elliptical gears generated by rack cutters[J].Mechanism and Machine Theory,1996,31 (7):879-890.
[11]SHIH-HIS T,DANIEL C H.Yong.Generation of identical noncircular pitch curves[J].Mechanical Design,1998(2):337-341.
[12]CLEGHORN W L,SHOW E C.Computer analysis of continuously variable transmissions using noncircular gears[J].Transactions of the CSME,1987,11(2):113-120.
