半球谐振子动力学方程的建立及固有频率的计算

赵洪波，任顺清，李 巍

(哈尔滨工业大学空间控制与惯性技术研究中心，哈尔滨150001，h84b@163.com)

半球谐振陀螺仪是一种哥氏振动陀螺仪，已在卫星和宇宙飞船中得到广泛的应用［1－2］，其高精度、长寿命特性使其在空间技术方面有广阔的应用前景，国内从十一·五期间已开展了半球谐振陀螺仪的研制工作.在理论与实际应用中半球谐振子的固有频率是一个很重要的参数，特别是在由于谐振子密度、厚度等的不均匀性造成的半球谐振子频率裂解的分析中有重要的作用.文献［3］通过有限元法计算了半球谐振陀螺仪谐振子的固有频率，文献［4］给出了半球谐振陀螺仪谐振子的固有频率的计算公式，但根据此公式编程计算的值与实测的固有频率相差太大.因此本文经过一系列的推导，建立了与文献［4］不同的动力学方程，给出了固有频率的计算方法，并结合某半球谐振陀螺仪的具体参数给出了计算的固有频率，这个频率与实测结果相近.再取文献［3］的一组半球谐振陀螺仪的基本参数，按照本文的方法进行计算并和文献［3］的结果比较，证明了本文方法的正确性.

1 半球谐振子动力学方程

1.1 半球谐振子任意点的应变方程

如图1所示，半球壳谐振子中曲面一点的矢径为R，R在坐标系O－XYZ下的分量为Rsin αcos β，Rsin αsin β，Rcos α(其中R为矢量R的模).把经线和纬线作为坐标曲线α，β，它们的切线单位矢量e1，e2和法线单位矢量e3组成一个右手局部坐标系.假设半球壳的中曲面任一点在局部坐标系的位移为M=ue1+ve2+we3，法线方向上和此点距离为Z的一点的位移为MZ= uze1+vze2+wze3，假设变形后坐标系变为e'1，e'2，e'3，以θ表示在e1和e3确定的平面内，e3向e1的转角;φ表示e2和e3确定的平面内，e3向e2的转角;w1和w2分别表示在切平面内，e1向e2，e2向e1的转角.R为中曲面内一点变形前的矢径，P为同一点变形后的矢径，在局部坐标系下表示为基于基希霍夫－李亚夫假设，即薄壳变形前任何垂直于壳体中间表面的直线在变形后依然垂直于这一表面;沿壳体厚度的法线段的长度在变形过程中保持常值;在相邻的平行于中间表面的薄壳层表面间产生的法向应力与应力张量的其它分量相比是小量，可以忽略不计.再根据板壳理论、曲面论的知识和几何关系，得到半球谐振子中距离中曲面为Z的任一点的应变方程［5］为

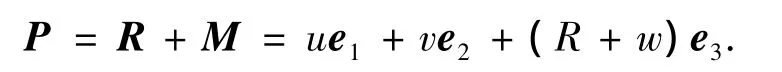
图1 半球薄壳一点的位移，变形及局部坐标系

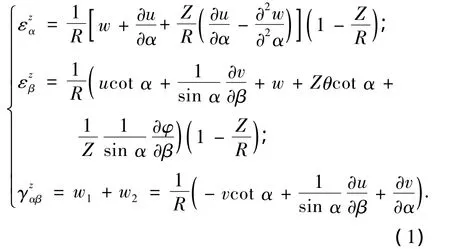
1.2 半球薄壳单元平衡方程

薄壳单元的应力分析如图2所示，可求出沿中曲面为单位宽度的面积上的内力.

在以α，β为法线的截面上，正应力分别为σα，σβ，切应力为ταβ，ταz，τβα，τβz.

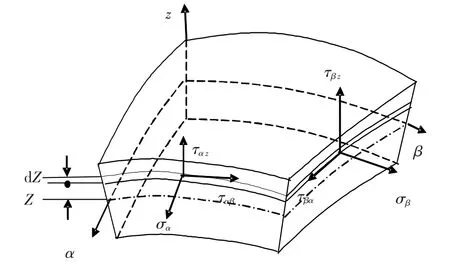
图2 薄壳单元应力图

图3为薄壳微元受力分析图，其中N1，S1，Q1，N2，S2，Q2为沿中曲面为单位宽度的面积上的内力，M1，M2，M12，M21为沿中曲面为单位宽度的面积上的力矩，q1，q2，q3分别是外力沿坐标系方向的投影，χ为扭率.根据面素的平衡条件建立力平衡方程，再求出其力矩平衡方程，从而得到半球薄壳单元平衡方程，如式(2)～(4)所示.

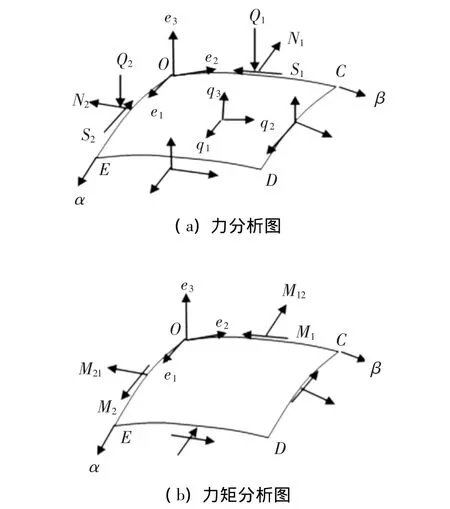
图3 薄壳微元受力图

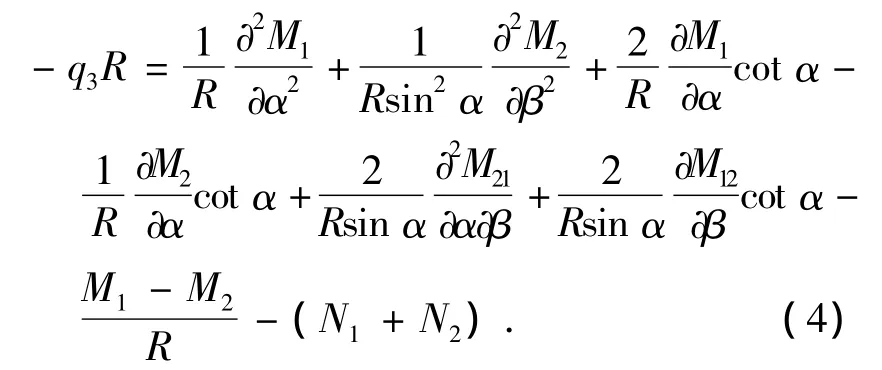
其中:

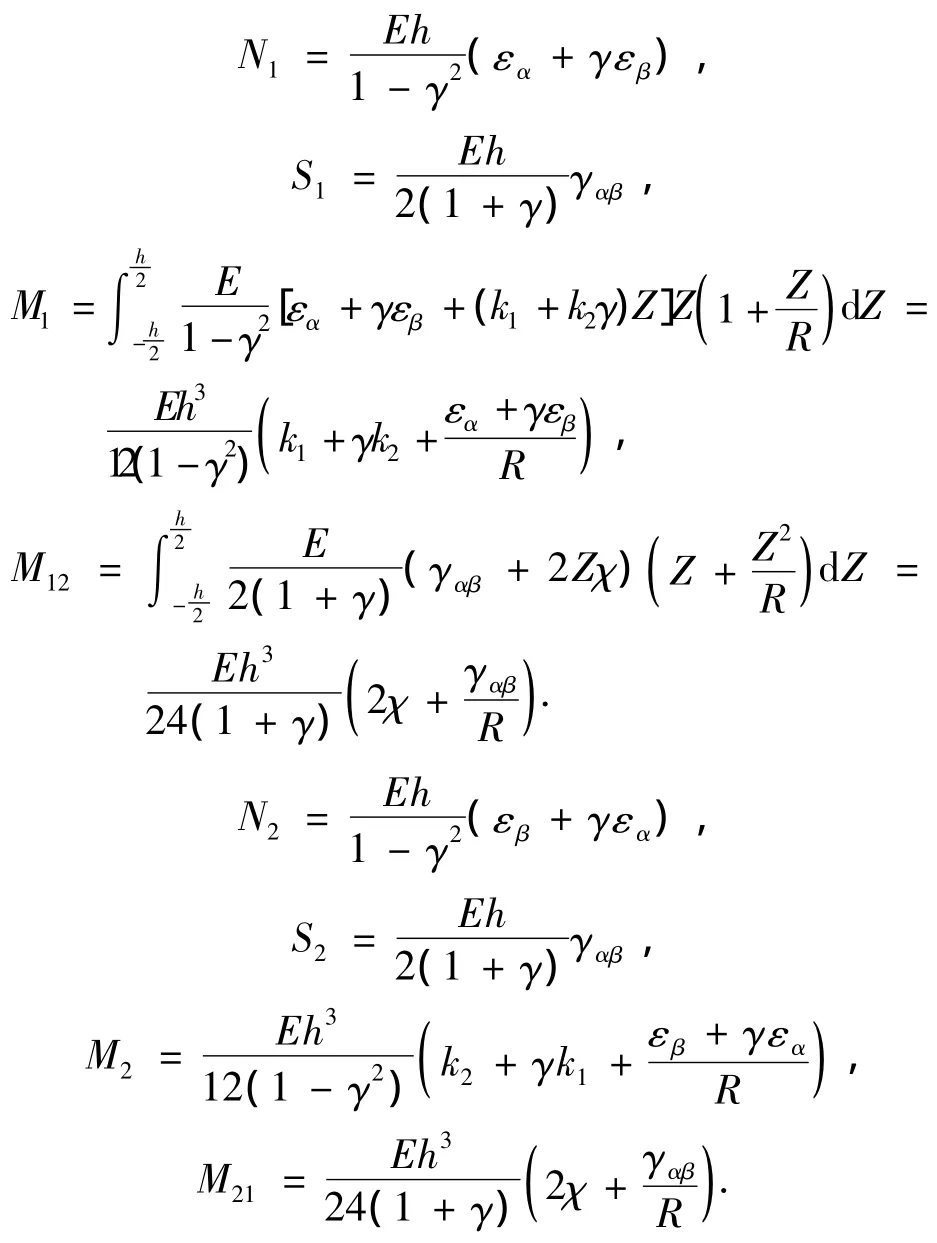
以下力平衡和力矩平衡方程的推导，可参照文献［6］.

1.3 半球谐振子二阶固有振型的动力学方程

在前面提到的半球薄壳单元平衡方程的推导过程中，在谐振的外力中必须考虑谐振子在惯性空间以角速度 [ΩxΩyΩz]T运动时的惯性力.根据哥氏定理计算得到谐振子的惯性力［X Y Z］T，并在时得

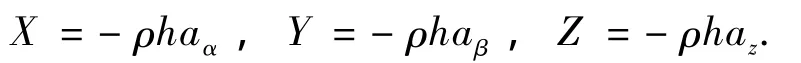
其中:ρ为谐振子的材料密度

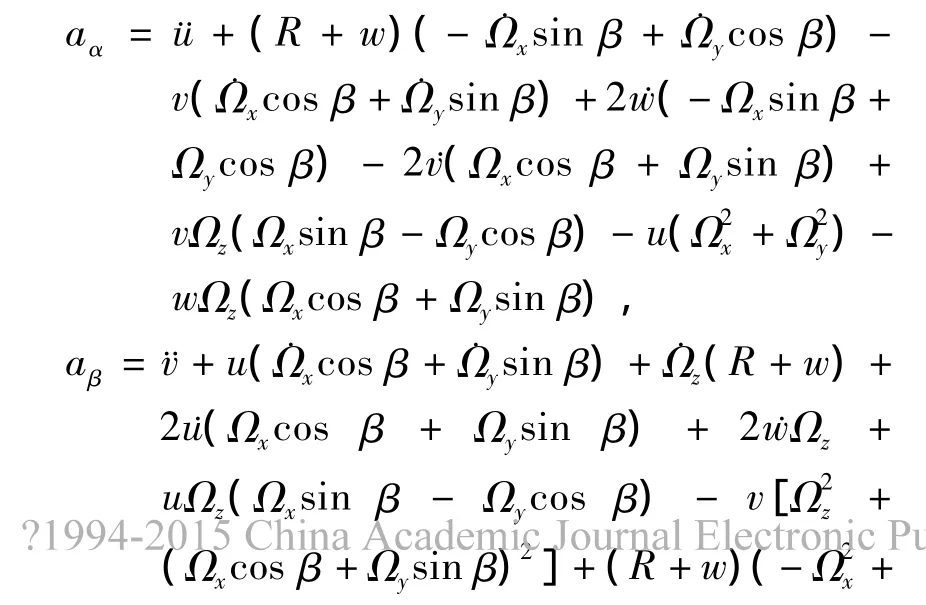
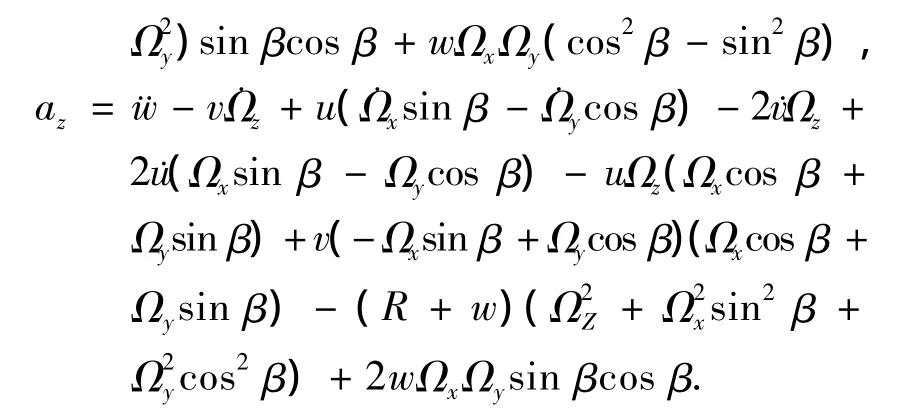
得到以角速率旋转并处于外分布载荷作用下的半球谐振子边缘的运动方程为

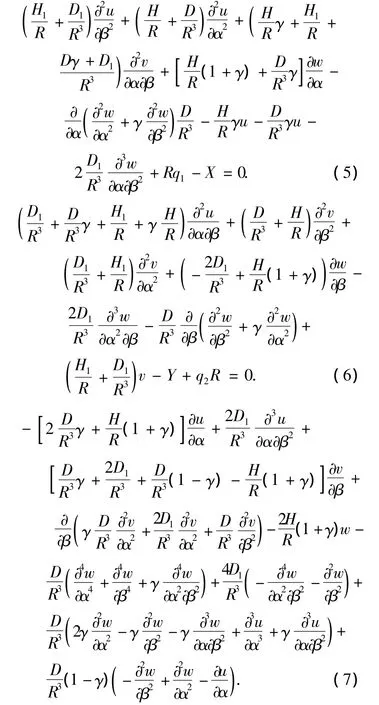
将谐振子各点的位移按不可拉伸薄壳的二阶固有振型展开得

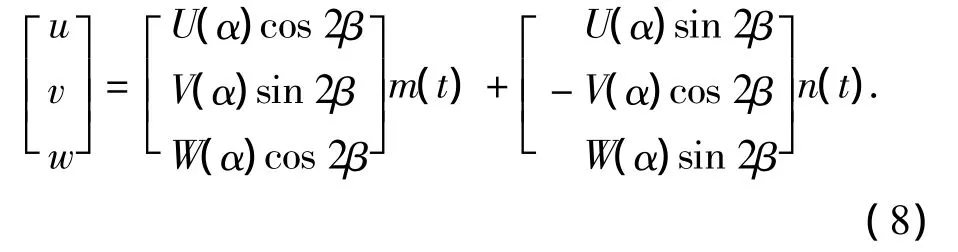
式中:

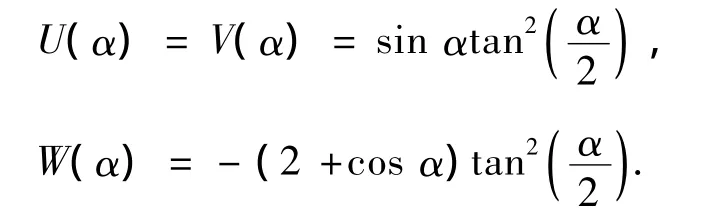
U(α)，V(α)，W(α)为半球薄壳二阶固有振型振动的瑞利函数，则半球谐振子边缘某点的位移方程为

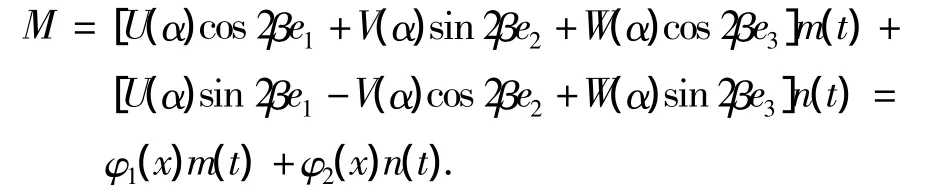
用Ax，Ay，Az分别表示式(5)～(7)的左边，则半球谐振子边缘的运动方程L可表示为

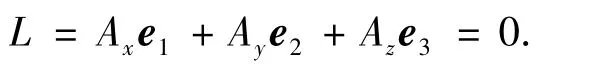
将式(8)代入式(5)～(7)并利用布勃诺夫－加廖尔金法［4］得

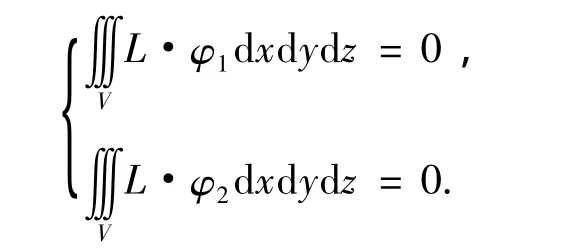
其中V为半球壳区域，化为球坐标

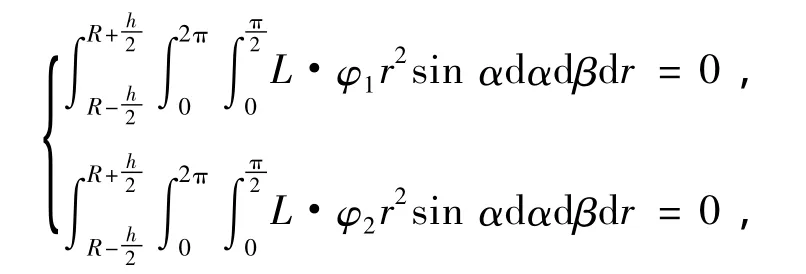
化简得

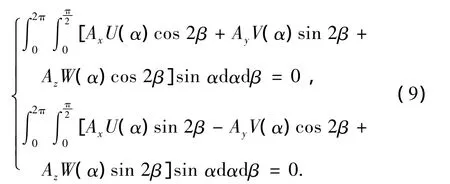
进行积分运算，可得动力学方程为

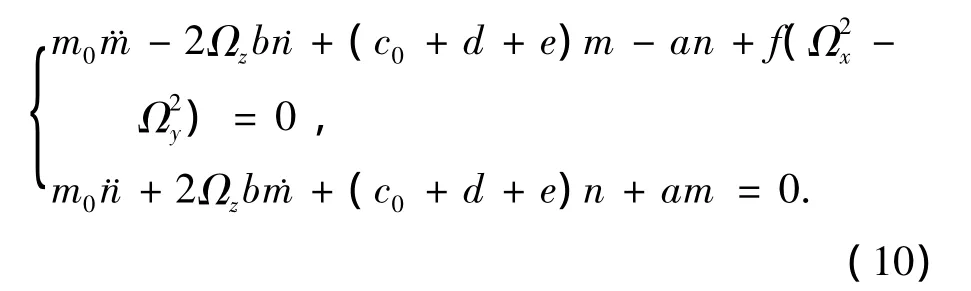
其中:

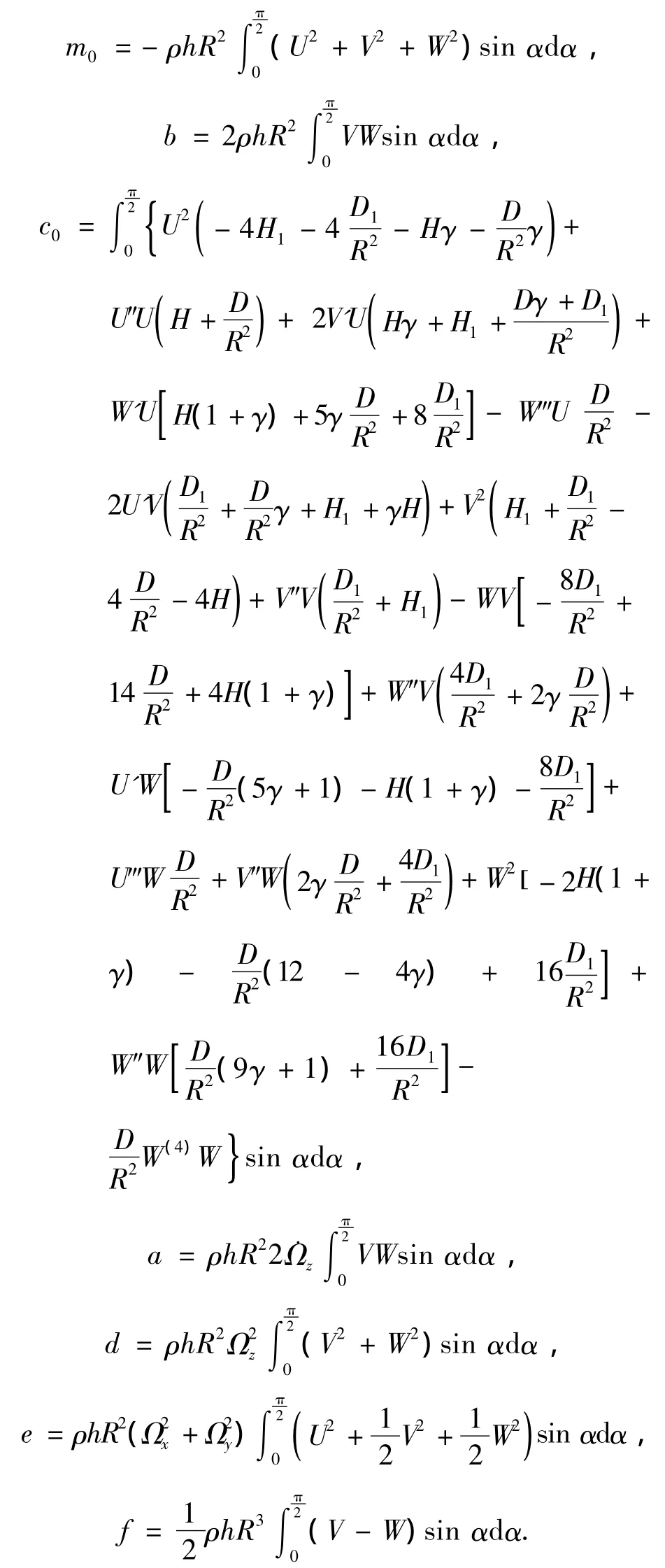
其中c0与文献［4］中的计算结果不同，增加了很多项，使谐振子的动力学方程更加精确，为进行半球谐振子运动机理分析及其质量，密度，厚度，杨氏模量等的不均匀性的误差分析打下基础.

下面与中电集团二十六所研制的半球谐振陀螺仪的实际参数进行计算比较.

2 固有频率的计算及比较

根据式(10)可知固有频率ω0的计算公式为

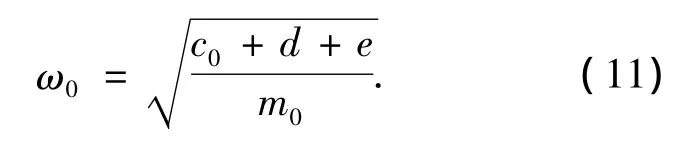
由U(α)=V(α)=sinαtan2(α/2)，W(α)=－(2+cosα)tan2(α/2)，对它们求取关于α的各阶导数U'(α)，U″(α)，U‴(α)及W'(α)，W″(α)，W‴(α)，W(4)(α)，然后代入c0，d，e和m0的公式中得

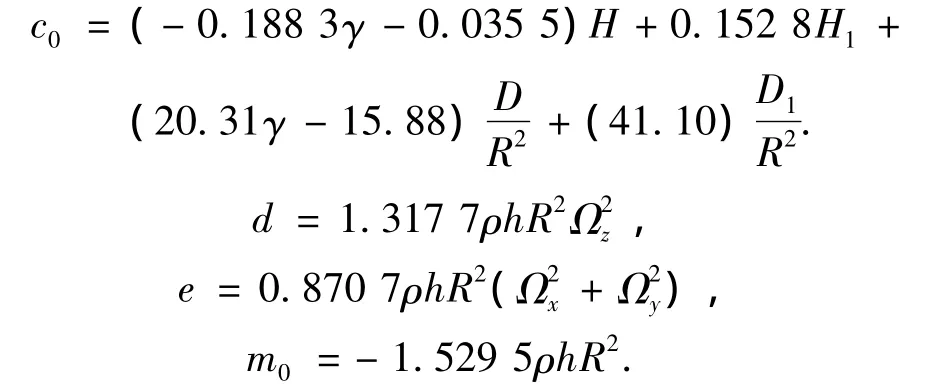
目前国内生产谐振子的材料为熔融石英，其密度ρ=2 200(kg·m－3)，杨氏模量E=7.67× 1010(N·m－2)，泊松比γ=0.17，它的几何参数为中曲面半径R=0.015 m，厚度h=0.85× 10－3m，将以上各值带入式(11)得:

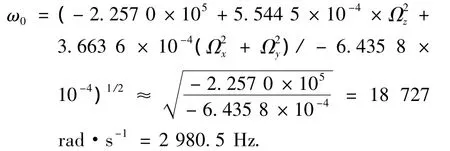
这与实际测量结果是一致的.而按照文献［4］给定的公式，计算结果为ω0=10 950 Hz，与实际不符.

文献［3］给定的参数为ρ=2 500(kg·m－3)，γ=0.17，h=10－3m，R=0.014 5 m，E=7.67× 1010(N·m－2)，按照本文的方法计算得 ω0= 2 623.6 Hz，半球壳支柱的长度和半径对固有频率影响较大［3］，故考虑支柱的影响后文献［3］计算结果为ω0=3 640 Hz，与本文的按完整半球壳计算的固有频率有一定的差别.按照文献［4］计算得ω0=10 622 Hz，此结果与实际严重不符，是不正确的.

3 结论

1)在建立半球谐振子的应变方程，力平衡方程的基础上得到了半球谐振子的动力学方程，比文献［4］中的动力学方程更加准确;

2)通过与有限元法计算的固有频率比较，证明了本文固有频率的计算公式的正确性;

3)通过实际的半球谐振陀螺仪的参数计算并与实际结果比较，证明了本文固有频率的计算公式及结果的正确性;

4)建立的半球谐振子动力学方程是今后半球谐振子的质量，密度，厚度，杨氏模量等的不均匀性的误差分析的基础.

［1］吕志清.半球谐振陀螺在宇宙飞船中的应用［J］.压电与声光，1999，21(5):349－353.

［2］EMILY L B，ALLAN Y L.In－flight characterization of cassini inertial reference units［C］//AIAA Guidance，Navigation and Control Conference and Exhibit.Hilton Head，South Carolina:AIAA，2007.

［3］杨倩.基于半球谐振陀螺的惯性导航系统研究［D］.哈尔滨:哈尔滨工业大学，2007:16－22.

［4］МАТВЕЕВ В А，ЛИПАТНИКОВ В И，АЛЕХИН А В. Проектирование.Волнового твердотелъного гироскопа［M］.［S.l.］:Издателъство МГТУ имени Н.Э.Баумана，1998:1－43.

［5］刘鸿文，林建兴，曹曼玲.板壳理论［M］.杭州:浙江大学出版社，1987.

［6］QI Jiayi，CHEN Xue，BEN Shunqing，et al.Dynamic error mechanism analysis of HRG［C］//ISSCAA2008.Shenzhen:［s.n.］，2008.

［7］梁嵬.半球陀螺仪谐振子振动特性及其结构研究［D］.长春:长春理工大学，2008:17－18.

［8］雷霆.半球谐振陀螺控制技术研究［D］.重庆:重庆大学，2006:9－10.

［9］ZHBANOV Y K.Vibration of a hemispherical shell gyro excited by an electrostatic field［J］.Mechanics of Solids，2008，43(3):328－332.

［10］ZHBANOV Y K，ZHURAVLEV V P.Effect of movability of the resonator center on the operation of a hemispherical resonator gyro［J］.Mechanics of Solids，2007，44(3):851－859.

［11］高胜利，吴简彤.半球谐振陀螺的漂移机理及其控制［J］.弹箭与制导学报，2008，28(3):61－64.

［12］FAN Shangchun，LIU Guangyu，WANG Zhenjun.On Flexural Vibration Of Hemispherical Shell［J］.Applied Mathematics and Mechanics，1991，12(10):1023－1030.