月面返回最优轨道设计
2010-03-24李罗刚崔祜涛马春飞毛春晓荆武兴
李罗刚,崔祜涛,马春飞,毛春晓,荆武兴
(哈尔滨工业大学深空探测基础研究中心,哈尔滨150080,llg0315@sina.com)
随着我国嫦娥探月计划三步走“绕、落、回”的顺利实施.月面返回技术成为我国月球探测计划必须先期解决的问题.在我国,目前对月球探测器软着陆最优轨道设计的工作比较多[1-3],但对月面返回最优轨道设计还是一片空白.而在国外,早在上个世纪60到70年代的阿波罗登月计划中,就已经成功将航天员送上月球并返回,在这个领域取得一定的成果[4-5].但是受限于当时控制理论限制,月面返回的控制方案还有待于进一步完善.当第二次月球探测高潮来临时,部分国外学者对这方面做了更深入的研究[6-9].大量的研究表明,对于共轭变量初值求解,一般除了特殊系统外,不可能求出最优控制的明确解析表达式,需要借助数值计算方法进行大量的迭代计算.求解的方法有很多,其中,打靶法由于其各种优点应用较多.但是,应用打靶法求解时需要首先猜测未知状态变量的初值,一旦猜测偏差过大,计算过程会陷入局部极值点或发散,在月球软着陆最优轨道的研究中已经有了一些可参考的成果.本文首先对有物理意义的量的初值进行猜测,通过解方程对共轭变量初值进行估计,辅助共轭变量初值的计算,用打靶法经迭代计算得到初始共轭变量的真值,然后将状态方程进行积分求得最优开环控制率.
1 动力学模型
探测器在进行月面返回时,直接进入一条100 km高度的圆轨道.这里尝试在三维空间中综合考虑月球自传、科里奥利力的影响,建立较为精确的动力学模型.
目前已发表的文献中探测器的动力学模型大多都是采用二维模型,即假设月球探测器在一个固定的铅锤面内运动,没有考虑侧向运动,而且所采用的模型都是在忽略月球自转的基础上得到的[1-2].由于在状态方程中必须利用位移矢量分量、速度矢量分量共6个状态变量实时表示从轨道坐标系到惯性坐标系转换所使用的欧拉角,如果采用普通的三次欧拉角旋转,欧拉角表示将会十分繁琐.文献[3]通过对坐标系巧妙的定义,使欧拉角化简到两个,实现了实时计算,但这样就把其探测器软着陆的初始轨道和终端位置都限定到白道面上,有一定局限性.
本文采用以初始轨道平面确定月心惯性坐标系的思想,即通过初始轨道平面在月球惯性空间中定义惯性坐标系的坐标轴,轨道坐标系的竖轴和惯性坐标系的两个坐标轴共面,使欧拉角转化为两个,即方便了计算,也使动力学模型没有局限性.
Ox1y1z1为轨道坐标系,原点在航天器,Oy1指向从月心到航天器的延伸线方向,Oz1延垂直于轨道平面方向,Ox1按右手坐标系规则定义.由于燃料的最优要求初始发射点在目标轨道平面内,即整个过程中,Oz1轴方向在月球惯性空间内保持不变.所以定义Oxyz为月心惯性坐标系,原点在月心,Oxy平面为月球赤道面,Oz轴指向月球北极,Oy轴延赤道面和Ozz1平面交线,Ox轴按右手系确定.Ox2y2z2为月球固连坐标系,原点在月心,Ox2y2平面为月球赤道面,Ox2轴指向初始时刻Ox轴与月面的交点,Oz2轴指向月球北极与Oz轴重合,Oy2轴按右手系确定.这样就使Oz轴、Oz1轴、Oy轴3个坐标轴处于同一平面上,如图1所示.
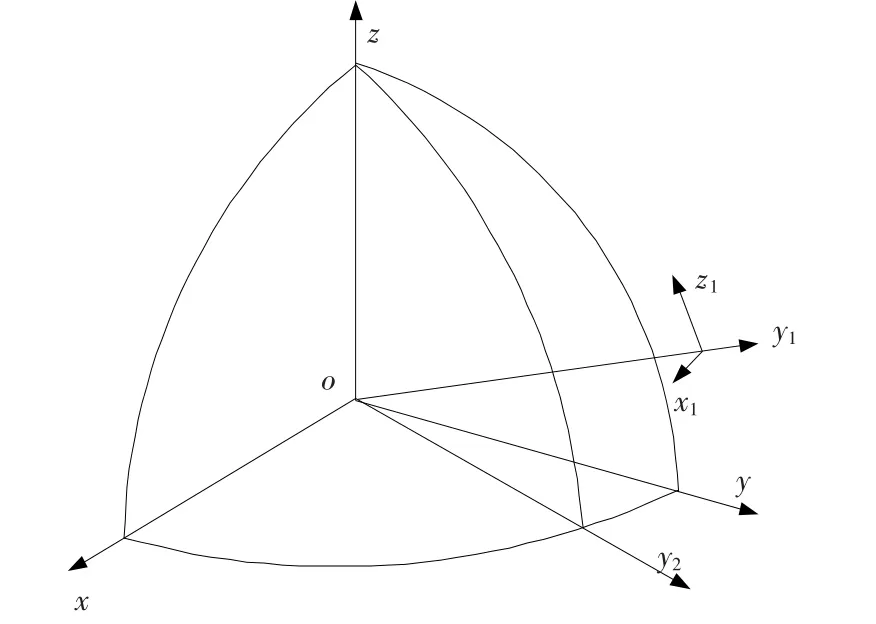
图1 坐标系示意图
发动机推力F的方向与探测器纵轴重合,θ是推力方向和Oy1的夹角.α是Ox1和Ox夹角,β是Oz1和Oz的夹角.γ为月固坐标系相对于惯性坐标系的转角.
因此,轨道坐标系到惯性坐标系的转换矩阵可表示为
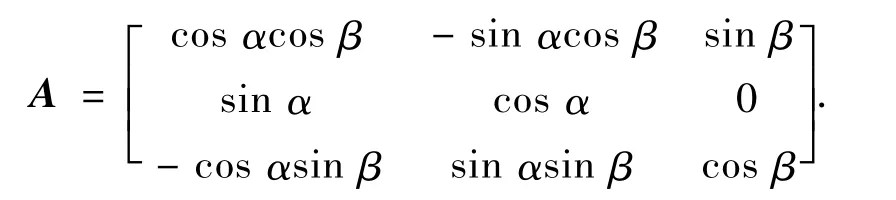
惯性坐标系到月固坐标系的转换矩阵可表示为

根据牛顿第二定律,得到探测器在惯性坐标系中的运动方程为

其中Vx,Vy,Vz为惯性坐标系中探测器的速度矢量分量;P为探测器发动机的秒耗量;E为它的比冲;m为探测器质量,m=mo-Pt;g为月球引力加速度.又由科里奥利加速度定理有
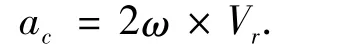
因此,航天器上升段在月球固连坐标系中的运动方程为

其中ω为月球自转速度;Vxl,Vyl,Vzl是航天器在月球固连坐标系中的速度.
2017年9月—2018年5月,选取哈尔滨医科大学第二临床医学院参加住院医师规范化培训的医学专硕研究生743名(2015级282人、2016级225人和2017级236人)。同时调查导师、轮转科室护士长和带教教师共210人。
2 燃料最优控制率设计
当达到预定轨道时,所剩质量最大,也就是消耗质量最小,即燃料最优,表达式如下:
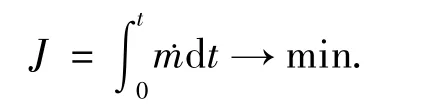
在动力上升段,当发动机推力恒定时,发动机的燃料消耗率就已经确定,因此性能指标就变为飞行时间最小,飞行时间越小,燃料消耗也就越少,即
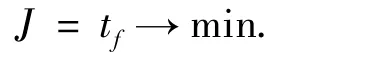
取系统状态变量为
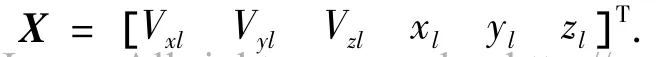
其中xl,yl,zl为月球固连坐标系中的坐标.系统状态方程表示如下:

其中:θ是控制变量,μ是月球万有引力常数;aij(i,j=1,2,3)定义如下:
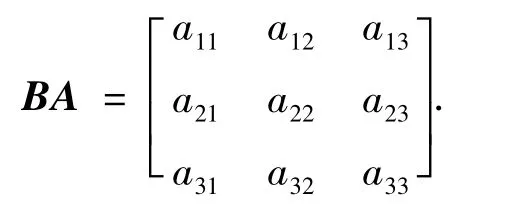
取共轭变量为
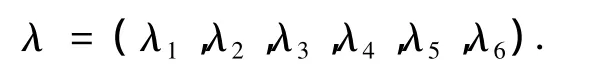
构造汉密尔顿函数如下:

燃料最优就是要找到一组容许的控制,调整推力的方向,使探测器飞行时间最小.根据极大值原理,设控制量取值范围不受限,得到极值条件
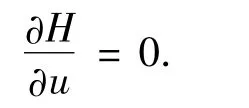
因此,所得到的最优控制率为

共轭方程为

3 终端约束
月面返回动力上升段初始条件静止,各个状态变量都为零.终端条件是要使之进入指定环月轨道,终端时刻tf自由.需要满足一定的终端条件:1)速度向量达到一定约束条件.2)位移向量达到一定约束条件.3)速度向量与位移向量方向垂直.4)速度向量和位移向量都在预定轨道平面内.因此得到的终端约束集为
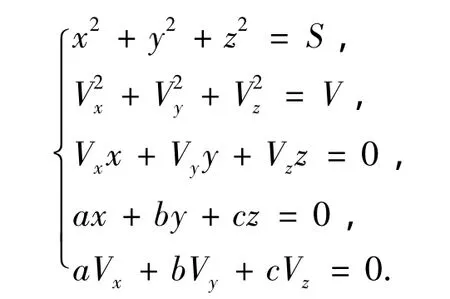
横截条件为

其中ξ是拉格朗日乘子,将最优控制率带入状态方程和共轭方程,利用初始条件进行积分,即可得到月面返回最优轨迹,此时最优轨道的求解就转化成两点边值问题的求解.注意:终端约束集中,速度、位移各个分量都是指在惯性坐标系中,进行计算时要通过惯性坐标系和月球固连坐标系转换矩阵转换.
4 最优控制问题求解
选取动力返回时终端指标函数
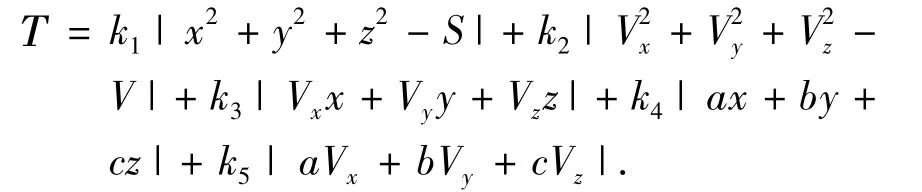
其中kn(n=1,2,…,5)为加权系数.根据初始时刻推力方向垂直向下,即θ=0,可得到λ1λ2λ3初始值对应比例关系,大大方便了计算.利用matlab编程,以共轭变量为参数,通过优化λ极小值终端目标,最终得到一组满足终端约束条件的共轭变量初值.用求得的共轭变量初值和系统状态变量初值进行积分,即可得到一条月面返回最优轨迹.
5 算例及仿真结果
设探测器初始质量为6 000 kg,定常推力发动机推力15 000 N,比冲3 000 m/s,初始速度为0,航天器初始位置北纬6°,东经26°.并设目标轨道是一条100 km高的圆形环月停泊轨道.另外,初始时刻,γ=0,α,β通过状态变量的值进行实时计算.可求得共轭变量初值如下:
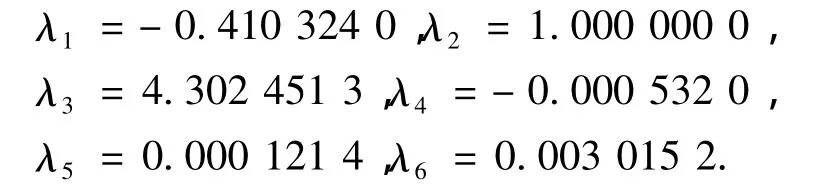
经过仿真计算,求得推力方向角度、终端约束指标、质量随时间的变化曲线,如图2所示.
由于月球是逆时针旋转的,可以看到推力方向角由零开始逐渐负向减小.也就是说,探测器沿月球自转方向顺行发射.终端约束指标在850 s左右时达到极小值,几乎为零,也就是进入了预定轨道.最终消耗掉探测器一多半质量燃料,得到最优轨迹如图3所示.
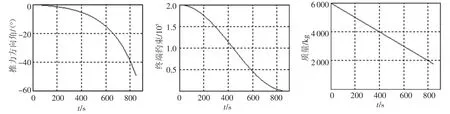
图2 最优控制率及终端约束指标
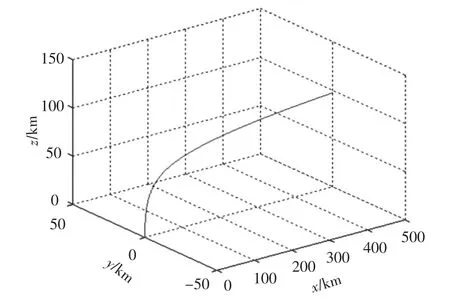
图3 月面返回动力上升段最优轨迹
最终得到的最优轨道终端参数分别为
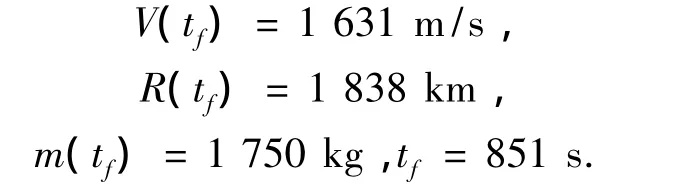
6 结论
在月球探测器月面返回问题研究中,综合考虑月球自转,科里奥利力的影响,建立探测器在三维空间中的较精确动力学模型.利用Pontryagin极大值原理,基于燃耗最优的原则,设计月面返回最优控制律.在数值计算中,采用打靶法,以共轭变量初值为参数,以月面返回动力上升段终端状态为优化指标,综合考虑位置和速度约束,通过参数优化,得到了满足终端约束的一组共轭变量初值,同时得到了探测器月面返回的最优轨迹,可以较高精度的实现探测器月面返回,对于我国探月三期工程具有实际工程应用参考价值.
[1]王大轶,李铁寿,马兴瑞.月球最优软着陆两点边值问题的数值解法[J].航天控制,2000,(3):44-49.
[2]徐敏,李俊峰.月球探测器软着陆的最优控制[J].清华大学学报,2001,41(8):81-89.
[3]周净扬,周荻.月球探测器软着陆精确建模及最优轨道设计[J].宇航学报,2007,28(6):1462-1471.
[4]ARMSTRONG E S,SUDDATH J H.Application of pontryagin maximum principle to the lunar orbit rendezvous problem[R].Langley Station,Hampton,Virginia,USA:NASA Langley Research Center,1963.
[5]ARMSTRONG E S,CHILDS A G,MARKOS A T.A method for computing extremal maximum-range thrustlimited rocket trajectories with application to lunar transport[R].[S.l.]:NASA,1970.
[6]MIELE A,WANG T,MANCUSO S.Optimal free-return trajectories for moon missions and mars missions[J].The Journal of the Astronautical Sciences,2000,48 (2):183-206.
[7]THORNE J D,HALL C D.Minimum-time continuousthrust orbit transfer[J].The Journal of the Astronautical Sciences,1997,45(4):411-432.
[8]WILSON J W,SIMONSEN L C,SHINN J L,et al.Radiation analysis for the human lunar return mission[R].Langley Station,Hampton,Virginia,USA: NASA Langley Research Center,1997.
[9]RYAN P,RUSSELL,CESAR A.Geometric analysis of free-Return trajectories following a gravity-assisted flyby[J].Journal of Spacecraft and Rocket,2005,42(1): 138-151.
