有限域上基于Gr¨obner基的高级综合优化方法

王冠军，赵 莹，王茂励

(1.中国矿业大学计算机科学与技术学院，江苏徐州，221116，zywgj@cumt.edu.cn;2.山东省计算中心，济南250014)

根据美国半导体协会制订的2005年国际半导体技术发展路线及其在2006年的更新，未来15年集成电路仍将按摩尔定律持续快速发展.预计到2010年，高性能CPU芯片上可集成的晶体管数目将超过20亿个(到2018年超过140亿个)，片上局部时钟频率可达到 15GHz (到2018年超过53 GHz)，Intel总裁Craig Barrett预测说，传统的芯片制造技术有可能支撑到5 nm的范围［1］.半导体技术的这些进步，使单个芯片上集成更复杂和更灵活的系统成为可能.半导体技术的迅猛发展的主要原因是:1)需求牵引;2)技术驱动.这也促使芯片的设计技术在越来越高的层次上进行，高级综合应运而生，各种综合的方法和优化技术也不断出现.本文是在电路的多项式符号代数表示基础上，在有限域上通过多项式的各种运算，进行综合优化.Gr¨obner［2］基主要用来做理想成员判定和代数方程求解，在本文中主要用于域上多项式分解和多项式最大公因式(GCD)的计算方面，在库单元映射方面也有重要应用.

1 有限域代数与Gr¨obner基

1.1 有限域代数

以素数P为模的整数剩余类环构成P阶有限域GF(P).在任何P阶有限域中能找到一个生成元素a，它能生成域中所有P－1个非0元素，从而构成一个循环乘群G(a):1，a，a2，…，ap－2，ap－1=1.域中非0元素所构成的乘法群之阶定义为域中该元素的级.有限域的元素个数是素数.可以定义两类有限域，GF(P)和它m度的扩展GF(Pm).基本域GF(P)中包含元素{0，1，2，…，p－1}，最小的域是GF(2).它的加法操作相当于电路异或操作而乘法操作则相当于与操作.

定义1(多项式环) 假定F为有限域，域上以x为变元的多项式为

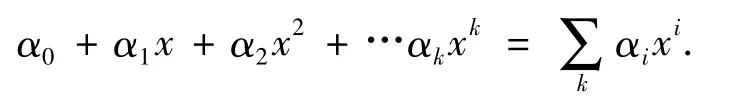
式中:∀αi∈F，αi为系数，k为阶.αk称为首项系数，如果αk=1，则称多项式为首一多项式，域上所有以x为变元的多项式组成一个多项式环F［x］.相似的定义F［x1，x2，…，xd］=A，表示域上d个变元的多项式环.当F=GF(2m)时，相应的多项式则以2m为模.

1.2 Gr¨obner基

域k上的关于x1，…，xn的全体多元多项式的集合记为k［x1，…，xn］，容易验证k［x1，…，xn］对于多元多项式的加法与乘法运算构成一个含有单位元的交换环，称之为多项式环.

定义2 设F={f1，…，fl}为一个多元多项式集合.由F生成的理想记为I=＜F＞:

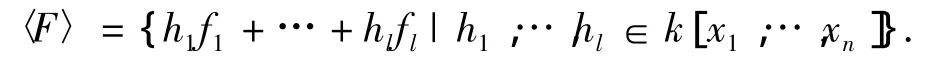
多项式F={f1，…，fl}称为生成该理想的基，由于F是有限的，故称该理想是有限生成的.Hilbert基理论证明了任何一个理想都是有限生成的.

定义3 给定了Nn上的一个可容许的排序 ＞，设f∈k［x1，…，xn］，定义为

1)f的multidegree为

multideg(f)=max(α∈Nn:aα≠0).

2)f的首项单项式为

LM(f)=Xmultideg(f).

3)f的首项系数为

LC(f)=amultideg(f).

4)f的首项为

LT(f)=LM(f)LC(f).

定义4 设多项式 r∈ k［x1，…，xn］，F= {f1，…，fs}⊆k［x1，…，xn］－{0}为环k［x1，…，xn］中零多项式的有限集合.若r=0或者r模F不能约化，即LT(fi)，i=1，2，…，s，中任一项都不是r中所出现的各项的因子，则称多项式r对F是既约的，记为进而，若，则称r为f相对F的余多项式.

定义5 设I是环k［x1，…，xn］上的一个非零理想，G={g1，…，gs}是I中非零多项式的有限集合，称G是理想I的Gr¨obner基，当且仅当对于I中的每个非零多项式f，存在gi∈G使得LT(gi)|LT(f).

定义6 设f，g∈k［x1，…，xn］－{0}，L= lcm(LM(f)，LM(g)).其中，lcm为最小公倍式.令.称多项式S(f，g)为f和g的S－多项式.

定义7 称环k［x1，…，xn］中的Gr¨obner基G={g1，…，gs}是既约的，用RGB表示，若对于所有的i，1≤i≤s为:

1)LC(gi)=1.

2)gi相对于G－{gi}是既约的，即gi中没有非零项可以被任何LM(gj)，j≠i，除.

可以证明一个理想的既约Gr¨obner基唯一.

2 有限域上高级综合优化

将Gr¨obner基理论应用到了数据通路的综合中.L={l|l为元件库中元件的多项式表示}.为了使用元件库中的元件构建多项式s所表示的数据通路，一个必要条件是:s∈＜L＞.为了检验s是否为 ＜L＞中的元素，首先需要计算出 ＜L＞的Gr¨obner基G，然后执行除法算法Reduce(s，G)，设若r=0，则s为 ＜L＞中的元素;更进一步，若∀i，ui，gi∈L，则该数据通路可以用元件库中的元件来构建.

综合算法中同时引入了高层次重构技术和对多项式的一些基本操作(加/减、乘法、除法、倒置等)及传统的算术电路设计中的代数变换技术，例如词 －重写技术［3］、因式分解［4］、树高度缩减［5］、Horner形式与提取公因式［6］、系数的模块与分段、分解与扩展、代数冗余消除等，从而实现了基于最少器件数、最小时延等不同目标的数据通路优化.优化的目标是产生表示不同但功能相等的结果.

2.1 多变元多项式分解

目前不少符号计算软件都提供因式分解的函数完成多元多项式的分解这种计算.本文将GOPALAKRISHNAN［7］RTL级缩减算法改造应用在行为级分解中，并给出有限域上的多变元多项式分解算法.

1)待分解多项式f，有限域F(2m);

2)x1，x2，…，xd为多项式中d个变元;

3)SF(n)=k为n整除k!(n|k!);

4)Yk(x)=x(x－1)…(x－k+1)称为降阶乘积方程;

5)Yk称为降阶乘积方程在多变元多项式中推广;

6)μi定义为:μi=min{2ni，SF(2m)};i=1，2，…，d.

域上多变元多项式分解算法的程序为:

算法核心思想是将多元问题转化为一元问题来解决.算法首先计算SF(2m)，然后利用它计算μi值.找出多项式每个变量的最大度数ki，利用Yui分解多项式，将余数作为新的多项式，重新计算ki和Yui，Yui～Y0循环分解.分解后，进行判断:

1)如果quo可以为两多项式相乘形式，且余数为0，结束;

2)如果quo可以为两多项式相乘形式，且余数为不为0，将余数作为新多项式继续分解;

3)如果系数ck＞bk，将除数定义为bk·Yk，将余数作为新多项式继续分解.

2.2 有限域上基于既约Gr¨obner基的GCD计算

Gr¨obner基应用广泛，既约Gr¨obner基在有限域上针对多项式符号代数表示电路在最大公因子提取方面的应用.最大公因子(GCD)提取是多项式分解等操作的基础，其中给出几个相关性的定义为: A=k［x1，x2，…，xn］为域k上n变元多项式环.

定义8(消元序) 设X1和X2是变元x的幂积，Y1和Y2是变元y的幂积.定义为

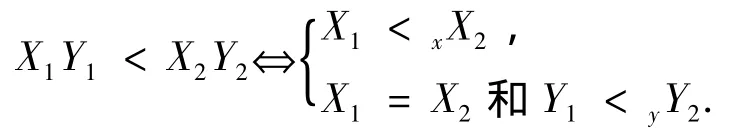
容易验证，定义的序 ＜是项序，则称这个项序为x变元大于y变元的消元序.

定理1(消元定理) 令I是域k上环k［y1，…，ym，x1，…，xn］中的非零理想，项序 ＜是x变元大于y变元的消元序，令G={g1，…，gt}是理想I的Gr¨obner基，则G∩k［y1，…，ym］是理想I∩k［y1，…，ym］的基.

由于有限域上的多项式环A=k［x1，x2，…，xn］是唯一因子分解整环，该环中的任何2个多项式都有最大公因子.但是，环k［x1，x2，…，xn］，n≥2，不是主理想环，更没有欧几里得除法算法，因此要计算最大公因子非常困难，本文应用消元理论解决，给出算法GCD-RGB为:

步骤1 假设f，g∈k［x1，x2，…，xn］.

步骤2 令d=gcd(f，g)为f，g的最大公因子(lc(d)=1)，d由f和唯一确定.

步骤3 计算l=lcm(f，g)为f，g的最小公倍，其中，lc(l)=lc(f).lc(g).

步骤4 得到 f.g=lcm(f，g)gcd(f，g)＜lcm(f，g)＞=＜f＞∩＜g＞.

步骤6 在环k［x1，x2，…，xn，ω］中相对x变元小于ω变元的消元序计算理想 ＜ωf，(1－ω)g＞的既约Gr¨obner基G，再求G∩k［x1，x2，…，xn］.由于G∩k［x1，x2，…，xn］={lcm(f，g)}，即lcm(f，g)就是G中ω变元不出现的那个多项式.由于G是＜f＞∩ ＜g＞的既约Gr¨obner基，用除法算法可得到h，使得fg=h.lcm(f.g)，于是计算出gcd(f，g)=h.

2.3 库单元映射

现代高层次设计的输出常常需要映射到组件库中，在这种情况下，库单元映射成为支撑高层次设计的有效手段.在本文中库单元映射的输入为数据通路的多项式表示和库单元的多项式表示，输出则为数据电路全部映射为库单元中的基本电路模块.给出库单元映射方法为:

输入:数据通路的多项式表示

库单元的多项式表示

输出:电路模块是否可映射

算法中假设数据通路可分解为k个多项式，通过以上算法就可以判定给定数据通路多项式是否可映射，首先计算待替换数据路径中电路的特征多项式，然后从元件库中寻找基本电路模块并计算其Gr¨obner基，最后进行比较判断，如果所有的多项式模块都可映射为元件库中单元，那么就可以进行替换的工作.库单元映射通常有基于最少元件数映射和基于最小关键路径延迟映射等方法.本文给出考虑多目标约束的映射方法，方法基于整数线性规划(ILP)模型，每个数据通路多项式可以由一个或多个库单元构成，其目标函数为

式中:约束条件分别为组件数，面积，关键路径延迟(CPD)和功耗时延积(PDP).给出一组映射如图1所示.

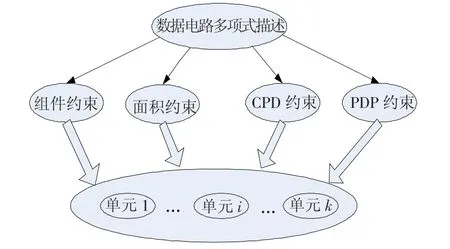
图1 基于多目标约束的库单元映射

当目标函数和各约束条件生成之后，就可以利用成熟的ILP工具来解决，使用ILP交集解法并最终得到映射方案.这种方法简单易行，时间复杂度亦在可以允许的范围内，因此是有效的.

3 实验验证

多项式表达式出现在许多现实的应用中，例如数字信号处理和3D图形图像领域.为便于比较，实验环境设置如文献［7］中所示，输入多项式的综合只用加法器与乘法器来构建完成.应用Synopsys Design compiler工具(时钟周期40 ns，工作电压5 V，1.0 μ power2－sample.db技术库)估计加法器和乘法器的面积和延时.面积和延时的估计结果如表1所示，其中的加法器和乘法器均为16 bit.实验中用到的多项式集合如表2所示，本实验选取了7个多变元多项式，多项式因式分解的结果如表3所示，其中，CPD为电路中关键路径延时.

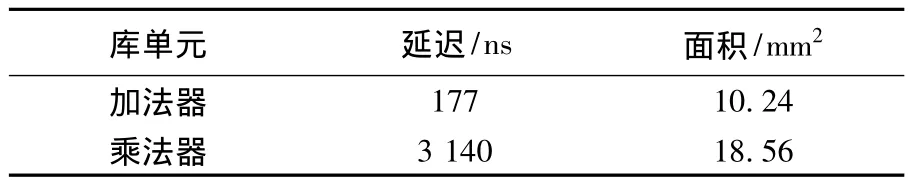
表1 库单元的延迟和面积

表2 多项式实验电路

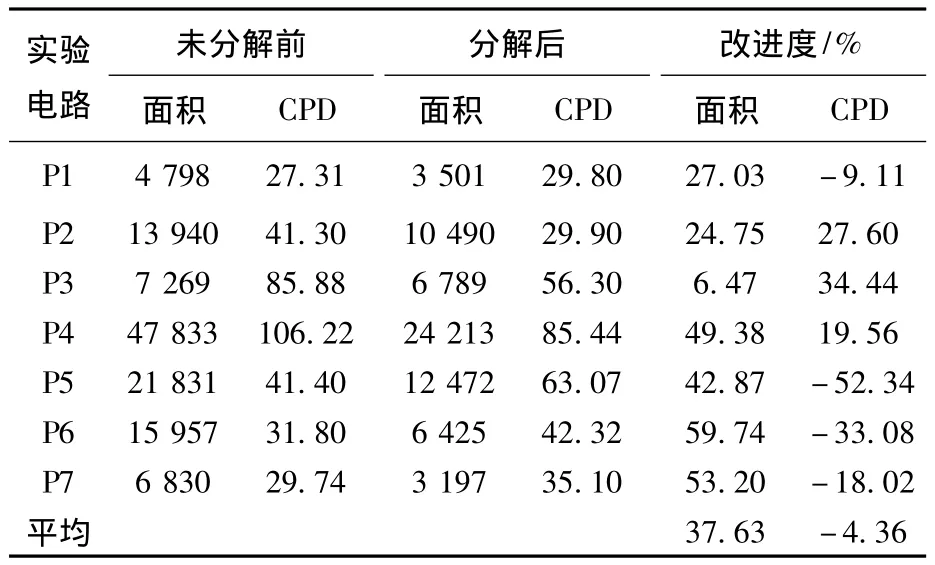
表3 多项式分解的综合实验结果

从表3的实验综合结果来看，域上多项式分解可以有效的降低芯片面积(平均减少37.63%)，但与此同时会带来CPD的少许增加(平均增加4.42%)，这是因为多项式的分解会使一个较大的多项式变为几个小的多项式，减少了优化延迟的机会，因此使CPD出现了少许增加，要解决这个问题，可以通过增加代价函数的方法来进行折衷.

库单元映射方法本文选取了一些典型的实验电路，在各种约束下得到的映射结果如表4所示，从采用基于ILP模型的交集解法得到映射结果来看，最高的改进达到 23.3%，平均改进达到14.6%.

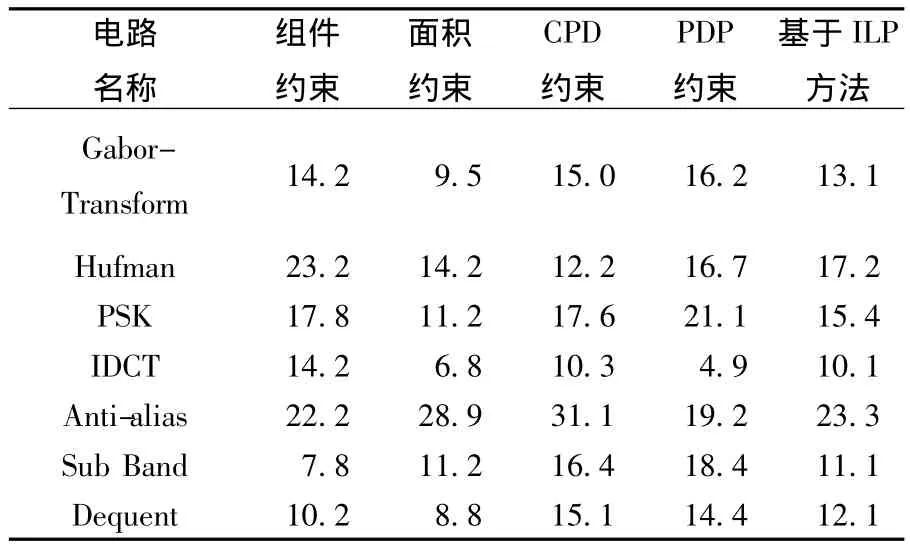
表4 典型电路的库单元映射结果 %

4 结论

1)文献［8－10］给出了多项式优化的一些最新的研究成果，这也表明了多项式符号代数的生命力，在此基础上的有限域多项式优化仍将是一个较新的研究方向.

2)由于多项式规模对Gr¨obner基的计算有重要影响，因此在优化过程中需要考虑计算复杂度问题.

［1］安虹.用可重构计算技术实现高效能通用微处理芯片［J］.信息技术快报，2006，4(6):11－34.

［2］BUCHBERGER B.An Algorithm for Finding a Basis for the Residue Class Ring of a Zero-dimensional Polynomial Ideal(in German)［D］.Austria:University of Innsbruck，1965.

［3］ARVIND，SHEN X W.Using term rewriting systems to design and verify processors［J］.IEEE Micro，1999，19(3):36－46.

［4］HOSANGADI A，KASTNER R，FALLAH F.Energy efficient hardware synthesis of polynomial expressions［C］//Proceedings of the 18th International Conference on VLSI Design held jointly with 4th International Conference on Embedded Systems Design.Washington: IEEE Computer Society，2005:653－658.

［5］MANGALAM G N，NARAYAN S，van BESOUW P，Avra.Graph transformations for improved tree height reduction［C］//Proceedings of the 16th International Conference on VLSI Design.Washington:IEEE Computer Society，2003:474－479.

［6］HOSANGADI A，FALLAH F，KASTNER R.Optimizing polynomial expressions by algebraic factorization and common subexpression elimination［J］.IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems，2006，25(10):2012－2022.

［7］JABIR A M，PRADHAN D K，MATHEW J.An Efficient technique for synthesis and optimization of polynomials in GF(2m)［C］//Proceedings of the 2006 IEEE/ ACM international conference on Computer-aided design.New York:ACM，2006:151－157.

［8］XING Xianwu，JONG ChingChuen.Using symbolic computer algebra for subexpression factorization and subexpression decomposition in high level synthesis［C］// Proceedings of the IEEE International Symposium on Circuits and Systems(ISCAS).Japan:IEEE，2005: 5645－5648.

［9］WANG Jian，JIANG Anping.An area-efficient design for modular inversion in GF(2m)［C］//Proceddings of the IEEE Asia Pacific Conference on Circuits and Systems (APCCAS).Singapore:IEEE，2006:1496－1499.

［10］JING M H，CHEN J H，CHEN Z H，et al.Low complexity architecture for multiplier inversion in GF(2m)［C］//Proceddings of the IEEE Asia Pacific Conference on Circuits and Systems(APCCAS).Singapore:IEEE，2006:1492－1495.