混凝土多孔砖砌体墙的开裂性能实用解析研究
2010-03-24孟广伟尹新生
李 妍,孟广伟,尹新生
(1.吉林大学机械科学与工程学院,长春130022;2.吉林建筑工程学院寒地绿色建筑技术工程研究中心,长春130118,lessle@tom.com)
随着我国墙体材料改革和节能政策的贯彻执行,混凝土多孔砖成为我国大力发展的替代粘土砖的主导产品之一.但是混凝土多孔砖作为一种新型的墙体材料,其砌体结构在施工和使用过程中普遍存在着裂缝问题,而裂缝的存在,不仅影响结构的正常使用,而且对其抗震的性能有较大的影响[1-2].所以如何对裂缝进行控制,使其在安全使用的许可范围内,防止或减少裂缝带来的危害就变得尤为重要.目前对砌体结构中裂缝(群)相互作用及其破裂问题的研究,大多集中在结构试验研究阶段[3],文献[4-5]对不同荷载作用下砌体结构的性能进行了实验研究,并得出了滞回曲线;文献[6-7]对砌体结构在轴力、弯矩作用下的性能进行了研究,提出了抗弯、抗剪承载力的计算公式.但总体上说,砌体破坏机理的研究无论是国外还是国内主要是集中在假设模型的基础上的静力性能分析和利用有限元提出一些简化模型对砌体的性能进行研究[8-9].而有关混凝土多孔砖墙破裂模式的研究,由于所处理破坏问题的复杂性,很难对其从变形、破裂全过程进行模拟.
自Kaplan首次将断裂力学应用于混凝土以来,准脆性材料的断裂理论[10-11]分析日益成为国内外专家学者的研究热点之一.但是由于砌体材料复杂的开裂机理,寻找并建立适用于砌体裂缝扩展的断裂准则、新的断裂参数以及相应的计算方法,长期以来在国内外却鲜有报道.本文基于固体力学和线弹性断裂力学基本原理,运用修正的剪滞理论[12-13],考虑到建立模型的方便和计算结果的精确设置了三个变异层,结合能量法则推导出了混凝土多孔砖砌体墙的等效断裂韧度的计算模型[14]:针对相关的试验数据,分析了对应标准子层高为1,2,3,4,5 mm各组模型的等效断裂韧度,通过对结果的比较分析,提出了适合计算的合理的标准子层高,同时验证了等效断裂韧度是与试件尺寸无关的断裂参数,从而为研究混凝土多孔砖砌体墙的开裂与破坏的预测预报提供了新的方法,在工程上具有较强的适用性.
1 剪滞分析模型
根据混凝土多孔砖砌体墙的实际受力情况,建立如图1所示的墙体模型,假定上下表面受均布压力q的作用,厚度为t,高度为h,含初始裂缝长度为a0.为研究裂缝扩展中的应力重分布,建立图2所示分层剪滞模型,即将模型沿着其高度方向划分为n个子层,其中无裂缝砖区、无裂缝砂浆区、裂缝区、无裂缝砂浆区、无裂缝砖区(详见图3)的子层数分别为p+1、q、r+1、s和np-q-r-s-2层,各子层的标准高度为为了计算方便,将每层砖的第1子层,每层砂浆的第1子层分别设为具有特殊高度的子层,其子层高度分别为db0,dm0,这样就可以使得模型中不能整除的部分加到这几个特殊高度的子层上,即设置变异层.为了更为合理地设置各区子层高度,将裂缝区中间层设置为变异层,其子层高度为d0.
假定每一子层在垂直y方向的截面上仅有正应力,上下表面仅有切应力,则各子层的位移ui应该仅为x的函数(沿x轴正向为位移的正向).取长为dx的第i子层的微段,其受力如图4所示.
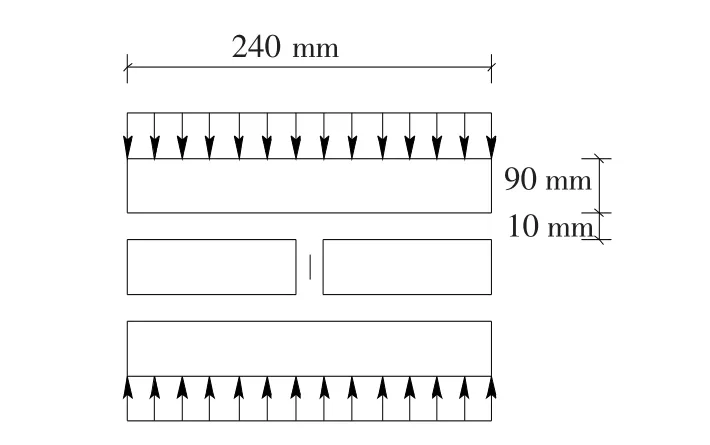
图1 混凝土多孔砖砌体墙模型及受力分析图

图2 基于竖向灰缝的分层剪滞模型

图3 基于竖向灰缝扩展的有限子层剪滞模型

图4 第i子层微段的受力图
其中:qi(x)为子层轴向压力,pi(x)为由横向变形对纵向变形的影响引起的相应子层轴向拉力,τi-1(x)和τi(x)分别为上下层间切应力.令第i子层的水平位移为ui(x),竖向位移为vi(x).砖和砂浆的应力-应变关系均采用双线性关系,通过切应力来考虑砖和砂浆在分界处变形的相互影响,可以分别写出砖和砂浆的pi(x)及τi(x)的表达式.
砖的表达式为
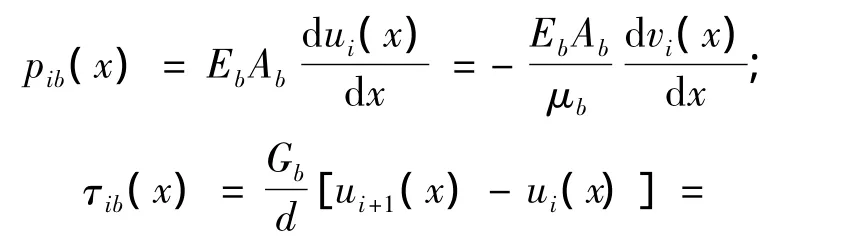

砂浆的表达式为

式中:Eb和Gb、Em和Gm分别为混凝土多孔砖和砂浆的弹性模量和切变模量;A=td为子层截面面积,其中d为标准子层厚度.
利用横向变形与纵向变形的关系式
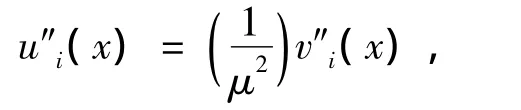
可以列出所有子层微段的剪滞平衡方程.
可见,第1至p+1子层微段的剪滞平衡方程组为

其中:A1=tdb0,列出第p+2至p+q+1子层微段的剪滞平衡方程组为

其中:A2=tdm0,需要注意的是,为便于利用对称性计算,在采用本计算模式时,中间裂缝区的子层数r应该为偶数.在一个砖厚的砂浆裂缝区中,由于断裂处的砂浆应力为零,所以该区剪滞方程中弹性模量和泊松比均取自砖,即第p+q+2至p+ q+r+2子层微段的剪滞平衡方程组为

其中:A0=td0,同理,可得到各子层微段的剪滞平衡方程.
2 剪滞方程的求解
为便于求解,考虑引入无量纲参数,并根据相应的边界条件来求解上式的n阶非齐次线性方程组,从而得到各子层的位移分布,则各子层的正应力为

在ξ=0处,裂尖最邻近子层的拉伸应力集中因子则由下式求得:

采用有限子层模型模拟裂缝扩展,假设裂缝扩展长度a'为标准子层高度,无裂缝区第p+q+ 1层在x=0处的正应力为σp+q+1(0),则该混凝土多孔砖墙应变能释放率(即裂缝扩展单位长度系统应变能的下降值)为

由线弹性断裂力学可知,在平面应力条件下,

3 等效断裂韧度的确定
由式(1)—(3)得到该混凝土多孔砖砌体墙等效断裂韧度的解析表达式为


4 试验结果与分析
该试验采用吉林省祝焰新型建材有限公司生产的KP1型混凝土多孔砖,其材料配比分别为:水泥:18%;粉煤灰:19%;煤矸石:11%;中砂: 17%;5~10 mm的碎石:35%,并按照 GB/T 2542—2003的测试条件及要求测得该批砖的强度等级的平均值为fbm=12.3 MPa,材料常数Eb=1.65×104MPa,μb=0.22;吉林亚泰集团鼎鹿牌水泥配制的水泥砂浆,测得其强度等级的平均值为 fmm=9.6 MPa,材料常数 Em=0.4× 104MPa,μm=0.25,11个试件的尺寸分别为:5个L1系列(长度为240 mm),3个L2系列(长度为490 mm),3个L3系列(长度为740 mm),其基本参数及荷载值如表1所示.
根据本文所建立的基于竖向灰缝模型的有限子层剪滞模型,对该模型所划分的层数和层高如表2所列.利用有限元软件ANSYS,在表3中列出了按本文计算的对应标准子层高d分别为1,2,3,4,5 mm的等效断裂韧度KC的解析解及由试验所得到的数值解.
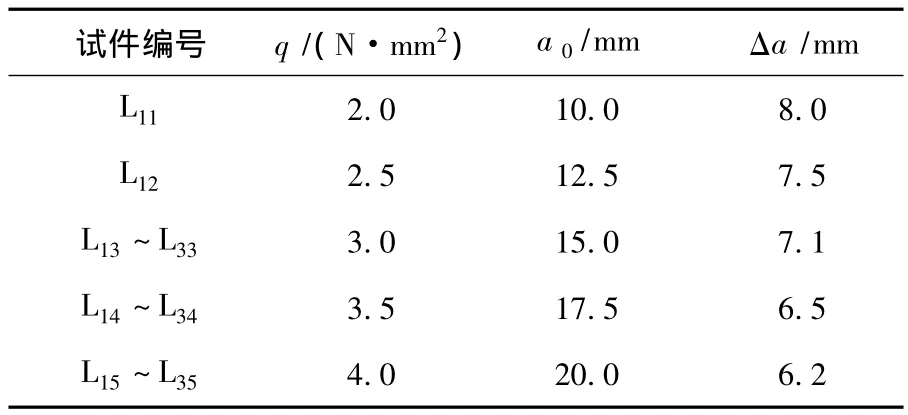
表1 试件的基本参数及荷载值

表2 有限子层剪滞模型的基本参数

表3 混凝土多孔砖砌体墙等效断裂韧度的计算值 MPa·m1/2
由表3可以得出,d分别为1,2,3,4,5 mm时,KC的平均值分别为0.302 8,0.301 7、0.300 6、0.300 0、0.299 1、0.301 8 MPa·m1/2,KC的均方差分别为0.010 1、0.010 3、0.010 6、0.010 0、0.009 8,KC变异系数分别为0.033 3、0.034 1、0.035 3、0.033 3、0.032 8.而实验所得到断裂韧度的平均值、均方差、变异系数分别为0.301 8 MPa·m1/2、0.011 5、0.038 1.
可见,混凝土多孔砖砌体墙的等效断裂韧度是一个不随试件尺寸变化的材料常数,可以作为控制其断裂的材料参数.而且,用本文方法计算的同一试件的等效断裂韧度存在随层数增多而逐渐增大的趋势,这是因为本文假设的裂缝扩展长度为标准子层高,随着层数的增加,标准子层高逐渐减小,使得应变能释放率逐渐趋于零.
5 结论
1)基于竖向灰缝模型推导出了求解混凝土多孔砖砌体墙等效断裂韧度的解析计算模式,并通过相关实验进行了数值分析,可知:同相关试验对应的数值解相比,解析解的均方差和变异系数更小,因此本文所建立的求解混凝土多孔砖砌体墙等效断裂韧度的解析计算模式具有很好的鲁棒性,是求解其等效断裂韧度的一种新的、实用的解析计算方法.
2)从理论上验证了基于竖向灰缝模型的混凝土多孔砖砌体墙等效断裂韧度是一个与试件尺寸无关的断裂参数.
3)通过分区设置变异层可以使得所建立的剪滞分层模型更加方便和精确,从而为剪滞理论在砌体断裂力学中的推广应用提供了理论依据.
4)揭示了标准子层的层高是控制剪滞分层模型分析混凝土多孔砖砌体墙等效断裂韧度的计算敏感性的一个重要因素,建议标准子层高度取为3~5 mm,这样既能够简化计算,又能够保证取得理想的计算精度.
[1]门进杰,史庆轩,周琦.竖向不规则钢筋混凝土框架结构基于性能的抗震设计方法[J].土木工程学报,2008,41(9):67-75.
[2]杨伟军,林立,杨春侠.混凝土多孔砖砌体房屋抗震可靠度分析[J].工程力学,2007,24(10):100-104.
[3]王凤来,李新.配筋砌块短肢砌体剪力墙偏压承载力试验[J].哈尔滨工业大学学报,2008,40(10):20-24.
[4]MIHA T,NIGEL C,SHIVAS S.Seismic behavior of masonry walls:experimental simulation[J].Journal of Structural Engineering,ASCE,1996,122(9):1040-1047.
[5]ABRAMS D P,PAULSON T J.Modeling earthquake response of concrete masonry building structures[J].ACI Structural Journal,1991,88(4):475-485.
[6]CHIOU Y J,TZENG J C,LIOU Y W.Experimental and analytical study of masonry infilled frames[J].Journal of Structural Engineering,1999,125(6):1109-1125.
[7]ALSHEBANI M M,SINHA S N.Stress-strain characteristics of brick masonry under uniaxial cyclic loading[J].Journal of Structural Engineering,ASCE,1999,125 (6):600-604.
[8]XING Jingtang,PRICE W G,CHEN Yigen.A numerical method to simulate nonlinear fluid-rigid structure interaction problems[J].Acta Mechanica Solida Sinica,2005,26(4):373-383.
[9]王述红,孙豁然.砌体受压开裂过程数值模拟及其力学特性研究[J].哈尔滨工业大学学报,2006,38(4): 644-648.
[10]吴智敏,王金来,徐世烺.基于虚拟裂缝模型的混凝土等效断裂韧度[J].工程力学,2000,17(1):99-104.
[11]徐世烺,周厚贵,高洪波.各种级配大坝混凝土双K断裂参数试验研究——兼对《水工混凝土断裂试验规程》制定的建议[J].土木工程学报,2006,39 (11):50-62.
[12]CARPINTERI A,CORNETTI P,BARPI F.Cohesive crack model description of ductile to brittle size-scale transition:dimensional analysis vs.renormalization group theory[J].Engineering Fracture Mechanics,2003,70:1809-1839.
[13]曾庆敦.复合材料的细观破坏机制与强度[M].北京:科学出版社,2002.
[14]王铎.断裂力学[M].哈尔滨:哈尔滨工业大学出版社,2006.
