速率系数可变模型的建立及其性能研究

袁一星，钟 丹，侯秀琴，赵洪宾，P.M.R.Jonkergouw，S.T.Khu，D.Savic

(1.哈尔滨工业大学城市水资源与水环境国家重点实验室，哈尔滨150090;2..哈尔滨工业大学市政环境工程学院，哈尔滨150090，zhongdan2001@163.com;3.School of Engineering，Computer Science and Mathematics，University of Exeter，Exeter，EX4 4QF，UK)

维持管网中一定质量浓度的余氯是保障供水管网水质的一项重要措施，因此，氯衰减规律的预测及模拟一直是国内外研究的热点［1－3］.目前，氯衰减模型包括一级模型、二级模型、n级模型、限制一级模型及平行一级模型等［4－5］.也有研究者采用经验法来建立氯衰减模型［6－9］.然而上述氯衰减模型均不能用同一组参数准确预测任意初始氯质量浓度和二次加氯质量浓度条件下氯的衰减情况.针对这种局限性，提出一种半经验数学模型:速率系数可变模型(Variable Rate Coefficient，VRC).

1 模型的建立

管网中的氯可以同时与水中多种物质发生反应，这些反应之一可表述如下:

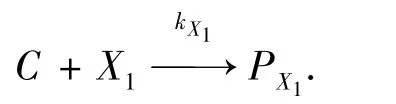
式中:C为氯，X1为水中一种与氯反应的物质，kX1为速率常数，PX1为该反应的消毒副产物.

假设氯和X1都是一级反应，则氯及X1的衰减速率可表示为

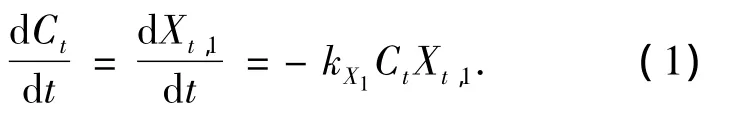
式中:Ct为t时刻氯的质量浓度，Xt，1为t时刻X1的质量浓度.

假设氯在主体水中的消耗由n个这样的反应引起，则氯的衰减速率为

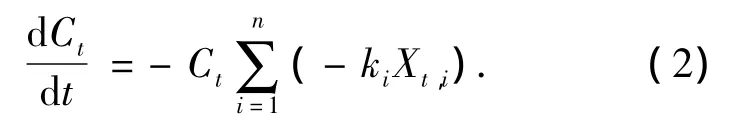
式中:Xt，i为t时刻水中第i个与氯反应的物质的质量浓度，ki为反应速率系数，其他同上.

由式(3)可以看出，除速率衰减系数用平均速率衰减系数κt表示外，式(3)与式(1)表达形式基本一致.此外，式(3)可用来确定某时段κt的变化，即在已知Ct，Xt和κt初始值条件下，可以直接计算出某时段氯质量浓度的变化及Xt，从而使预测氯的衰减问题转化为定义一个函数来表述κt的变化.

由于κt的初始值只取决于各反应的反应速率系数和各种反应物质量浓度之比，且κt趋近于全部ki中的最小值(非零)，则由 κt=及每种反应物的衰减速率可得到κt的微分方程:

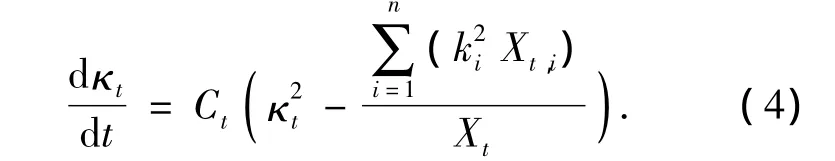
对式(4)进行简化，可得到下列近似方程:

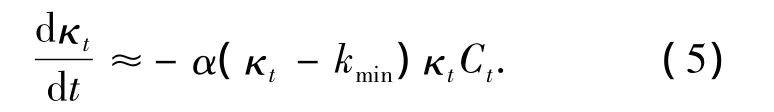
式中:α为无量纲因数;kmin为κt的最小值.

本研究用方程(3)和(5)作为给水管网中主体水氯衰减的数学模型.

2 实验

2.1 实验方法

实验用水取自哈尔滨某水厂未加氯的出厂水，实验在5 d内完成以防水质发生较大变化.氯质量浓度使用Hach和Hanna(HI－95711)便携式测氯仪进行测定.

2.2 模型校核

VRC模型需要用4个参数进行校核:X0，κ0，kmin和α.其中，X0为所有与氯产生反应的物质质量浓度组合(mg/L)，其仅在水样稀释或浓缩时变化;κ0和kmin仅与温度有关;α为无量纲系数.

方程(3)中的两个未知数(X0和κ0)存在无数组组合，这些组合具有相同的拟合度，其真实值难以确定，但已知X0至少应达到烧杯实验最大的需氯量，因此，可首先在一定范围内确定X0，而后再在该范围内校核其余3个参数.κ0，kmin和α的校核采用复合形混合演化算法(Shuffled Complex Evolution，SCE法)，该算法结合了单纯形法、随机搜索、生物竞争进化以及混和分区等方法的优点，将生物自然演化过程引入到数值计算中，通过模拟生物进化的过程来提高计算效率和全局搜索整体最优的能力，因此，可一致、有效、快速地搜索到模型参数全局最优解［10－12］.在校核模型参数的同时，还应调整输入VRC模型中的初始氯质量浓度(对于二次加氯情况，还应调整二次加氯后的初始氯质量浓度)以减小模型预测值和实测值之间的差距.输入模型中的初始氯质量浓度并不是指最初的投氯量，也不是指第一次测定的氯质量浓度，而是对第一次测定的氯质量浓度(投氯后10～15 min左右测得的质量浓度)进行优化调整后的数值.这是因为本模型假设开始预测时氯已与水完全混合，而在实际中，氯投加到水体后，会由于混合不均、局部质量浓度过高等原因在最初的一段接触时间内迅速衰减，所以，有必要对初始氯质量浓度进行调整，其调整的幅度主要与第一次测定的时间和温度有关.输入VRC模型中各初始氯质量浓度的最优值通过局部搜索法确定.

2.3 目标函数

模型优化的目标是为了使模拟值和测定值之间残差平方和(ESS)最小，即

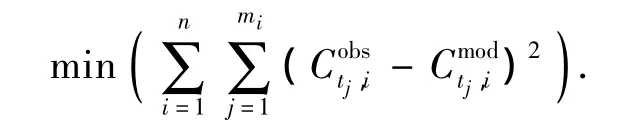
式中:n为校核时使用的数据集数，mi为对于数据集i的氯质量浓度测量次数，C和C分别为数据集i、t时刻、第j次氯质量浓度的测定值和模拟值，包括t=0时刻的数值.

适于一次加氯和多次加氯的优化步骤如下: 1)首先确定X0的值，κ0、kmin和α的值由SCE法得到;2)使用局部搜索法，调整初始氯质量浓度，减小ESS;3)对于每次二次加氯:a.从第2)步起由模型预测确定二次加氯时的Xt和κt值，参数κ0和kmin恒定;b.对于每组二次加氯数据集，使用局部搜索法，调整二次加氯质量浓度，使ESS最小.每次加氯实验都要重复上述步骤.为保证结果的稳定性和重现性，每次均需进行3组独立的校核，每组校核是随机的且初始氯质量浓度不同.计算Ct，Xt和κt变化的时间间隔设为1 min.

3 结果与讨论

为使模型适用范围更广，在3.5，15.5，28℃温度条件下分别进行了3组独立的烧杯实验(共9组).当余氯质量浓度达到0.1～0.3 mg/L时，对5组进行二次加氯.模型性能的评价采用本实验的数据(HRB)和Boccelli等人的实验数据(HLW、TX、OH、NV和CT)［2］.

3.1 模型性能分析

对于HRB(28℃)数据集，校核后ESS随X0的变化如图1所示.

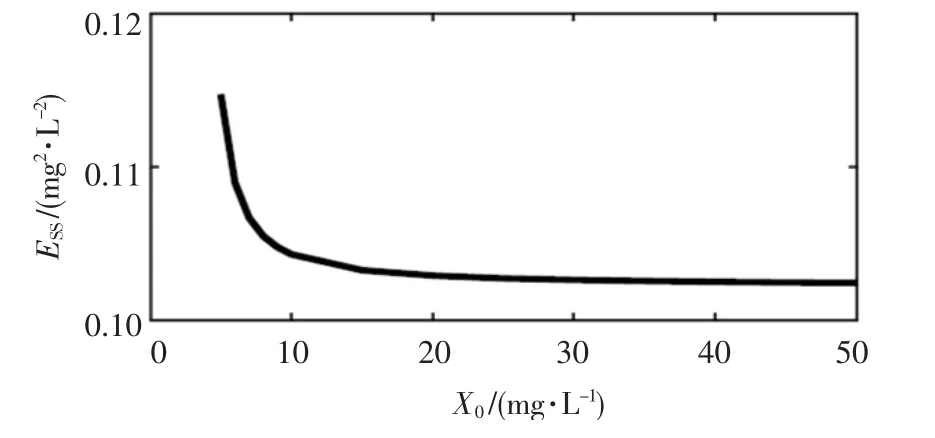
图1 校核后ESS随X0的变化(HRB 28℃)

由图1可以看出，当X0＜10 mg/L时，ESS值变化较为剧烈.而后，随着X0值增加，ESS值变化逐渐趋于平稳.当X0＞30 mg/L时，ESS值基本稳定在0.103左右.尽管赋予较高的X0估值可得到较小的ESS值，进而得到更可靠的预测结果.然而随着X0估值的增大，α值也会随之增大，κt在第一个时间段内可能产生负值，从而导致模型不稳定(特别是对初始氯质量浓度较高的情况).因此，本研究中将X0取30 mg/L，在这一条件下，6组数据集均可得到较稳定的结果和较好的拟合度.

表1所示为包括VRC模型在内的3种模型校核后的参数以及各模型的均方根误差(ERMS).其中，各模型均分别使用同一组参数来进行拟合.由表1可知，对于HRB数据集，与预期相反的是κ0值没有随温度升高而升高，其最高值出现在15.5℃条件下.这可能是由于在不影响模型准确性的前提下，调整了输入模型的初始氯质量浓度，却没有考虑κt在最初一段时间的衰减情况导致的.

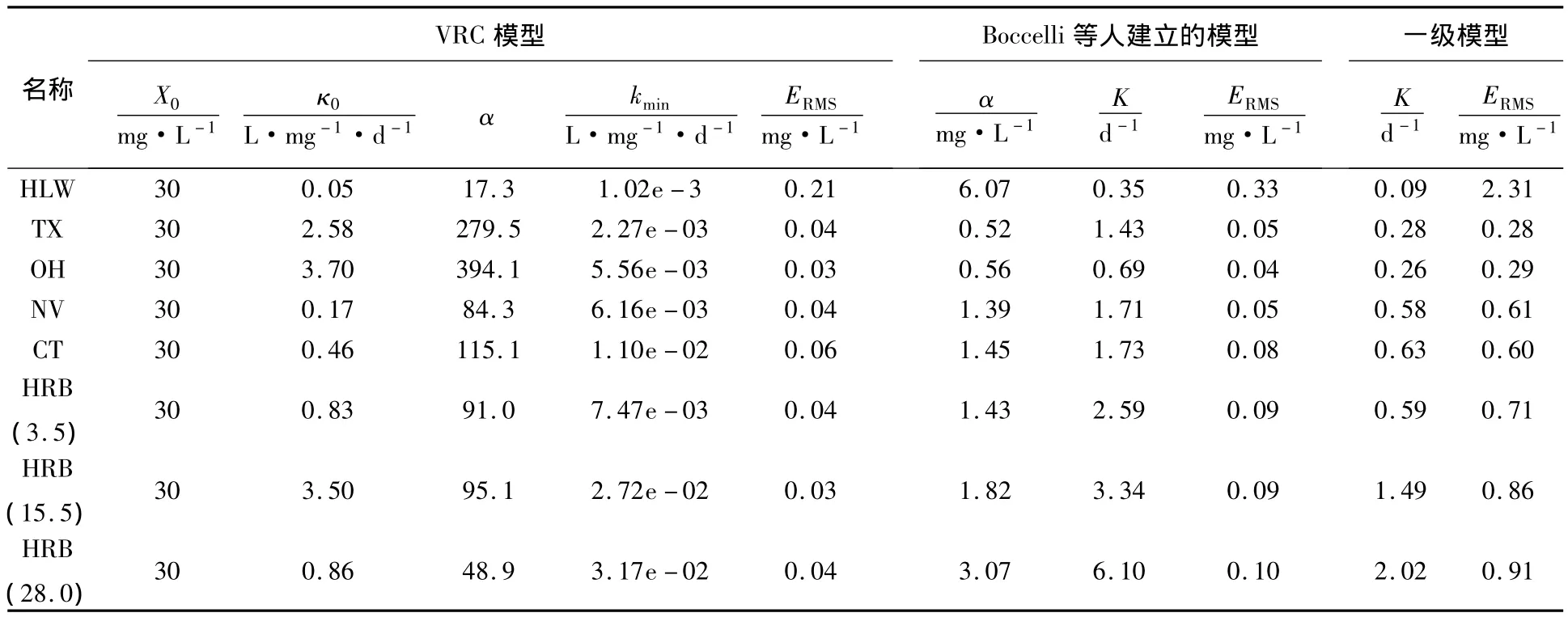
表1 校核后的参数及模型误差

对于HLW数据集，用VRC模型和Boccelli等人建立的模型拟合氯衰减情况，其中一组结果如图2所示.可以看出，VRC模型可以用同一组参数较为准确地拟合所有情况下的氯衰减过程，而Boccelli等人建立的模型则存在一定的偏差.

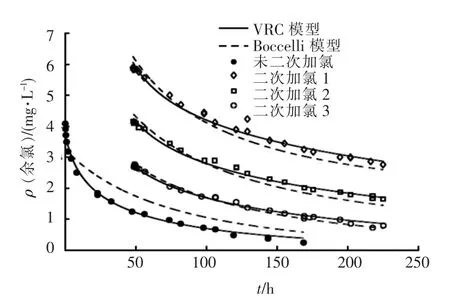
图2 用VRC模型和Boccelli模型拟合氯衰减(HLW)

3.2 模型可靠性

VRC模型的可靠性用模型校核时未使用的数据集进行评价.例如对于HRB数据集，首先选取3组数据中的任意2组数据进行参数κ0，kmin和α的校核，剩余1组数据用来评价模型可靠性;而后重新选择3组数据中的2组数据(数据组不得重复)进行再次校核，以判断模型的可靠性是否取决于数据集的选择.试验中X0设为30 mg/ L，同时调整输入模型的氯质量浓度.对于Boccelli等人模型的可靠性评价采用同样的方法，结果如图3所示.

图3 用VRC模型和Boccelli模型预测氯衰减(HRB)

由图3可见，VRC模型可以准确地预测氯的衰减过程.但对图1C，若时间间隔仍设为1 min，则κt在第一个时间段内的衰减值比κ0大，从而导致κt产生负值，这可能是由于校核时使用的氯质量浓度数据(1A和1B)比验证数据低造成的.因此，时间间隔需由1 min缩短至1 s.

对HRB(15.5℃)数据集，即使用氯质量浓度较高的两组数据(2B和2C)来进行校核，VRC模型仍具有较高的可靠性.这表明VRC模型良好地描述了水中氯衰减的动力学过程.同时也表明，校核VRC模型时，最好使用至少1组初始氯质量浓度较高的数据集.对于HRB数据集，不同温度下平均速率系数κt随时间的变化如图4所示.

图4中3条曲线的绘制均使用表1所列的模型参数值，且输入模型的初始氯质量浓度均为2.00 mg/L.由图4可见，在初始阶段κt值并没有随温度升高而升高，而15 min后温度越高κt值越高.同时可知，VRC模型可以使用具有一定误差的初始氯质量浓度来预测氯的衰减过程，但调整该输入值，模型的性能会得到进一步改善.

图4 不同温度下κt随时间的变化

4 结论

1)提出了一种新的氯衰减模型——VRC模型，该模型基于双分子二级反应动力学速率方程(式(3))，同时定义了一个微分方程(式(5))来描述κt随时间的变化，通过二者结合来模拟氯的衰减过程，模型包含X0，κ0，kmin和α 4个参数.

2)采用6组氯衰减数据集对VRC模型、一级模型以及由Boccelli等人建立的二级模型进行校核.实验结果表明:VRC模型对所有数据集的拟合情况均明显优于另外两个模型，可以更准确的预测氯的衰减过程.

3)校核VRC模型时最好使用至少1组初始氯质量浓度较高的数据集，以保证模型的稳定性.在校核模型参数的同时，还应调整输入VRC模型中的初始氯质量浓度以减小模型预测值和实测值之间的差距.

［1］ MUNAVALLI G R，MOHAN K M S.Water quality parameter estimation in a distribution system under dynamic state［J］.Water Research，2005，39:4287－4298.

［2］ COZZOLINO L，PIANESE D，PIROZZI F.Control of DBPs in water distribution systems through optimal chlorine dosage and disinfection station allocation［J］.Desalination，2005，176:113－125.

［3］ CLARK R M，HAUGHT R C.Characterizing pipe wall demand:Implications for water quality modeling［J］.Journal of Water Resources Planning and Management，2005，131:208－217.

［4］ HAAS C N，KARRA S B.Kinetics of microbial inactivation by chlorine－I:Review of results in demandfree systems［J］.Water Research，1984，18(11): 1443－1449.

［5］ BOCCELLI D L，TRYBY M E，UBER J G，et al.A reactive species model for chlorine decay and THM formation under rechlorination conditions［J］.Water Research，2003，37(11):2654－2666.

［6］ DUGAN N R，SUMMERS R S，MILTNER R J，et al.An alternative approach to predicting chlorine residual decay［C］//Proceedings of the Water Quality Technology Conference.New Orleans:American Water Works Association，1995:1317－1337.

［7］ KOECHLING M T.Assessment and Modeling of Chlorine Reactions with Natural Organic Matter:Impact of Source Water Quality and Reaction Conditions［D］.Cincinnati，Ohio:Department of Civil and Environmental Engineering，University of Cincinatti，1998.

［8］ CLARK R M，SIVAGANESAN M.Predicting chlorine residuals in drinking water:Second order model［J］.Journal of Water Resources Planning and Management，2002，128(2):152－161.

［9］ HALLAM N B，WEST J R，FORSTER C F，et al.The decay of chlorine associated with the pipe wall in water distribution systems［J］.Water Research，2002，36(14):3479－3488.

［10］ LEE G，TACHIKAWA Y，TAKARA K.Analysis of hydrologic model parameter characteristics using automatic global optimization method，annuals of disas［J］.Prev Res Inst，Kyoto Univ，2006，(49 B):67－81.

［11］ 李向阳，程春田，武新宇，等.水文模型模糊多目标SCE——UA参数优选方法研究［J］.中国工程科学，2007，9(3):52－57.

［12］ 郝媛，徐天东，孙立军，高速公路路面养护辅助决策系统［J］.计算机辅助工程，2007，16(3): 128－131.