基于逆变器死区的空间矢量脉宽调制仿真研究

王家军,郭 超,金利勤

(1.杭州电子科技大学自动化学院,浙江杭州310018;2.浙江浙能嘉华发电有限公司,浙江嘉兴314201)

0 引 言

近年来,随着磁性材料、半导体电功率器件以及控制理论的快速发展,永磁同步电动机驱动系统以其优良的结构特性在中小功率范围的运动控制中正扮演着越来越重要的角色[1]。空间矢量脉宽调制(Space Vector Pu lse Wid th Modulation,SVPWM)技术已经成为电压型逆变器的一个标准控制方法,并广泛应用于电动机的控制[2]。SVPWM实现时,为了防止直流母线的直通,常常在每个桥臂的上、下两个功率器件的触发信号之间增加一个死区时间[3]。目前已经有许多关于死区效应补偿的研究[4],本文没有通过Matlab/simulink仿真给出一种新颖的死区时间产生方法,然后给出一些由死区效应引起的零电流钳位的仿真结果。

1 空间矢量脉宽调制原理

如图1所示是三相电压型逆变器的结构图,图1中功率器件共有8种开关模式,相应的电压空间矢量可用Un(n=1,2,◦◦◦,8)表示。如图2所示,6个有效电压空间矢量(U1-U6)作为基本向量,构成含6个扇区的封闭六边形,另外两个空向量U7(000)和U8(111)用来填充调制周期中的空闲时间。在此向量空间中,任何电压向量都能被两个基本向量Un和U(n+1)合成。如图2中位于第一扇区的电压矢量US可以用U1(100)和U2(110)的合成矢量来表示,US为逆变器输出电压矢量。

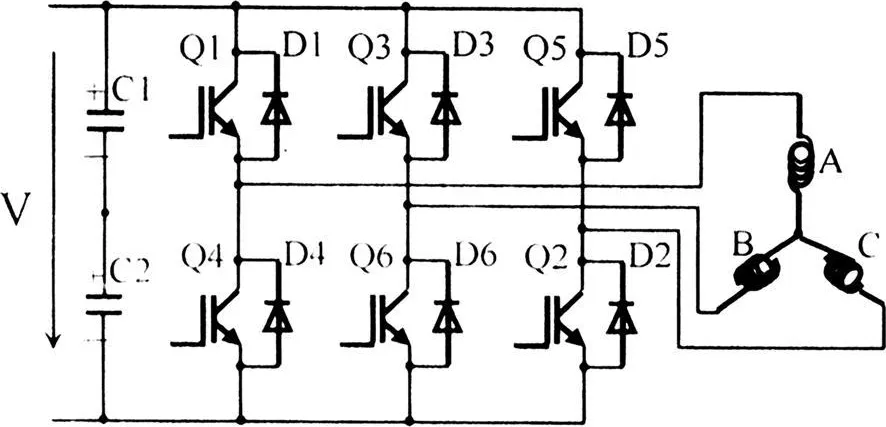
图1 三相电压型逆变器

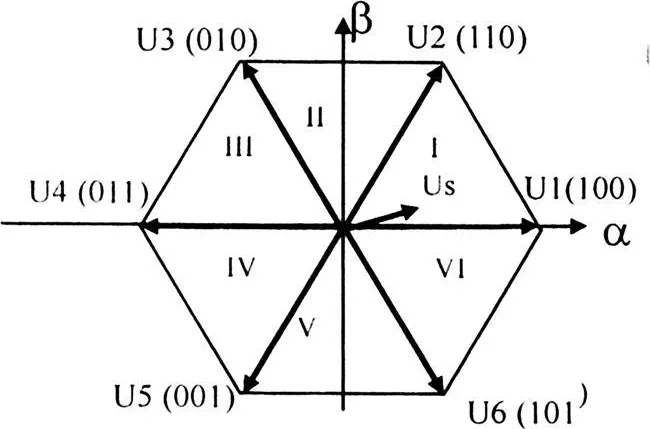
图2 空间矢量扇区图

在应用SVPWM技术时,首先,需要确定要合成的电压矢量US所在的扇区,计算出该扇区相邻两个基本电压空间矢量Un、U(n+1)的作用时间t1和t2。然后根据相邻电压矢量作用时间t1和t2,计算开关作用时间ta、tb和tc。最后,将开关作用时间和三角载波比较就得到SVPWM的输出时序。

(1)判断需要合成的电压矢量US的扇区。

US所在的扇区与两相固定坐标系(α-β)上的电压控制量Uα和Uβ有关。电压控制量Uα和Uβ与三相定子绕组轴abc上的相电压Ua、Ub和Uc之间的转换公式为:

对电压控制量Uα、Uβ作如下变换:

令Uref1＞0时,A=1,否则A=0;Uref2＞0时,B=1,否则B=0;Uref3＞0时,C=1,否则C=0。设N=A+2B+4C,则扇区与N的对应关系如表1所示。

表1 基于N的电压扇区测定

(2)计算X、Y、Z和电压空间矢量作用时间t1、t2。

X、Y、Z通过下面的公式计算:

式中,Ts是调制周期,Vdc是直流侧电压值。对于不同的扇区,矢量作用时间t1、t2与X、Y、Z的对应关系如表2所示。

(3)开关作用时间ta、tb、tc的计算。

开关作用时间可以通过taon、tbon和tcon的值来计算,taon、tbon和tcon的计算公式为:taon=(Ts-t1-t2)/4;tbon=taon+t1/2;tcon=tbon+t2/2。开关的作用时间ta、tb、tc和taon、tbon、tcon的对应关系如表3所示。将ta、tb和tc的计算结果与三角载波相比得到SVPWM信号的输出时序。

表3 各扇区的开关作用时间

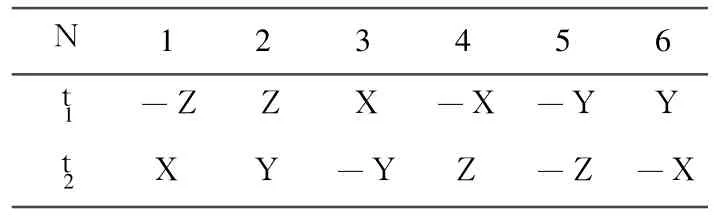
表2 t1和t2的测定

2 逆变器死区时间的生成方法

生成死区时间,首先必须考虑的一个问题是怎样把死区时间嵌入到SVPWM生成时序中。如图3所示给出了一种新颖的死区时间生成方法,图3中的传输延迟模块用来延迟低电平初始信号。高电平信号减去延迟信号的绝对值就是死区时间,该死区时间分别与初始高电平信号、延迟信号进行乘运算,从而嵌入到SVPWM生成时序信号中。

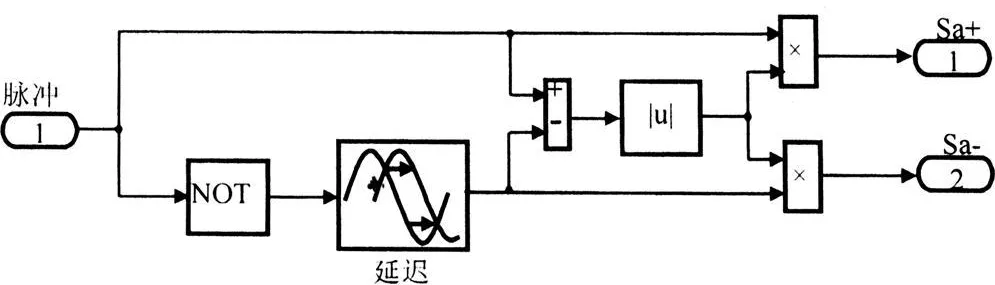
图3 逆变器死区时间的生成单元

3 系统设计仿真与分析

永磁同步电机控制系统的仿真模块如图4所示,包括一个速度PID控制器,两个电流PID控制器,dq/abc转换,SVPWM生成,IGBT电压型逆变器,永磁同步电动机模型和检测单元。速度环PID控制器的参数为P=0.045、I=12、D=0,电流环PID控制器参数为P=320、I=100、D=0,IGBT的道通时间是1μs,关断时间是2μs,dc直流电压是400V。在以下的2种仿真实验中,负载转矩为10N◦m。

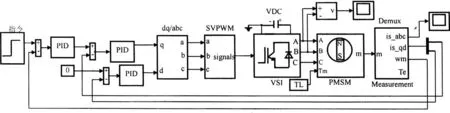
图4 永磁同步电机仿真结构图

(1)第一种情况仿真

死区时间设置为3μs,给定速度为300r/min,开关切换频率设置为10kHz,仿真结果如图5所示。这种带死区时间的永磁同步电动机仿真中,电动机转速跟踪给定速度的波动大约为0.9%,电磁转矩跟踪负载转矩的波动大约为4%。当电机电流过零点时,这种方案有零电流钳位时间。

(2)第二种情况仿真

死区时间为3μs,给定速度为60r/min,开关切换频率设置为10kHz,仿真结果如图6所示。从仿真结果中可以看出电机转速较低时,跟踪给定速度的波动变大,大约为12%,电磁转矩的波动也变大,大约为12%。从而得出当给定转速较低时,死区效应的影响将比高速时更明显的结论。

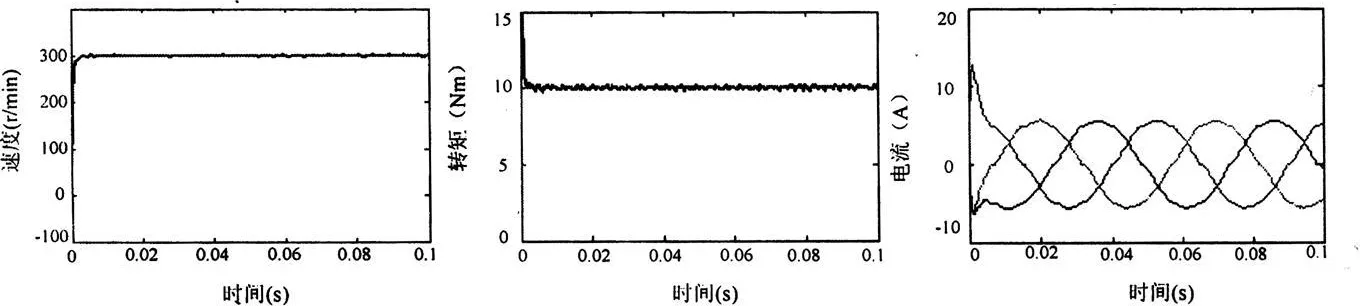
图5 第1种仿真结果

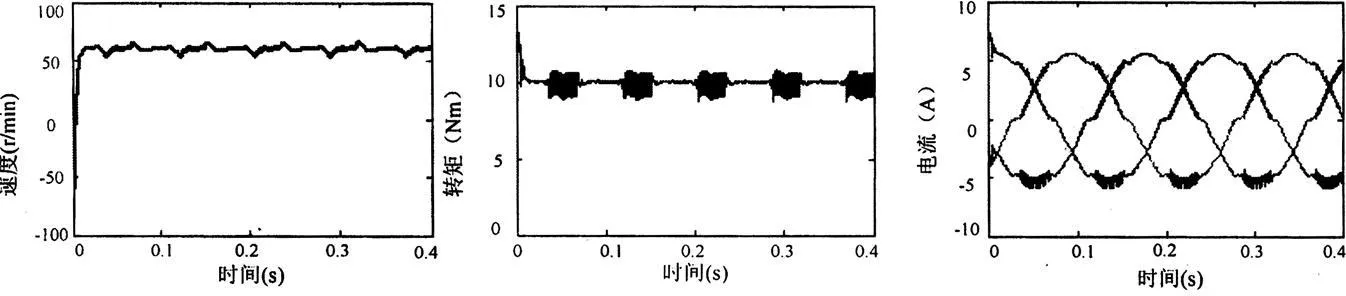
图6 第2种仿真结果

4 结束语

该文中给出了SVPWM的详细设计方案,并设计了一种新颖的生成死区时间的方法。该文在永磁同步电动机系统中利用带死区时间的电压型逆变器进行了两种SVPWM仿真,证明了逆变器死区时间生成方法的正确性和可行性。

[1] Kinnares V,Charum itC.Modu lating functions of space vector PWM for three-Leg VSI-fed unbalanced two-phase induction motors[J].IEEE Transactions on Power Electronics,2009,24(4):1 135-1 139.

[2] Gao Q,Asher GM,Sumner M,etal.Position estimation of AC machines over awide frequency rang based on space vector PWM excitation[J].IEEE Transactions on Industrial App lications,2007,43(4):1 001-1 011.

[3] Oliveria A C,Jacobina C B,Lima A M N.Improved dead-time compensation for sinusoidal PWM inverters operating at high switching frequencies[J].IEEE Transactions on Industrial Electronics,2007,54(4):2 295-2 304.

[4] UrasakiN,Senjyu T,Uezato K,etal.Adaptive dead-time compensation strategy for permanentmagnet synchronousmotor drive[J].IEEE Transactions on Energy Conversation,2007,22(2):271-280