基于协方差矩阵递推的故障诊断

胡玉成

(杭州电子科技大学信息与控制研究所,浙江杭州310018)

0 引言

随着现代工业技术的迅速发展,大型复杂系统中,设备不同部分的高度耦合,通常局部的故障除了直接体现出来以外,还会通过各个局部之间的连接传播到系统的其它部分,若不及时将故障诊断出来,将导致设备损坏,造成经济损失甚至重大人员伤亡。因此,及时诊断故障具有重大意义。目前基于数据驱动的异常监控已成为当前自动控制领域的研究热点[1,2]。文献3基于数据驱动的PCA故障诊断方法,需计算正常历史采样数据的协方差矩阵的特征值和特征向量,进行离线建模;建立模型后对在线数据进行检测,这样耗费大量的时间,不能做到快速实时的检测。针对PCA方法在故障诊断存在的不足,本文给出基于协方差矩阵递推的故障诊断方法。并通过仿真验证算法的有效性。

1 基于PCA的故障诊断

基于PCA的故障诊断方法,首先应用正常历史数据建立主元模型,然后通过检验新的观测数据相对于主元模型的背离程度系统是否发生了异常。一个多变量数据用如下矩阵Xn来表示:

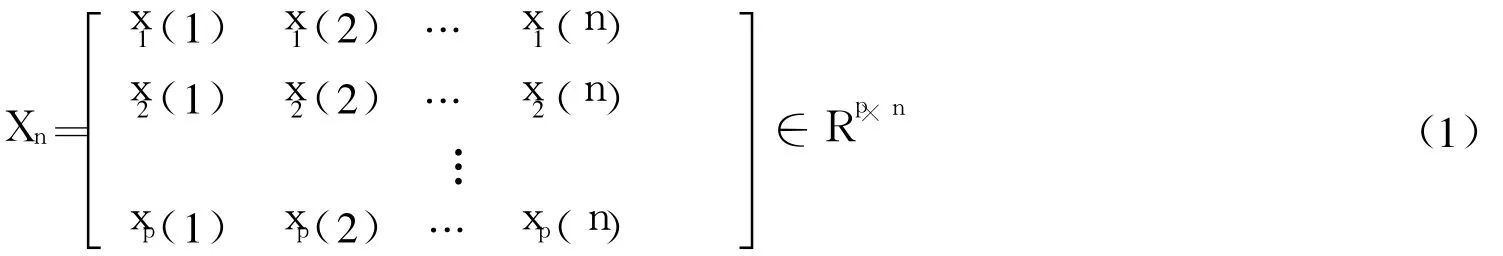
通过建立正常运行情况下的PCA模型[1,4-6],对在线观测数据进行故障诊断,常用Hotelling T2图和平方预测误差SPE(Squared Prediction Error)图监控。PCA通过离线建模和在线检测进行故障诊断,建立模型需要花费大量时间,且对于不同的设备要建立不同模型,这不能够做到实时检测。因此下面给出了协方差矩阵递推的方法。

2 协方差矩阵递推方法

2.1 协方差矩阵

协方差矩阵中各对角线上的元素反应的是各分量的方差,非对角线的元素反应的是各分量之间的协方差,协方差矩阵是对称矩阵[7]。式1记作前n个时刻的观测矩阵,当n+1个时刻到来时:

2.2 差分矩阵与标量值

每当有新的观测到来,就要及时更新协方差矩阵。通过实时跟踪协方差矩阵的差分矩阵,就可以实时判断系统中是否有异常存在。若差分矩阵变化充分大,表明有异常存在。定义差分矩阵:

令n+1时刻差分矩阵中所有元素绝对值和的均值为:

式中,M表示移动窗口,随着采样时间的增大而增加,⎿◦」表示向下取整。通常式9中要求至少有3个采样,γ1=0。判断系统在n时刻发生故障的条件是γn＞3σn。工业系统中,要实时快速的诊断出故障。协方差矩阵递推的故障诊断方法,对于不同设备不需要离线建模,能够实时的检测,它优于PCA。

式中,γn+1只关注差分矩阵的绝对值变化情况,它是跟踪整个系统变化的工具。

2.3 动态阈值

动态阈值的选取与γ同等重要,它可以是对一定窗口长度的γ值的平均值,即:

3 仿真实验

为了验证上述方法的有效性,给出一个仿真例子:汽车转动轴装配中所需要的电子管到电子管轭上的圆形定位焊接。自动定位焊接机器的输入必须控制在特定的操作内,这样机器才能产生好的焊接质量。为了控制这个过程,工程师需要测量4个关键变量,分别是:电压、电流、进给速度、气流。对系统进行采样,每个变量采样200个数据。若过程变量进给速度在180-200个时刻出现传感器故障,为异常采样数据[8]。

SPE统计量也称为Q统计量,它反应的是数据在残差子空间中偏离主元模型的程度,当SPE＞Qα时,则说明过程中出现了异常。在180-200个时刻是异常采样,大部分SPE＞Qα,说明有故障发生,但同时存在SPE＜Qα,属于漏检现象;在180个时刻之前的采样数据是正常的,但有部分残差(实线)超过控制限(虚线),属于误报的现象,如图1所示。

基于协方差矩阵递推的方法中,γn＞3σn则有异常发生。在180-200个时刻是异常采样,异常大部分都能够被检测出来,漏报率小;在180个时刻之前的采样数据的误检率相对PCA的较少;其误检率和漏检率比PCA都少,如图2所示。设备在运行的情况下,若漏报的数目较多,则存在较大的隐患,甚至引起重大事故;若系统中存在过多的误报现象,则会影响操作人员的工作。综合上述情况,基于协方差矩阵递推的方法优于PCA的方法。

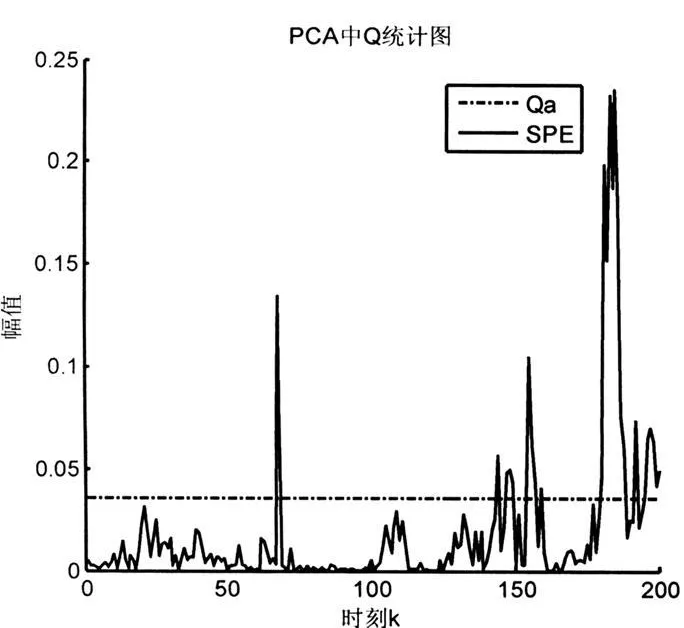
图1 PCA的SPE图

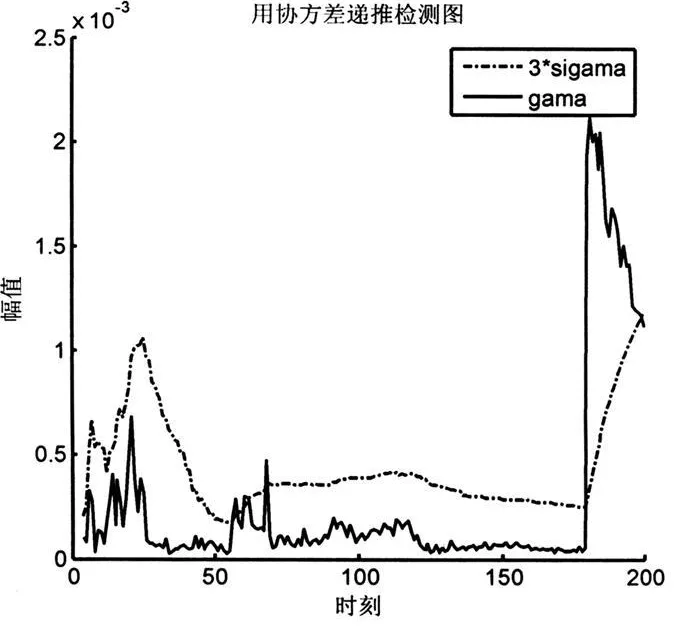
图2 协方差矩阵递推的检测图

4 结束语

本文给出了协方差矩阵递推方法,为了验证了协方差矩阵递推方法的有效性,通过仿真与传统的PCA故障诊断进行了对比。PCA需要通过正常的历史数据来离线建模,它需计算协方差矩阵及其特征值和特征向量;再在线检测。协方差矩阵递推方法提高了检测率,而且它只需要计算协方差矩阵,不需要建立模型,做到了实时动态检测。此外,协方差矩阵递推的方法存在的不足是:在故障诊断方面和PCA一样,都存在着模式复合作用。

[1] 周福娜.基于统计特征提取的多故障诊断方法及其应用研究[D].上海:上海海事大学,2009.杨帆,萧德云.大型复杂系统的动态SDG模型及传感器布置问题[J].控制理论与应用,2008,25(2):181-186.

[2] Carlos F Alcala.Reconstruction-based contribution for process monitoring[J].Automatica,2009,45(7):1 593-1 600.

[3] 胡静.相对主元分析理论及其应用研究[D].开封:河南大学,2005.

[4] 蒋浩天,拉塞尔E L,不拉茨R D.工业系统的故障检测与诊断[M].北京:机械工业出版社,2003:30-49.

[5] I.T.Jolliffe.Principal Component Analysis[M].Springer-Verlag,New York Berlin Heidelberg,2002:1-9.

[6] Heem in Yi Yang.Adavnced Prognosis and Health Management of Aircraft and Spacecraft Subsystems[D].Cambridge:Masschusetts Institute of Technology,2000.

[7] 范少荟,主元分析的若干扩展方法研究[D].开封:河南大学,2005.