基于线性双曲线模型的车道线检测算法

王晓云,王永忠

(杭州电子科技大学信息与控制研究所,浙江杭州310018)

0 引 言

智能驾驶辅助系统通常需要实现车道偏离预警、车辆横向控制和碰撞避免等功能[1]。其中基于视觉的车道线检测是实现上述功能的关键。在国内外研究中,现有的车道线检测方法大体分为基于特征的[2,3]和基于模型的车道检测算法[4-8]。但光照变化、阴影遮挡、噪声、道路边界或标志线不连续性等因素都会影响基于特征方法的检测效果。基于模型方法中常见的道路模型有直线,样条曲线[4],线性抛物线[5,6]等。本文提出一种新的基于线性双曲线模型的车道线检测算法。对经二维FIR滤波后的图像利用大津法实现车道边缘检测,可有效改善Canny边缘检测的不足,增加特征提取的准确性。区别于线性抛物线模型,本文对提取的车道边界点利用线性双曲线模型进行最小二乘拟合,可充分利用道路的边界信息,在车道线遮挡的情况下也能实现准确检测,提高了算法的鲁棒性。

1 线性双曲线车道模型

道路模型在车道线检测过程中具有重要作用。简单的道路模型计算量小,如直线模型,但缺乏描述不同形状道路的能力;复杂的道路模型灵活且适用于不同形状的道路,如B-Snake模型[4],但易受噪声和其他干扰因素的影响。

采用直线模型描述的道路可以表述为u=b(v-h)+e,其中(u,v)为图像上的道路边界点,h是道路消失点在图像中的v轴坐标值,b,e是直线模型的参数。一般而言,如图1所示,对于近处道路,AB,DC(v＞h+δ),直线模型通常可以准确地描述车道。但此时对于远端道路BE,CE(h＜v＜h+δ),直线模型将无法满足。

图1 线型双曲线模型

对于远端道路BE,CE可以近似为双曲线模型u=k/(v-h)+d,k,d是双曲线模型参数。为了准确表示图1中复杂的道路形状,可以将双曲线模型与直线模型组合起来,构成线性双曲线模型,其表达式为:

式中,k,b,c是线性双曲线模型的参数,f1(v)=k/(v-h),f2(v)=b(v-h)。对于远端道路BE,CE,即当v-h＜δ时,f2(v)bδ,且随v减小,f2(v)减小,而f1(v)增大。此时u主要由k/(v-h)项决定,符合远端道路为双曲线模型的假定。同理,对于近处道路AB,DC。当v-h＞δ时,f1(v)k/δ,且随v增大,f1(v)减小,而f2(v)增大,此时u主要由b(v-h)项决定,符合近处道路为直线模型的假定。

2 车道线检测

2.1 图像预处理

在对图像进行边缘检测之前,本文首先对图像进行预处理。利用道路的彩色信息分割边界增加了边界检测的难度同时会影响计算速度,为此将彩色图像转化为灰度图像。为了消除光照变化和噪声的影响,本文通过构建FIR滤波器算子对图像进行滤波平滑处理,实现图像特定区域的增强。

2.2 边缘检测

在对图像进行预处理后,为了获得车道边界,需要对图像进行边缘检测。常用的边缘检测算法有:Canny算子、Sobel算子、Robert算子等,但这些算子都存在一些缺点。因此,本文在对直路、左右转弯、阴影和车辆部分遮挡等典型道路图像进行二维FIR滤波的基础上,采用经典大津法[3,7],检测车道边缘,检测结果如图2所示。大津法的基本思想是选取的最佳阈值应当使得用该阈值二值化得到的两类间具有最好的分离性。

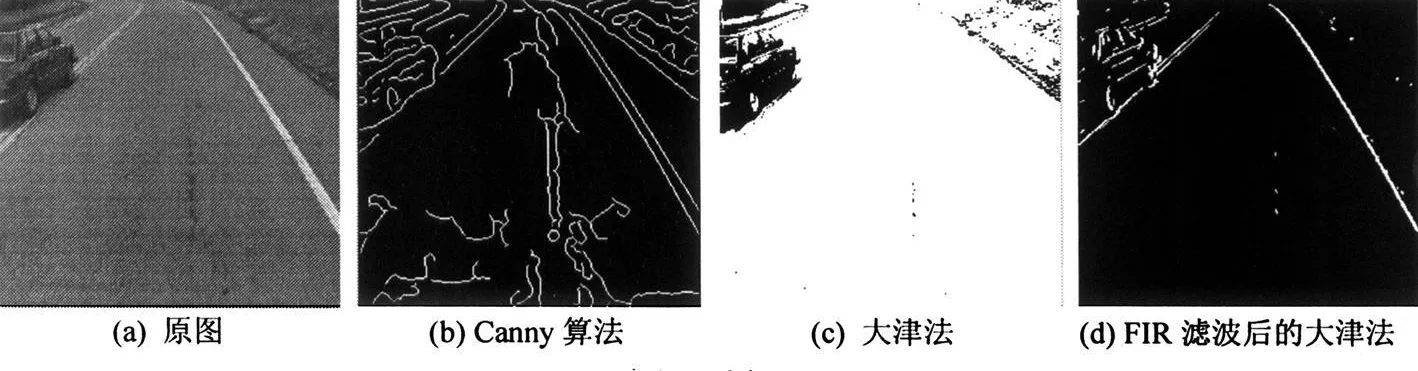
图2 车道线存在部分遮挡的二值化效果图

图2给出了不同道路状况下利用Canny算子和大津法以及本文所用方法进行边缘检测的实验结果。可以看出,当车道线存在部分遮挡时,Canny算子可以检测出道路边缘,但同时也检测出破损路面的边缘;直接利用大津法时,车道线或被高亮度区域淹没或车道线丢失,基本无法辨识;而经FIR滤波后再利用大津法则可以准确地实现边缘检测。

2.3 车道线提取

经过大津法阈值分割后,本文首先利用Hough变换初步获得道路的中线和消失点。Hough变换的直线参数方程可以表述为如下形式:

式中,ρ是直角坐标系的原点到直线L的距离,θ是ρ与x轴的夹角。θ的取值范围为-90°～+90°,

在实际应用过程中,可以拒绝那些不落在搜索区域内的直线。例如,在拍摄的视频图像中,水平线不可能是车道边界。因此本文先剔除Hough变换矩阵中θ值大于78°的象素值,将Hough变换搜索空间中每边的角度都限制在30°窗口内,并计算检测出的车道线的长度,当长度大于阈值,就认为其是车道线。由检测出的左右车道线的Hough变换参数,可以得到车道线在图像空间的投影消失点,进而得到线性双曲线模型中的参数h。

在获得消失点坐标后,本文采用Mid-to-Side[9]搜索方法得到车道左右侧车道线的内部边界点集L(l)和L(r)。将L(l)、L(r)和消失点坐标h代入线性双曲线模型中,利用最小二乘拟合法可计算出模型中的未知参数k,b,c,获得线性双曲线模型表示的车道线。

3 实验结果及分析

为验证本算法的有效性,本文利用卡内基梅隆大学的测试视频序列对本文提出的车道线检测算法进行了仿真实验。测试序列中每帧的图像大小都是240×256的RGB图。不同环境下利用本文算法和线性抛物线模型[5,6]进行车道标志线检测的实验结果如图3所示,其中第一行是本文方法的检测结果,第二行是线性抛物线模型的检测结果。从实验结果可以看出,本文算法对直线和曲线道路,存在阴影,光照变化和车道线被部分遮挡时都能实现很好的检测。文献5,6在拟合图3(b)、(c)、(d)中的弯曲道路时不够光滑,主要是因为进行线性模型和抛物线模型选择的分界点不具有自适应性。在图3(c)、(d)道路存在阴影和车道线被部分遮挡的情况下,利用线性抛物线模型拟合时,出现了明显的偏差,不能准确地检测出车道线。

图3 本文方法与文献5,6的实验结果比较

4 结束语

本文提出了一种新的基于线性双曲线模型的车道线检测算法,对经二维FIR滤波后的图像利用大津法实现车道的边缘检测,克服了直接采用大津法进行图像二值化或采用Canny等边缘检测算法在阴影、光照变化和车道线部分遮挡存在时,无法准确实现边缘检测的缺点。通过Hough变换初步获得车道的中心线及消失点的基础上,准确地提取车道的边界点,进而采用最小二乘拟合获得车道的线性双曲线模型。实验中选取直路和弯曲道路,以及有阴影和车辆遮挡的道路进行了测试,并与采用线性抛物线模型的方法进行了比较,结果验证了本文算法可以在有阴影、轻微遮挡及光照变化等情况下准确可靠地提取出道路的边界。

[1] McCall JC,TrivediM M.Video-based lane estimation and tracking for d river assistance:survey,system,and evaluation[J].Intelligent Transportation Systems,2006,7(1):20-37.

[2] Assidiq A A M,Khalifa O O,Islam M R,et al.Real time lane detection for autonomous vehicles[C].Kuala Lumpur:2008 International Con ference on Computer and Communication Engineering,2008:82-88.

[3] 管欣,贾鑫,高振海.基于道路图像对比度-区域均匀性图分析的自适应阈值算法[J].吉林大学学报,2008,38(4):758-763.

[4] Wang Y,Teoh E,Shen D.Lane detection and tracking using B-snake[J].Image and Vision Computing,2004,22(4):269-280.

[5] 郭磊,王建强,李克强.存在车辆干扰的车道线识别[J].汽车工程,2007,29(5):372-376.

[6] King H L.Lane Detection and Kalman-Based Linear-Parabolic Lane Tracking[C].Hangzhou Zhejiang:2009 International Conference on Intelligent Human-Machine Systems and Cybernetics,2009:351-354.

[7] 卢卫娜,史忠科.基于单目视觉的车道和道路边界同步检测[J].传感技术学报,2007,20(5):1 171-1 175.

[8] 刘富强,张姗姗,朱文红.一种基于视觉的车道线检测与跟踪算法[J].同济大学学报,2010,38(2):223-229.

[9] Chen Q,Wang H.A Real-Time Lane Detection Algorithm Based on a Hyperbola-PairModel[C].Tokyo:2006 IEEE Intelligent Vehicles Symposium,2006:1-6.