基于稀疏逼近的EEG信号的压缩感知重建研究

吴 敏 ，韦志辉，汤黎明，孙玉宝，肖 亮

1 南京军区南京总医院医学工程科，江苏， 南京，210002

2 南京理工大学 计算机科学与技术学院模式识别与智能系统实验室，江苏， 南京，210094

3 南京理工大学 理学院应用数学系，江苏，南京，210094

基于稀疏逼近的EEG信号的压缩感知重建研究

【作 者】吴 敏1，2，韦志辉2，3，汤黎明1，孙玉宝2，肖 亮2

1 南京军区南京总医院医学工程科，江苏， 南京，210002

2 南京理工大学 计算机科学与技术学院模式识别与智能系统实验室，江苏， 南京，210094

3 南京理工大学 理学院应用数学系，江苏，南京，210094

目的 对一维的多通道非平稳信号EEG随机非自适应地欠采样，高质量地重建原信号，从而实现EEG信号的自动检测与分析。方法 实验中以高斯函数及其一、二阶导数为原子的生成函数，构建了一个新的冗余多成份字典.随机高斯测量阵为测量矩阵，按压缩感知测量模型重建信号，并采用了稀疏逼近误差NMSE作为逼近程度的定量度量标准，判定实验结果。结果 所选字典中原子可更加有效地匹配EEG信号中的多种瞬时特征波形，从而能够对EEG信号形成更为稀疏的匹配追踪分解。基于压缩感知理论的信号采样只需使用不到原信号一半的样本数，即可高质量地重建原信号，对于重要的瞬时特征波形能够很好地保持。结论 基于压缩感知理论的信号采样包含了原信号的足够信息，利用EEG信号的稀疏性（或可压缩性）先验条件，通过一定的线性或非线性的解码模型可以以很高的概率重建原始图像或高维信号。

压缩感知；棘波检测；多成份字典；稀疏逼近误差；稀疏表示；匹配追踪

脑电图(Electroencephalogram-EEG)是一维的多通道非平稳(non-stationary)信号，反映了大脑的神经电生理活动，是癫痫等脑疾病临床诊断与治疗的主要依据。在医疗实践中，通常对EEG要进行长时间的多通道测量，而且为了克服噪声与误差的影响，需要对诱发电位进行多次测量。这样一来，产生了大量数据，需要占有很大的存储空间，对便携式脑电图仪提出了很高的硬件配置要求，制约了该类脑电图仪的推广应用。当前通常解决这一问题的方法是对采样后的EEG数据进行压缩处理，以节约存储空间。然而，这种先高速率采样再压缩的方式，极大地浪费了硬件资源。

1 压缩感知的测量重建模型

CS 理论指出：利用随机测量矩阵可把一个稀疏（或可压缩）的高维信号投影到低维（相对于高维）的空间上，并证明了这样的随机投影包含了重建信号的足够信息。利用信号的稀疏性（或可压缩性）先验条件，通过一定的线性或非线性的解码模型，可以以很高的概率重建原始图像或高维信号。CS理论为人们提供了一种图像或者信号的非常简洁的表达，即最优的稀疏表示（sparse representation)，如图1所示。CS理论在图像理解与建模、模式识别（如特征提取和维数约减）等领域有着非常重要的应用价值。压缩感知测量可用下式表示：

图1 压缩感知测量过程示意图[1]Fig.1 Measurement process of Compressive Sensing

式中字典Φ∈RN×L，Θ∈RM×N为测量矩阵，α∈RL为稀疏分解系数，大部分元素为零，只有很少的非零系数，为经随机投影后的测量数据，期望测量数据的维数应远小于原信号的维数[1]。利用分解系数α的稀疏性先验知识，在一定条件下，从测量数据y通过最优化模型可高概率重建原信号。同时，为了降低问题难度，将l0范数替换为l1范数，可将原问题凸化，，数学模型如下[2]：

该重建模型即为经典的基追踪问题。文献[1]、[2]指出，当θ为随机高斯测量阵时，对于K稀疏信号，如果测量样本数M≥cKlog(N/K)时，c为一个小的正常数，通过模型（2）可以以很高概率重建原信号，其中字典Φ的选择非常关键。

2 稀疏逼近多成份字典的选择

棘波是癫痫阵发性异常脑电波形的最基本形式，多为负相，有时为正相，有时还表现为双相、三相的结构，体现出了多样的形态结构特征[3](图2)。单一结构类型的原子并不能有效匹配棘波的多种形态结构，因此字典中应包含多种结构类型的原子。墨西哥帽小波是高斯函数的二阶导数，高斯小波是高斯函数的一阶导数，这两种小波在信号的多尺度奇异性检测与提取中具有重要的应用，很适合于检测分析非平稳EEG信号中的瞬时结构。高斯小波可有效匹配双相结构的棘波，而三相棘波可由墨西哥帽小波有效表示。同时，小尺度的高斯函数可有效匹配单相结构的棘波，大尺度的高斯函数则可有效表示信号中低频成份[4]。

图2 极性不同的各种单发棘波示意图Fig.2 Single EEG spike with various polarities

本文以高斯函数及其一、二阶导数为原子的生成函数，构建了一个新的冗余多成份字典。字典中原子可更加有效地匹配EEG信号中的多种瞬时特征波形，从而能够对EEG信号形成更为稀疏的匹配追踪分解。

3 EEG信号的压缩感知重建实验

实验中选用为上述多成份字典，测量矩阵采用随机高斯测量阵，按模型（2）重建信号[5]，采用稀疏逼近误差NMSE （normalised mean square error）作为逼近程度的定量度量标准。

图3-图6给出了针对两组EEG信号在不同测量样本数M下，压缩感知重建结果。在这些图中，实线为原EEG信号，原EEG信号维数N为800，虚线为经模型（2）压缩感知重建信号。

图3和图4给出了针对两组不同信号，随机投影样本数为380，重建NMSE分别为 0.0081和0.0019时，压缩感知重建信号与原EEG信号间的比较图形。可以看出，只需使用不到原信号一半的样本数，即可高质量地重建原信号，对于重要的瞬时特征波形能够很好地保持，有利于后续的信号处理。

图3 压缩感知重建结果，随机投影样本数为380，NMSE=0.0081Fig.3 Reconstruction results of compressive sensing ,the sample size for the random projection M as 380, NMSE = 0.0081

图4 压缩感知重建结果，随机投影样本数为380，NMSE=0.0019Fig.4 Reconstruction results of compressive sensing , the sample size for the random projection M as 380, NMSE = 0.0019

图5和图6给出了针对上述两组不同信号，随机投影样本数为200，重建NMSE分别为 0.0276和0.0236时，压缩感知重建信号与原EEG信号间的比较图形。可以看出，在只使用原信号的样本数时，仍可重建原信号的主要轮廓波形，对于重要的瞬时特征波形能够较好地保持。

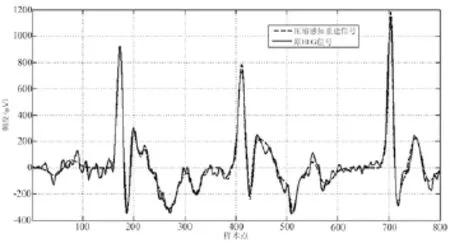
图5 压缩感知重建结果，随机投影样本数为200，NMSE=0.0276Fig.5 Reconstruction results of compressive sensing ,the sample size for the random projection M as 200, NMSE = 0.0276

图6 压缩感知重建结果，随机投影样本数为200，NMSE=0.0236Fig.6 Reconstruction results of compressive sensing, the sample size for the random projection M as 200, NMSE = 0.0236

4 不同字典下EEG信号稀疏表示结果与时频能量密度分析

基于压缩感知的数学模型（2），进一步将本文多成份字典与文献[6-8]中经典的Gabor字典的稀疏逼近性能进行比较。依据文献[6-8]的离散计划，Gabor字典中原子个数计算为O[N(log2N)2]。按照本节中各自由参数的采用计划，本文多成份字典中原子个数复杂度为O(Nlog2N)，与Gabor字典相比，本文字典中原子数较少， 降低了原子搜索复杂度。同时，应用文献[9]的快速算法，匹配追踪在本文字典下每一次迭代的复杂度的仅为O(Nlog2N)，有效地降低了匹配追踪算法的复杂度，提高了脑电信号的稀疏分解效率。

匹配追踪获取的M项稀疏逼近可用来估计信号的时频能量密度，即通过对原子φγi的Wigner-Ville分布求和得到。原子φγi的Wigner-Ville分布定义为[7]：

下面应用匹配追踪算法获取临床数字EEG信号在本文字典下的M项稀疏逼近。图7(a)给出了信号维数为840的(记录长度为3.5 s，数据采样率为240 Hz)具有三个分离棘波的EEG片段.由40个原子构成的稀疏逼近如图7(b)所示，尽管只使用很少的原子，仍然能够很好保持原EEG信号的结构，充分说明了本文原子能够有效匹配棘波结构。图7(c)给出了图7(a)的Wigner-Ville时频能量密度。图7(d)展示了在本文字典下应用(3)式计算的时频能量密度估计，在棘波处呈现出与背景不同的脊(ridge)结构能量模式，有利于对棘波的检测与识别。

图7 临床EEG信号片段的M项稀疏逼近及其时频能量密度估计(a)原EEG信号(b)M项稀疏逼近(c) Wigner-Ville时频能量 (d)时频能量密度估计 (c)(d)中灰度由暗到亮代表能量密度的由小到大Fig.7 The M-terms sparse approximation and time-frequency energy density of clinical EEG tracings.(a)original EEG signals; (b)M-terms sparse approximation; (c)Wigner-Ville time-frequency energy density; (d)the estimate of time-frequency energy density（In(c) and (d), the intensity of brightness corresponds to the intensity of time-frequency energy density）

下面进一步比较本文多成份字典与Gabor的匹配追踪稀疏逼近性能。采用稀疏逼近误差NMSE（normalised mean square error）作为逼近程度的定量度量标准，定义如下：

图8和图9给出了本文多成份字典与Gabor字典针对两组信号只使用前40原子的匹配追踪重建信号。图8中本文多成份字典的NMSE = 0.0073，Gabor字典的NMSE = 0.0219，图9中本文多成份字典的NMSE= 0.0206，Gabor字典的NMSE = 0.0459。从图形中可以看出，两个字典都能够较好重建原EEG信号，相比较而言，本文字典的稀疏逼近误差更小，能够生成更为稀疏的表示。

图8 本文字典与Gabor字典在相同原子数下匹配追踪重建信号的比较Fig.8 The comparison of the reconstructed signal based on matching pursuit between our dictionary and Gabor dictionary with the same number of atoms

图9 本文字典与Gabor字典在相同原子数下匹配追踪重建信号的比较Fig.9 The comparison of the reconstructed signal based on matching pursuit between our dictionary and Gabor dictionary with the same number of atoms

图10和图11分别给出了针对图8与图9中两组样本两字典下匹配追踪重建信号NMSE随原子数增加时的衰减图形。从图中可以看出，本文字典的NMSE衰减速度更快。由于本文字典中包含多种形态类型的原子，从而能够更加有效匹配EEG信号中多种瞬态波形结构，从而对EEG信号具有更强的稀疏逼近能力。

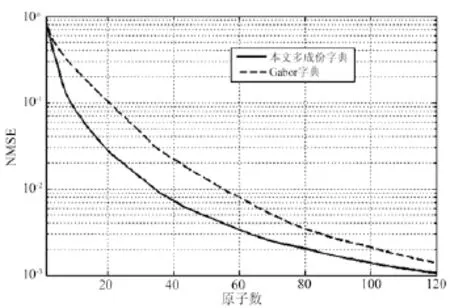
图10 针对图8中EEG信号，两字典的NMSE衰减图形Fig.10 In connection with EEG of Fig.8, the attenuation graphics of NMSE for two dictionaries

图11 针对图9中EEG信号，两字典的NMSE衰减图形Fig.11 In connection with EEG of Fig.9, the attenuation graphics of NMSE for two dictionaries

5 讨论

本研究针对一维的多通道非平稳信号EEG[10，11]，采用高斯函数及其一、二阶导数为原子的生成函数，构建了一个新的冗余多成份字典，随机高斯测量阵为测量矩阵，按压缩感知测量模型重建信号，采用了稀疏逼近误差NMSE作为逼近程度的定量度量标准。实验结果表明：所选字典中原子可更加有效地匹配EEG信号中的多种瞬时特征波形，从而能够对EEG信号形成更为稀疏的匹配追踪分解。

本文随机采样包含了原信号的足够信息，利用信号的稀疏性（或可压缩性）先验条件，通过一定的线性或非线性的解码模型，可以以很高的概率重建原始图像或高维信号。只需使用原信号一半的样本数，即可高质量地重建原信号，对于重要的瞬时特征波形能够很好地保持，有利于后续的数据处理。

[1] E. Cand`es, J. Romberg，and T. Tao. Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information[J]. IEEE Trans. Inform. Theory, 2006, 52(2): 489–509.

[2] D. Donoho. Compressed sensing[J]. IEEE Trans. Inform. Theory，2006, 52(4): 1289–1306.

[3] 吴立文主编. 临床脑电图图谱, 第一版. 北京:中国协和医科大学出版社, 2007.

[4] 吴敏, 韦志辉, 汤黎明，等．基于稀疏表示的两阶段脑电癫痫波检测算法研究[J]. 中国生物医学工程学报,2009, 28(4): 535-543.

[5] 吴敏, 韦志辉, 汤黎明, 等．一种基于稀疏表示模型的脑电图信号分析方法[J]．临床康复与医学工程．2008, 12（4）：667-670.

[6] M. L. Brown，W. J. Williams, and A. O. Hero. Nonorthogonal gabor representation of event-related potentials[A]. in Proceedings of the 15th Annual International Conference of IEEE Engineering in Medicine and Biology Society[C]，1993, 314–315.

[7] P. J. Durka and K. J. Blinowska. A unified timefrequency parametrization of EEGs[J]. IEEE Engineering in Medicine and Biology, 2001, 20(5): 47–53，

[8] S. Aviyente, E. Bernat, S. Malone，and W. Iacono. Analysis of event related potentials using pca and matching pursuit on the time-frequency plane[A]. IEEE International Conference of the Engineering in Medicine and Biology Society[C], 2006, 424–427.

[9] Stéphane Mallat，Zhifeng Zhang. Matching pursuit with timefrequency dictionaries [J].IEEE Trans on Signal Processing，1993，41(12):3397-3415.

[10] 刘铁兵, 汤黎明, 吴敏, 等．基于独立分量分析的癫痫脑电信号分析研究[J]．医学研究生学报, 2007，20(3): 278-280.

[11] Wu Min, Wei Zhihui, Tang Liming . et al. Research of virtual never induce electrical signal auto cheek technology[A]. 7th Asian Pacific Conference on Medical Biological Engineering APCMBE[C], 2008, Beijing, China

医疗器械生物学评价国际标准进展与2010年ISO/TC194年会

国际标准组织医疗器械生物学评价标委会（ISO/TC 194 ）第22届医疗器械生物学评价国际年会于2010年6月28日至7月2日在柏林召开。来自10多个国家的70多位医疗器械生物学评价的专家和监管部门代表出席了本次会议。中国医疗器械生物学评价技术委员会代表团一行共13人，包括中国医疗器械生物学评价秘书处（济南中心）4人、国家食品药品监督管理局医疗器械技术审评中心2人、北京审评中心2人、深圳审评中心2人、强生、雅培、微创公司各1人。本次会议共设9个工作组会议和1个主题研讨会。

工作组会议其中包括负责医疗器械体外细胞毒性试验的标准起草的第5工作组（TC 194/WG 5）、负责医疗器械遗传毒性、致癌性和生殖毒性试验的标准起草的第6工作组（TC 194/WG 6）、负责医疗器械刺激和致敏试验的标准起草的第8工作组（TC 194/WG 8）、负责医疗器械与血液相互作用方面的标准起草的第9工作组（TC 194/WG 9）、负责医疗器械植入试验的标准起草的第10工作组（TC 194/WG 10）、负责医疗器械可滤沥物的允许限量的标准起草的第11工作组（TC 194/WG 11）、负责ISO10993-18医疗器械材料表征和ISO10993-19材料理化、形态学、表面特性表征的标准起草的第14工作组（TC 194/WG 14）、负责医疗器械生物学评价策略性方法的标准起草的第15工作组（TC 194/ WG 15）。各组分别就医疗器械生物安全性评价、化学表征、风险评估管理策略等方面进行了广泛深入讨论。

在纳米材料医疗器械安全性评价的主题研讨会上，与会代表探讨了纳米材料的安全性与风险评估问题。其中包括：纳米材料的各种纷繁复杂的存在形式，如纳米涂层形式、有机纳米材料、无机纳米材料、溶解性及非溶解性纳米材料等，这些多样化的产品形式使得材料的表征和毒理学评价变得异常复杂和困难。需要表征的性能包括材料的化学组成、粒径及粒径分布、质量、表面积、聚集态、毒代动力学等。由于纳米粒子主要易于聚积于肝脏，特别是当直径＜20nm时，会会更广地分布在各种组织及细胞中，其代谢周期和代谢程度目前还不明确。另外，纳米粒子在人体中往往不是以单个粒子的形式存在，往往会吸附或与蛋白结合，因而纳米粒子产品的评价需要case by case。

主题研讨会上ISO/TC229的联络人Lang博士介绍了关于纳米技术的最新标准和OECD的有关文件，如将于2011年发布的ISO10801纳米银材料刺激试验、ISO10808纳米银材料吸入毒性试验。

通过参加本行业内的国际会议，尤其是作为中国生物学评价技术委员会秘书处成员参加大会，能够真正参与进工作组的讨论，并有机会对中国代表团的提案进行解释和辩护，既锻炼了能力，也提高了专业知识，同时也扩大了中国生物学评价技术委员会的国际影响，提高了我国生物学评价在国际行业内的地位。

（孙立魁 ，骆红宇）

The Reconstruction Study of EEG Signal Based on Sparse Approximation & Compressive Sensing

【Writers】Wu Min1,2, Wei Zhihui2,3, Tang Liming1, Sun Yubao2, Xiao Liang2

1 Nanjing General Hospital of Nanjing Area Command, Nanjing, Jiangsu, 210002, China
2 Lab of Pattern Recognition and Artificial Intelligence, Institute of computer science and technology, University of science and technology, Nanjing, Jiangsu, 210094, China
3 Department of Applied Mathematics, Institute of Science, University of science and technology, Nanjing 210094, China.

Objective Due to random sampling of non-adaptive, high-quality reconstruction of the original signal, one-dimensional non-stationary multi-channel EEG signal can be achieved automatic detection and analysis. Methods A new multicomponent redundant dictionaries with the atoms of the Gaussian function and its first and second derivatives was built in the paper, and reconstructed signal base on compressed sensing measurement model. Results The selected dictionary atoms can more effectively match the EEG signals in a variety of transient characteristics of the waveform, allowing the formation of EEG signal is more sparse matching pursuit decomposition. With the theory based on compressed sensing signal sampling, only half of the original signal with different sample size can be used to reconstruct the original signal quality, the important instantaneous features of the waveform can well be maintained. Conclusion Signal sampling based on the theory of compressed sensing contains enough information of the original signal, using the prior conditions of EEG signals (or compressibility) sparsity , high-dimensional signal and original image can be reconstructed through a certain decoding of linear or nonlinear model.

Compressive Sensing, spike-wave detection, multi-component dictionary, normalised mean square error, sparse representation, matching pursuit

R540.4+1

A

10.3969/j.isnn.1671-7104.2010.04.002

1671-7104(2010)04-0241-05

2010-04-19

韦志辉，Email:gswei@mail.njust.edu.cn

国家高技术研究发展（863）计划 (2007AA12E100)；国家自然科学基金资助项目 (60802039、60672074)；教育部高校博士点专项科研基金(20070288050，M200606018)；江苏省研究生创新基金。