Gamma过程退化失效可靠性分析

孙中泉，赵建印

（海军航空工程学院 a.科研部；b.兵器科学与技术系，山东 烟台 264001）

0 引言

可靠性是产品的一个重要的质量特性，它在满足用户“需求”方面起着极为重要的作用。传统的可靠性分析方法分析的对象为寿命数据，即产品的失效时间，通过对寿命数据的统计分析确定产品的寿命分布，进而确定产品的可靠性特征量。随着科技的不断进步，设计、制造方法以及使用材料的不断提高与改善，产品的可靠性越来越高，寿命越来越长，这使得产品在较短的时间内很难失效，由于得不到足够的失效数据，使得基于寿命数据统计分析的可靠性分析结果精度很差，理论与实际脱离，仅利用寿命数据评价产品可靠性变得非常困难。在某些情况下，如果产品的失效是由于其某些性能指标随时间不断退化而引起的，那么可以使用性能退化分析代替传统的失效数据分析来进行产品的可靠性评估。

实际上，相对于失效数据来说，产品的退化数据包含更多的可靠性信息[1]。另外，通过产品的退化信息进行可靠性分析更节省试验时间和费用。

所谓退化失效是指产品在以往的存储或工作过程中，产品的功能表征量随时间的延长而逐渐缓慢地下降，直至达到无法正常工作的状态（通常规定一个判定的临界值，即退化失效标准），产品退化过程一般是一个单调的过程。已经有一些学者对基于退化数据的可靠性分析方法进行了研究，文献[1]的工作对退化失效模型的一些问题做了讨论，而且在相当一般的条件下，提出了一些解决问题的方法；文献[2]的工作更进一步，采用多重多元回归模型来描述产品的退化过程，该模型包含了文献[1]所给出的模型；文献[3]利用退化信息对 ILF（Integrated Logic Family，一种新一代海底电缆的组件）进行了可靠性评估；文献[4]对一些相关的研究做了较好的总结。以上文献的研究主要利用随机系数或混合系数的回归模型来描述产品的退化量。但是，由于受到产品材料、应力以及环境的随机因素的影响，产品的退化过程一般可认为是一个随机过程，因此可以利用随机过程对产品退化失效进行建模。文献[5-6]采用布朗运动可用来描述产品退化量的增长，通过求解该过程首次达到失效阈值时间的分布来获取产品的失效分布。根据该随机过程，某一时间段内的退化量服从正态分布，不能保证退化量的增长是单调递增的。因此，对于描述单调变化的退化过程来说，该过程并不很合适。

对于退化量的描绘，Gamma过程是更为合适的，它能保证退化量是单调递增的。根据以上分析，为更好地描绘产品的退化失效，本文给出了一个基于随机Gamma过程的退化失效模型。

1 退化失效模型

设产品的性能参数为y (t)，它随使用时间的增加逐渐单调下降，产品初始性能值记为y0，它是一个已知量。另记 w(t)=y (t)−y0，表示到t时刻产品累积退化量的大小。由于退化量单调上升，对于任意的ti、tj，如果 tj＞ti，必有 w(tj)−w(ti)＞0。

Gamma分布为常用寿命分布之一，它具有形状参数和尺度参数两个参数，其形状参数取不同值时，Gamma分布形状多样，可表征多种数据变化特性。因此，这里我们利用Gamma分布来描述退化量的随机性，利用随机Gamma过程来描述退化量随时间变化的情况。即假设{w(t),t ≥ 0}为一个随机Gamma过程，它具有如下特性：

1）w(0)=0；

2）对任意的τ＞t，w(τ)−w(t)服从Gamma分布 Ga (α (τ)−α (t),λ(t))；

3）w(t)具有独立增量，即任意对于 t1＜t2＜…tn(n＞2)，诸增量 w(t2)−w(t1),…,w(tn)−w(tn−1)相互独立。

根据以上分析，退化量 w(t)服从Gamma分布Ga (α (t),λ(t))，其密度函数为

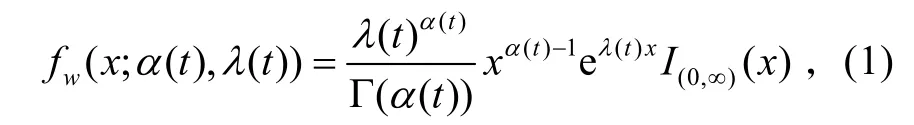
使用Gamma过程描述产品退化时，假设Gamma分布中的尺度参数λ (t)不随时间变化，即λ(t)≡ λ，而形状参数为时变参数。经验表明，一般情况下t时刻退化量的期望与时间的幂成正比，故设α (t)=ktb。因此，t时刻退化量 w(t)的分布密度为

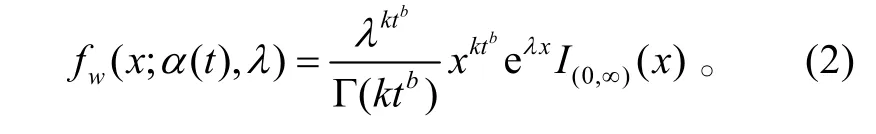
记产品的失效阈值为l，产品失效时间为T，根据退化失效的定义，则

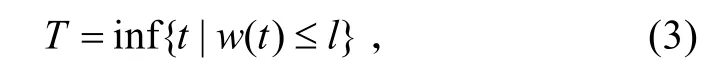
即失效时间为性能退化量首次达到失效阈值的时刻。也就是

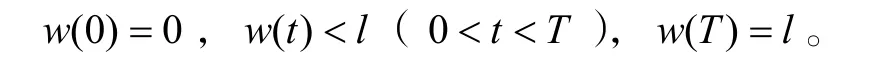
该Gamma过程首达时的分布即为产品的失效分布。一般情况下很难利用解析方法求得Gamma过程首达时分布，因而可考虑采用仿真的方法求解。这里我们利用Monte-Carlo仿真模拟退化量的增长过程来求产品的失效时间，由仿真产生的一组失效数据进一步可求产品失效分布的经验函数，并基于此进行可靠性统计推断。可按如下步骤仿真产生一个失效时间：

1）积退化量w=0，t=0；

2）产生服从Gamma分布函数Ga(α (t)−α (t−1),λ)的随机数wt，该随机数即为t时刻单位时间内的产品退化量的大小，令 w=w+wt；

3）累积退化量w与失效阈值l的大小，如果w ≥ l，则执行4），否则返回2）；

4）T为品的失效时间。

2 参数估计

设有m个样品做性能退化试验，分别在t1＜t2＜…＜tn时刻对样品进行测量并记录其性能退化量的大小，通过退化试验可得到数据{wij;i=1,2,…,m,j=1,2,…,n}，其中 wij表示第i个样品的第j次测量时测得的累积退化量的值。模型(2)中未知参数为λ、k、b，下面我们利用试验数据来估计它们。

产品t时刻的退化量大小 w(t)服从Gamma分布，分布的尺度参数不随时间变化，形状参数是时变参数，t时刻的退化量的均值和方差分别为

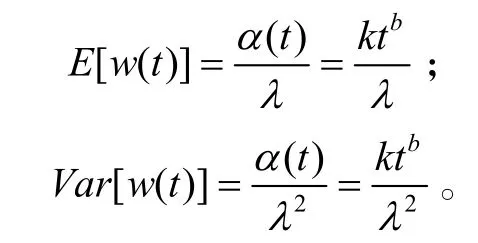
对固定j，j=1,2,…,n，由数据{wij;i=1,2,…,m}可求得第j次测量时刻产品退化量均值和方差的估计值由于则利用可求得λ的估计值

对上式两边取对数，有

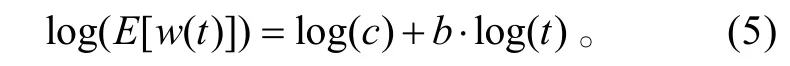
基于模型通过Monte-Carlo仿真即可获得产品的失效分布。

3 实例分析

金属化膜脉冲电容器是一种高可靠性器件，许多的激光惯性约束核聚变（ICF）试验装置，例如国外的NIF、OMEGA 或国内的神光III 等强激光装置[7-8]，均采用是该种电容器来提供泵浦能量。该型电容器元件是由两张单面蒸涂厚约20～100 nm的薄金属（铝或铝合金）的有机膜绕卷而成的，电流的引出是由元件两端面喷以金属层来实现的，由于膜在生产过程中不可避免地存在带有杂质或缺陷的区域，从而使得这些区域的耐电强度较低，形成“电弱点”。在外施电压不断作用下，电弱点处薄膜会首先被击穿而形成放电通道，当薄膜被击穿的同时，电荷通过击穿点形成大电流，引起局部高温，击穿点处的薄金属层会迅速蒸发并向外扩散使绝缘恢复，这样，局部击穿不会影响到整个电容器，电容器仍然可以使用，这一过程称为“自愈”[9]，单次自愈过程所造成的仅是电容量极微小的损失。在使用过程中电容器不断发生自愈，电容不断降低，当电容下降量超过预定阈值时电容器将发生退化型失效。对于工作在高场强下的金属化膜电容器来说，一般退化型失效模式的失效阈值取为5%[10]。

利用以上模型，我们下面对强激光装置所用的某型金属化膜脉冲电容器进行可靠性分析。共有8台电容器进行性能退化试验，电容器每充放电1 000次做一次测量，共运行了10 000次。

图1给出了电容器的容值退化量随时间的变化情况，图中横坐标为充放电次数，纵坐标为电容器容值。

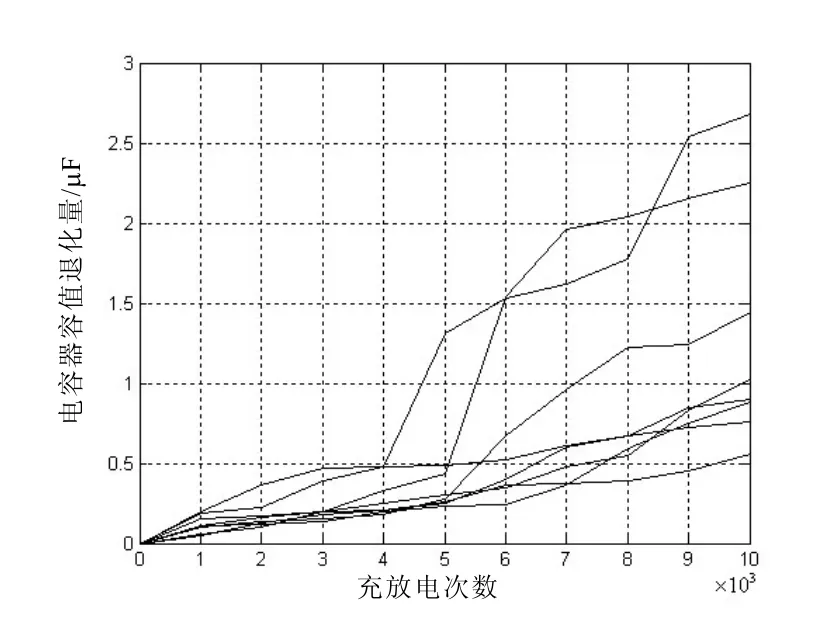
图1 电容器容值退化情况

将以上各估计值带入到式(2)即可获得退化量的分布密度函数，基于该函数，利用仿真方法获取退化量到失效阈值的一组首达时，即失效时间，利用这一组失效时间可进一步求得电容器失效分布的经验函数。

另外，由于经验函数在工程上不好应用，而双参数的Weibull分布可以表示故障率递增、递减或恒定的故障类型，具有很好的灵活性，因而可以用双参数的Weibull分布拟合该经验函数，双参数的Weibull分布函数及其密度函数为

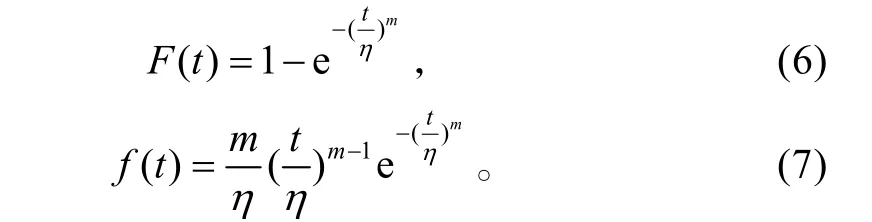
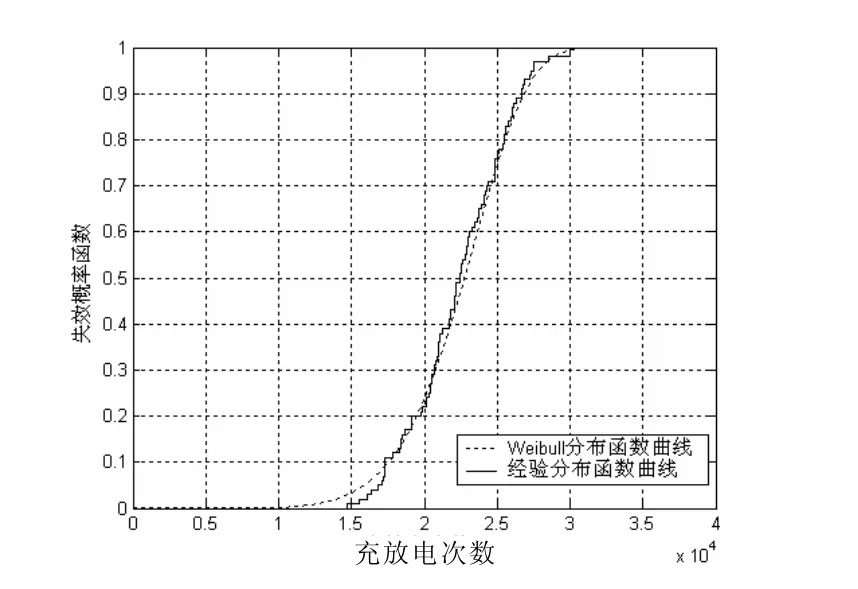
图2 电容器失效概率曲线

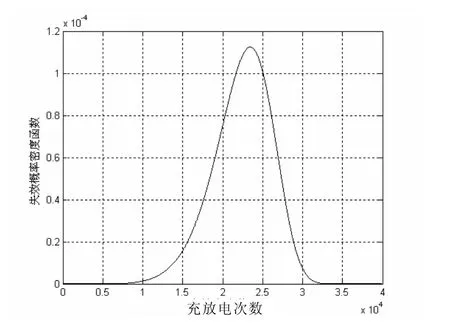
图3 Weibull 失效分布概率密度曲线

4 小结

由于受到其内部结构、材料特性、应力以及工作环境等因素的随机影响，产品的退化一般可认为是一个随机过程，并且该退化过程一般是单调变化的，当退化量首次达到其失效阈值时产品便会发生退化失效。根据退化过程的特点，本文给出了一个基于随机Gamma过程的退化失效模型，以及模型参数的估计方法，由于采用解析方法求解退化量首达时的分布存在一定难度，因而本文给出了一个基于仿真的求解方法。文章最后利用所得模型对强激光装置所用某型金属化膜脉冲电容器进行了可靠性分析并给出了可靠性评估结果，该结果表明所给模型在工程中是适用的。

[1]LU C J,MEEKER WQ.Using degradation measures to estimate a time-to-failure distribution[J].Technometrics,1993,35(2)∶161-174.

[2]CRK V.Reliability assessment from degradation data[C]//Proceedings Annual Reliability and Maintainability Symposium.2000∶155-161.

[3]CAREY M B,KOENIG R H.Reliability assessment based on accelerated degradation∶a case study[J].IEEE Trans.On Rel,1991,40(5)∶499-506.

[4]MEEKER W Q,ESCOBAR L A.Statistical Methods for Reliability Data [M].John Wiley &Sons,1998.

[5]SESHADRI V.The Inverse Gaussian Distribution[M].NY∶Springer,1999.

[6]WHITMORE G A,SCHENKELBERG F.Modelling accelerated degradation data using wiener diffusion with a time scale transformation[J].Lifetime Data Analysis,1997∶27-43.

[7]ENNIS J B,et al.Self-healing pulse capacitors for the national ignition facility(NIF)[C]//Proceeding of 12th IEEE International Pulsed Power Conference.Monterey,USA,1999∶118.

[8]周丕章,郭良福,陈德怀,等.激光聚变主放大器能源系统述评[J].强激光与粒子束,2003,15(4)∶346-351.

[9]代新,林福昌,李劲,等.高场强下金属化膜脉冲电容器失效的原因[J].高电压技术,2000,26(5)∶27-29.

[10]孙权,钟征,周经伦,等.自愈式金属化膜脉冲电容器耗损失效模型[J].强激光与粒子束,2004,16(8)∶1000-1004.