一种可靠性增长试验抽样数Max-Min准则的反馈修正方法
2010-03-24王星博李本威陈定海
王星博,李本威,陈定海,浦 鹏
(1.海军航空工程学院 a.飞行器工程系,山东 烟台 264001;b.青岛分院,山东 青岛 266041;2.91423 部队,辽宁 大连 116000)
成败型航空产品可靠性增长试验抽样数的研究是可靠性增长试验规划的一个重要方面。1992年,美国国防部科学顾问Seglie E.A教授在一篇武器系统研究报告中首次提出成败型产品的可靠性增长试验问题[1]。此后,这一问题引起许多学者的关注,纷纷开始进行相关研究。1996年Mu-Yeh Huang提出了MYOPIC可靠性增长试验规划模型[2-3]。受他的启发,其他学者发展了不同的序惯决策模型。1997年和2003年Gaver D.P.教授以导弹研制试验为例,从消除产品失效模式角度提出和发展了一种Max-Min模型,并建立Bayes分析方法,得到产品研制试验的最佳试验量[4]。
国内对这一问题研究较少。国防科大刘飞等针对固体火箭发动机开展了成败型产品可靠性增长试验规划研究,引入了Max-Min模型,取得了良好效果[5]。
本文从航空发动机部件系统性缺陷数角度结合试验数据的分析处理建立数学模型,在初始故障数分别服从二项分布、泊松分布、几何分布的条件下,通过理论推导给出带样本最大似然估计值反馈循环修正的可靠性增长试验数最小化最大准则,为成败型部件可靠性增长试验抽样数的确定提供了一种工程实用方法。
1 数学模型
对成败型航空发动机部件,作以下模型描述:产品总数为n;初始系统性缺陷数为F0;其导致的失效率均为p0;通过可靠性增长试验发现这些缺陷。若试验失败,则查找导致失败的故障模式,改进设计,尽可能地在以后的产品中消除此类故障。研究的问题为如何合理的选择试验抽样数t,使余下的(n − t)个产品成功数期望值最大[6]。
2 初始最小化最大停止准则
若原始设计生产n个产品,不做可靠性增长试验,此时该批产品的成功数 R0服从成功率为的二项分布,即则条件期望为
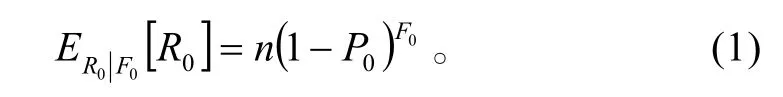
如果随机抽取t个产品样本进行可靠性增长试验,其中一些失效,通过确定故障模式和设计改进,从剩余产品中消除部分上述故障模式,使导致失败的系统性缺陷数变为tF。此时,剩余产品成功数期望为
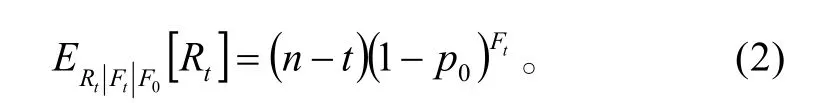
任一次抽样试验中,各种故障模式可能出现,也可能不出现,其出现概率为p0,假设出现了某种故障模式,通过改进设计成功消除的概率为b,则t次试验后任一故障模式仍然存在的概率为(1 − bp0)t,则 Ft关于 F0的条件分布为二项分布

由条件概率的性质可得t次试验后剩余产品成功数的期望值为
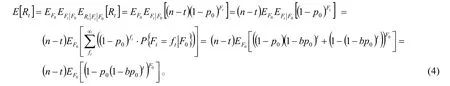
因此,只要知道 F0的分布特征(函数),就可求得 E[Rt]。
取初始系统性缺陷数 F0的分布律为P{F0},若所有参数已知或可估计,则由式(4)可得到最佳试验量 t0=t0opt(n),使剩余产品成功数期望值最大。实际应用过程中,初始参数 p0值不易确定,为消除E [Rt]与 p0的相关性,令 dE [Rt]dp0=0,求出 p0,使 E [Rt]取得最小值 Emin[Rt]。然后,基于可靠性增长的原则应选取使 Emin[Rt]最大的试验量,记为t0,这就是Max-Min准则。
本文在初始系统性缺陷数 F0符合不同的离散分布时,推导出了Max-Min准则的表达式,如表1所示(推导过程略)。

表1 0F 不同分布条件下的最小化最大准则表达式
3 逐次抽样样本估计值反馈修正方法
F0为部件初始系统性缺陷数,为离散分布的正整数,Ft也是如此,但目标值 E [Rt]却不一定是整数,它只是剩余产品成功数期望大小的度量。同样,我们也可将 F0定义为连续的随机变量来衡量系统性缺陷的多少。实际上,航空发动机部件结构的复杂性使系统性缺陷多样化,有的缺陷用整数来度量往往无法准确界定,用实数描述更为合理。
若初始系统性缺陷数 F0的概率密度为f0(x),x≥0,其含有的参数为θ1、θ2、…、θk(k ∈ N)。此时,Emin[Rt]值只与n、θ1、θ2、…、θk(k∈ N)和t 有关,消除了 p0对初始试验量选择的影响。
初始参数 θ1、θ2、…、θk(k ∈ N)可由专家信息和相似系统试验出现的系统性故障数目统计得到,记为此时,我们可以按照初步求得的t0为实验量进行抽样试验。
对每一个产品的测试,只有成败两种结果,将其作为同分布的随机变量Xi(i=1,2,…,t0),定义:
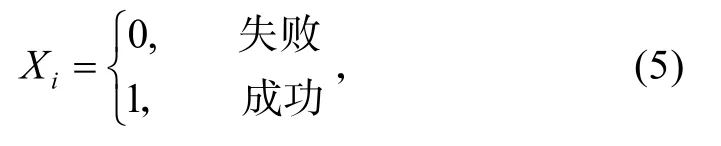
则可得:

式中:E[F0]为初始系统性缺陷数的数学期望,为θ1、θ2、…、θk的函数。
构造似然函数
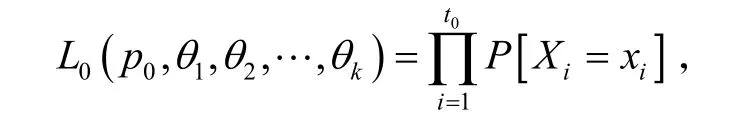
或对数似然函数
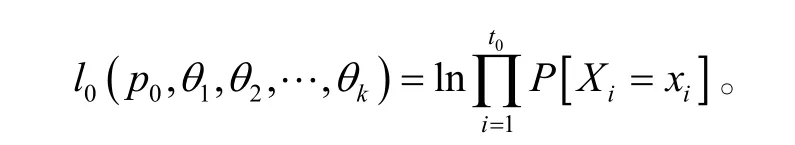
分别令
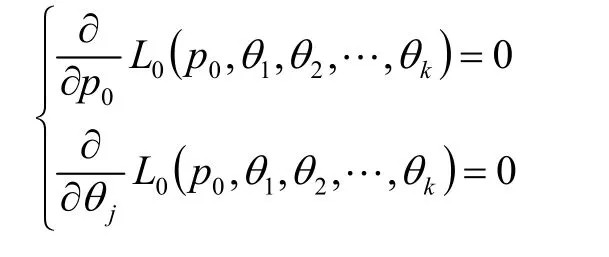
或者
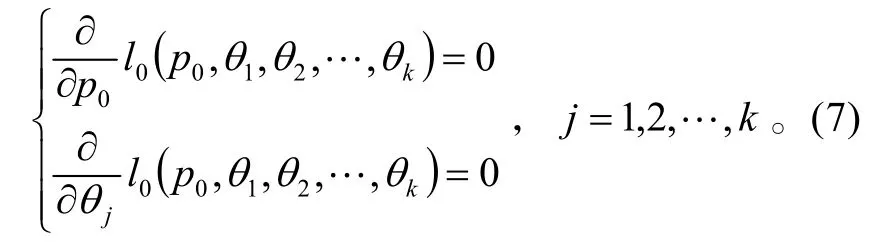
解上述由k +1个方程组成的方程组,即可得到各参数 θj(j=1,2,…,k)及 p0的最大似然估计值(对结构复杂的似然函数可由不同数值计算法由计算机求得极大似然估计)。由初步试验数据得的估计参数显然比先验参数及 p0更加可靠,因此,用这些估计参数代替原来的先验参数。
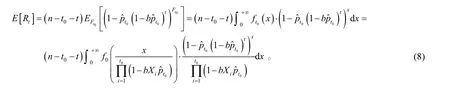
采用Max-Min准则求得使 E [Rt]值最大的t值,记为t1。如 t1=0,则停止试验,最佳抽样数取值为t0;如 t1≥ 1,说明前述的抽样不够,应追加试验。
接下来规划可靠性增长试验时,为保证最高效的抽样数量,采用的方式是每做一次抽样试验,充分利用样本信息进行初始值的反馈修正,最大程度上确保可靠性增长的目标。
再次抽样试验的结果记为Xt0+1,与上次抽样结果一起构造新的似然函数,由式(5)~(7)求得新的参数估计值此时,剩余产品系统性缺陷数为
剩余部件产品数量为n −(t0+1)。
成功数期望
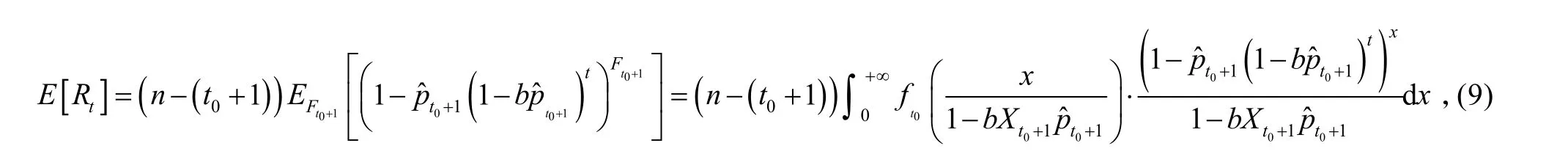
再次求使 E [Rt]最大的t值,记为t2。
重复上述步骤,直到 tM+1=0,停止试验。
则总共进行了 M + t0次抽样试验,这就是我们寻找的最佳试验量,最终剩余产品数为n− (M + t0),系统性缺陷数为:
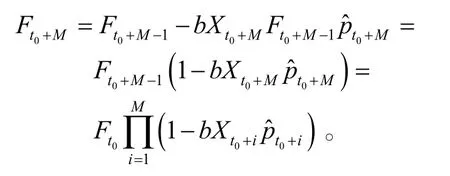
剩余部件产品成功数期望值为

4 实例分析
研制生产的某航空发动机部件数n=100个,随机抽取部分样品用于可靠性增长试验,初始系统性缺陷数服从区间在(0,m)上的均匀分布,由历史数据和专家信息初步确定先验分布参数m=10,期望
由式(4)得
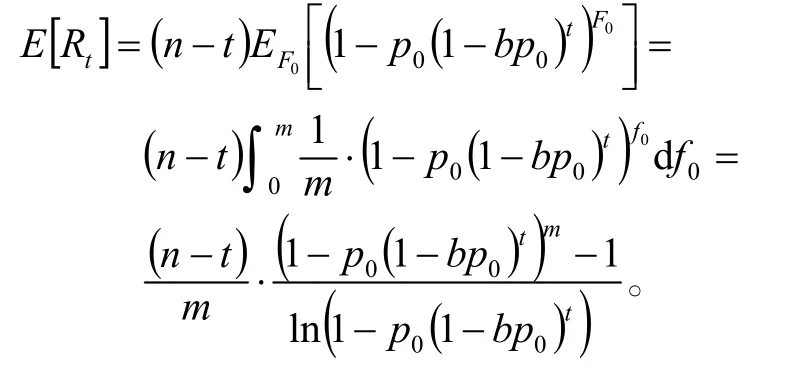
将上述参数代入计算,得
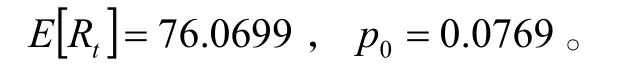
按 t0=12抽样,试验结果如表2所示:

表2 t0=12时可靠性增长试验结果
由式(6)、(7)构造最大似然函数,解得各参数的极大似然估计值。由式(8)解得 t1=4,应继续逐次抽样试验,将试验结果构造新的似然函数,进行新的参数估计。按本文的反馈修正方法进行试验和计算,结果如表3所示。

表3 可靠性增长试验结果
根据计算,不进行增长试验,该批产品的系统性故障模式数期望为5,由式(4)可求得产品总体可靠度期望为71.44%;按照Max-Min准则进行可靠性增长试验,抽样数为12,剩余系统性故障模式数期望为3.003 5,由式(8)可求得剩余产品可靠度期望为86.44%。由表3可见,经过试验的产品可靠性得到较大程度的提高。采用本文所提出的抽样反馈修正方法进行可靠性增长试验,抽样共分三阶段,抽样数分别为12、1、1,总数为14,剩余产品数为86,由式(10)可求得系统性故障模式数期望为2.631 9,剩余产品成功数期望为72.643 7,可靠度期望为84.47%。可见,通过试验的追加,故障模式数进一步减少,但剩余产品可靠度期望也有所降低,这并不能说明随着试验的进行,可靠性呈现负增长,而是因为此前的参数存在偏差,导致对产品的期望过于乐观。采用本文的分阶段抽样反馈修正方法更加可信和稳健。
5 结语
本文对航空发动机部件可靠性增长试验量的确定问题进行了初步研究。以剩余产品成功数期望值最大为目标函数推导了几种典型离散故障数分布情况下的Max-Min准则,首次提出一种反馈修正方法,得到最佳试验量;采用上述方法对某发动机部件进行了可靠性增长试验,效果明显。由于模型假设针对部件产品的总体,不涉及其复杂的内部构造和子系统,因此,该方法具有较强的适应性,在工程中也可用于各种成败型或现场不可修产品可靠性增长试验量的确定问题。
但是,如果试验前对产品性能水平无法把握,缺乏合理的先验信息时,采用不同的分布类型及参数初始值,对过程中参数估值的影响和由此产生的偏差问题不容忽视,尤其是抽样数过少时,较少的样本信息可能无法修正较大的先验值偏差,这些问题还有待进一步研究。
[1]SEGLIE E.How much testing is enough[R]//Paper Presented at the “Workshop on Statistical Issues in Defense Analysis and Testing” Sponsored by the National Research Council.Washington,D.C.,1992.
[2]HUANG MU-YEH,Douglas McBeth,Stephen B.Vardeman.Development test results[J].IEEE Transactions on Reliability,1995,3(45):189-198.
[3]HUANG MU-YEH.Design of developmental test programs for one-shot systems with two state reliability[D].Lowa State University,1995.
[4]GAVER D P,JACOBS P A.Probability models for sequential-stage system reliability growth via failure mode removal[J].International Journal of Reliability,Quality and Safety Engineering,2003,10(1):15-40.
[5]刘飞.固体火箭发动机可靠性增长试验理论及应用研究[D].长沙:国防科技大学,2006.
[6]刘飞,窦毅芳,张为华,等.固体火箭发动机可靠性增长试验规划初步研究[J].战术导弹技术,2007(6):1-3.
