局部对称共形平坦Lorentz流形中2-调和类空超曲面

汪兴上

(安徽师范大学数学计算机科学学院，安徽芜湖241000)

本文研究了局部对称共形平坦Lorentz流形中2-调和类空超曲面，得到

定理1 设Mn是局部对称共形平坦Lorentz流形中2-调和紧致类空超曲面，且具有常平均曲率，以S代表其第二基本形式模长的平方，K表示的数量曲率的Ricci曲率满足r≤εAKAA≤R，则成立如下的积分不等式

其中H为Mn的平均曲率。

1 准备工作

本文约定各类指标的取值范围如下

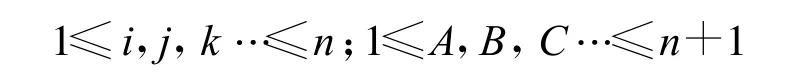
{ωA}为联络1-形式，将这些形式限制在Mn上，有

其中Rijkl表示Mn的曲率张量R的分量，hij为其第二基本形式h的分量，其共变导数hijk，hijkl定义如下:

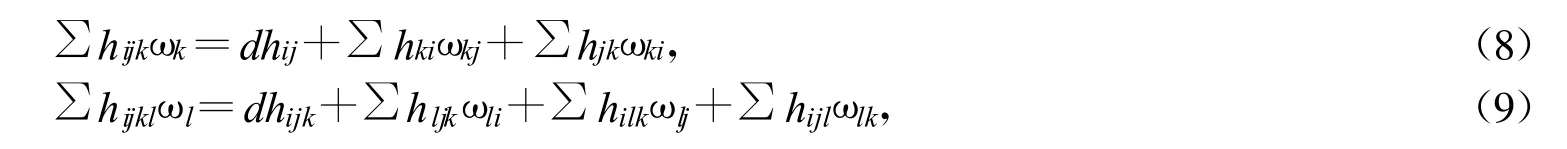
则Codazzi方程和Ricci恒等式分别为

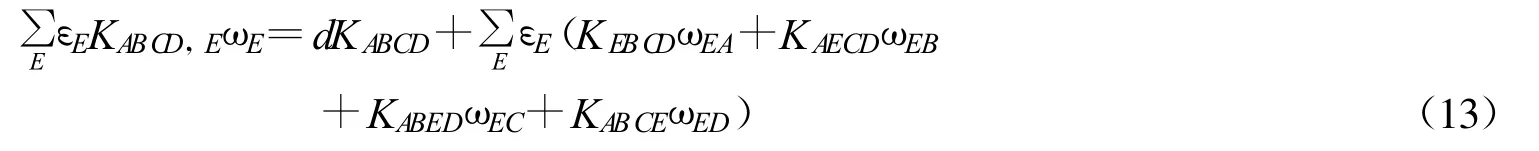
其中:εi=1，εn+1=-1。

限制在Mn上有

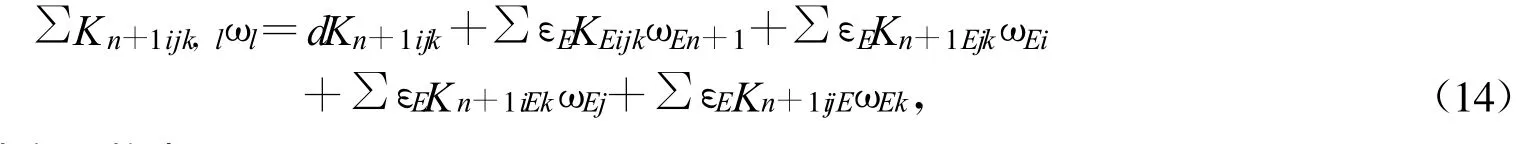
又Mn上Kn+1ijk的共变导数为Kn+1ijkl，即

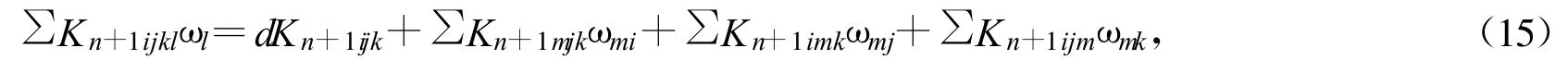
从而

引理1[4]Mn是中2-调和类空超曲面，则

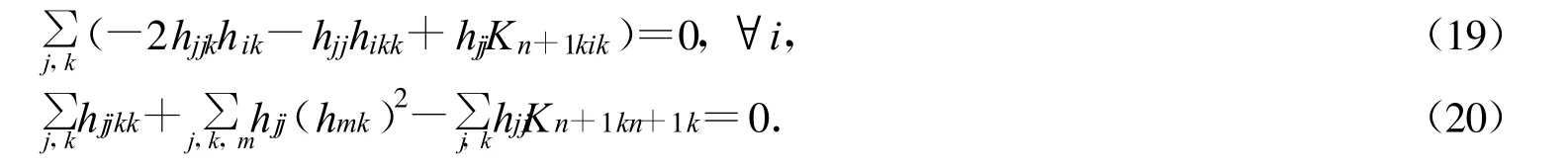
2 定理1的证明

由(10)和(11)得

利用(16)经简单计算，得

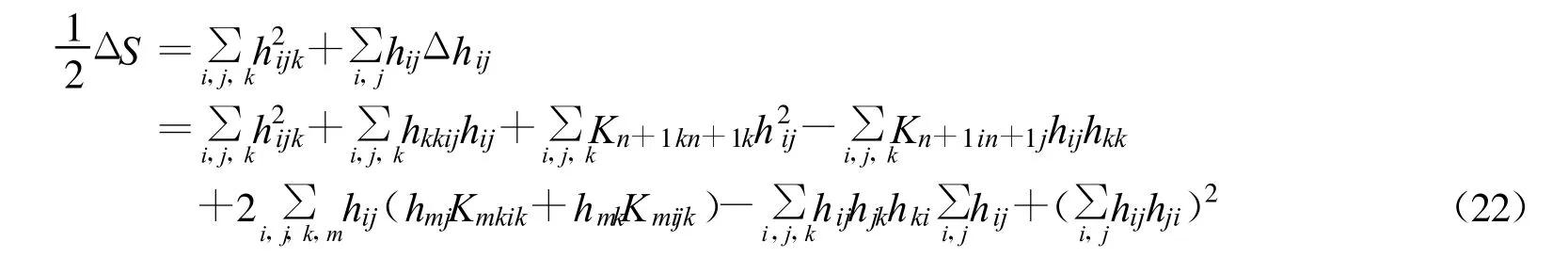
下面估计(22)式中的各项，由(17)得

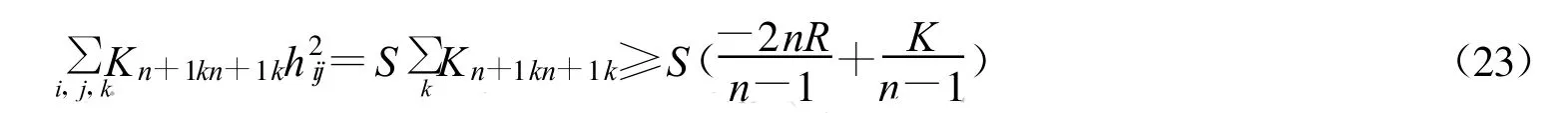
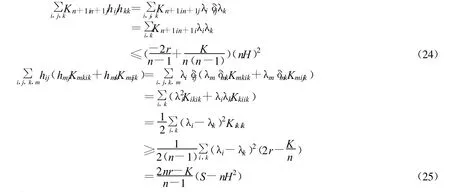
令hij=λiδij，则选取适当的基使得hij=λiδij

(26)式证明如下

最后，利用引理1和(10)，将引理1的第一式改写为

将此式两端关于指标i求共变导数，并关于i求和，得

调整指标，结合引理1的第二式，可得

其中ω定义在Mn上的1-形式

因为Mn具有常平均曲率，得

由(17)式，得

从而有(22)-(32)，有

由于Mn是紧致的，将(33)两端积分，利用Green散度定理，即得定理1的证明。

[1] EELLS J，LEMAIRE L.Selected Topics in Harmonic Maps[M].CBMS 50，AMS，1983.

[2] 姜国英.Riemann流形间的2-调和映照及其第一，第二变分公式[J].数学年刊，1986，7A(4):389-402.

[3] 姜国英.Riemann流形间的2-调和等距浸入[J].数学年刊，1986，7A(2):130-144.

[4] 欧阳崇珍.伪黎曼空间型的2-调和类空子流形[J].数学年刊，2000，21A(6):649-654.

[5] 宋卫东.关于局部对称空间中2-调和子流形[J].应用数学，2002，12(1):25-29.

[6] 宋卫东.关于局部对称伪黎曼流形中的2-调和类空子流形[J].系统科学与数学，2007，27(2):170-176.