基于改进微分进化算法的节能减排发电调度研究

饶 攀，彭春华

(华东交通大学电气与电子工程学院，江西南昌330013)

为响应当前我国电力行业“节能减排”的号召，改变常规的仅按购电成本最小化为目标进行发电机组的经济调度，综合考虑各电厂的能耗、污染物排放以及全网网损，按照电力系统总能耗、总污染排放量尽量低的原则，建立电力系统节能减排发电调度多目标优化模型。由于该模型具有高维数、不光滑、非线性、各目标函数之间相互冲突和约束条件难以处理等特点，决定了求解的复杂性。而传统的多目标问题的求解通常是将多目标问题转化为单目标优化问题进行简化，虽然降低了求解的复杂程度，但是具有很大的局限性，最终所求的解并不是真正意义上的符合全局意义的最优解[1]。近年来，多目标进化算法(Multi-Objective Evolutionary Algorithm，MOEA)利用其随机搜索能力找到最优解集的优点被广泛研究和使用。其中，最常用的MOEA之一的NSGA-II算法，成为了第二代MOEA的标志[2]。

然而，由于NSGA-II算法采用的是遗传算法的交叉和变异策略，遗传算法本身存在收敛性不稳定，速度慢和容易早熟等缺点，因此NSGA-II算法同样也存在着这些不足。基于此，本文将引入改进型微分进化算法代替NSGA-II中的遗传操作;由于NSGA-II算法非劣排序操作通常都是基于目标空间，实际计算中并不能保证能够得到真正pareto非劣解，因此本文提出一种有效地基于小生境的排挤机制对其进行改进;由于微分进化算法中的缩放因子F、交叉概率CR等参数都会在一定程度上影响着DE算法的收敛速度和搜索性能，为了避免算法收敛速度下降或者是搜索性能的降低，本文基于粒子群算法中惯性权重动态调整的思想，提出了对参数F，CR采用随机进化动态调整的策略[3]。

本文基于INSDE算法对模型进行求解。结果表明该算法能够克服传统多目标进化算法的缺点，使得求解速度、抗早熟性、收敛特性等方面都有明显的改进，可以得到满足条件的节能减排发电调度最优解集。

1 节能环保发电调度多目标优化模型

1.1 发电煤耗(发电成本)目标函数

在符合国家产业政策的前提下，使得电网中所有的发电机组总的发电煤耗最小。在本文中按照市场经济的客观规律，努力争取总电成本最低。在NG个发电厂组成的一个系统中，电厂i的上网电价为ri，系统总购电成本C的目标函数为[4]式中:Pi为分配给电厂i的发电量。

1.2 有害气体排放量目标函数

电厂排放有害气体主要包括CO2，SO2，NOi等，各气体排放量和发电量的关系可以单独建立模型，本文采用有害气体综合排放模型，有害气体排放总量E的目标函数为[5]

式中:αi，βi，γi，ξi，λi均为发电厂i的污染气体排放系数。

1.3 约束条件

不等式约束:

(3)式为发电约束，P min和P max为发电单元i的最小发电量和最大发电量，单位为MW。

等式约束:

(4)式为电量平衡约束，式中PD为系统总负荷需求。由于网损大小在一定程度上也能体现节能发电调度的效益，并且网损是客观存在的，并不能忽略不计。式中的Ploss为系统的总网损。本文采用式(5)表示:

式中:Bij为电厂i和电厂j之间的网损系数。

综合以上两个目标函数式(1)和(2)，以及约束条件式(3)和(4)，即为节能环保发电调度多目标优化模型。而寻求一种能求解该模型最优解集的多目标优化算法是本文研究的重点。

2 改进非劣排序微分进化算法(INSDE)

本文提出的改进非劣排序微分进化算法(INSDE)由两个部分组成:其一基于NSGA-II的非劣排序，其二子代的微分生成方式。

2.1 排挤机制的改进

在传统的NSGA-II算法的pareto非劣排序操作的过程中，对于同一pareto非劣等级中的个体，通常通过计算群体中每个个体的聚集距离，然后根据聚集距离定义一个偏序集，构造群体时依次从偏序集中选择个体。若设个体B的前后相邻两个体分别为A和C，在NSGA-II算法中，个体B的拥挤距离(稀疏度)DC(B)计算式定义如下

其中:fi(A)与fi(C)分别为个体A和C在第i个目标函数上的值。

此计算式虽然简单快速，但存在较大局限性。它只考虑了前后相邻两个体A和C间的距离，但没有考虑个体A，B和C三者之间的分布特性。为此，有学者对此进行改进。设个体A和C的中心点为O，将处于A和C之间的个体的拥挤距离DC(B)改进为[6]

式中:fi(B)与fi(O)分别为个体B和邻域中心O在第个目标函数上的值。

式(7)能综合反映出个体B的稀疏度既与其在各目标函数上的邻域大小有关，又与分布均匀程度有关。它虽然在一定程度上保证了解的多样性和分布性。但是鉴于NSGA-II的排序机制是基于目标空间的。在实际计算中，可能会保留一些极端解。这些极端解是不可行的，与pareto前沿差别很大，占据了空间，降低了进化效率，增加了进化成本且收敛不到pareto前沿。原因在于排序机制不完善导致不可行解得以保存而降低了进化效率。

传统的排挤机制由于是基于自变量空间内的“距离”而进行排挤，对之无能为力。单纯从改进排挤距离出发是很困难的。

本文中，基于小生境排挤机制的实现提出如下的改进:在确定的每个pareto等级中，先按照其中一个目标函数值大小依次排列，找出该非劣前沿的两个极值端点，求出它们的欧氏距离dist0，n，确定阈值δ=dist0，n/2◦popsize。比较当前非劣前沿中的任意两个个体，若两个个体间的欧氏距离小于或者等于临界距离δ。采用小生境策略，以阈值δ作为小生境半径δshare，修剪掉该前沿中的不合理的个体。若阈值δ=0，即为该非劣前沿中只有一个个体，鉴于不同等级的非劣前沿的代表性，则该个体直接保留。实验结果表明，这一改进，改善了群体的多样性，提高了进化效率。

2.2 微分进化算法改进

微分进化算法(DifferentialEvolution，DE)是由Rainer Storn和Kenneth Price为求解切比雪夫多项式而于1995年提出的一种基于种群的全局随机搜索算法。DE的原理简单，受控参数少，实施随机、并行、直接的全局搜索，易于理解和实现。DE已成为一种求解非线性、不可微、多极值和高维的复杂函数的一种有效和鲁棒的方法。本文不再阐述DE具体步骤。

在标准DE算法中，变异操作的三个个体可以随机选择，也可以从非劣集中选择一个最优个体作为基矢量。对应不同的个体选择方法，对于种群规模为Np，第G代每个目标个体向量，一般可按照式(8)，(9)等方式进行变异操作产生中间个体Yi，G+1。

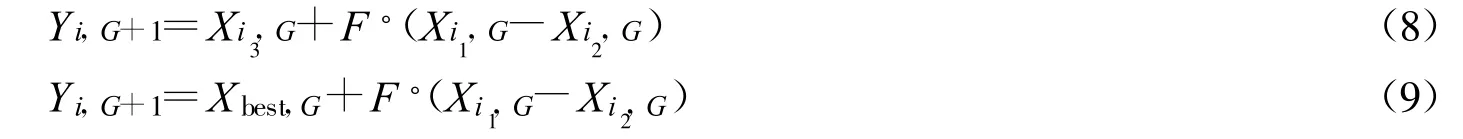
式(8)的选择方式虽然改善了搜索结果，但是降低了DE的收敛速度。而按照式(9)的选择方式提高了收敛速度，但是限制了它的搜索能力。在改进的微分进化算法(INSDE)变异操作用最优竞争集代替随机选择的基矢量。在3个随机变量Xi1，G，Xi2，G，Xi3，G中选择最优的一个作为基矢量，其余两个用来做差分矢量。该操作对每一个变异点在最优竞争集领域进行搜索，保证了算法搜索特性的同时加快了收敛速度。具体操作为

在DE算法中，控制参数的合理设置也是一个十分重要的问题。F，CR过大，或者过小都会影响到算法的收敛性。在改进的微分进化算法(INSDE)中，F，CR采用随机动态策略。而不是像标准DE中采用固定值。当搜索点位于全局最小点周围形成的解空间簇时，在保持快速收敛的情况下，这个随机定位特性使得它本身逐渐转化成强大的搜索能力[7]。

式中:CRmax，CRmin为设定的交叉因子的CR的最值;λmax，λmin分别为设定的最大迭代次数和当前迭代次数;F max，F min为设定的比例因子F的最值。

以上两点改进就是基于NSDE的改进微分进化算法(INSDE)。具体操作，参考实例仿真。

3 算例及其分析

为讲解INSDE算法的流程与具体操作，并验证本文改进微分进化算法的有效性。以一个6发电厂的电力系统进行节能，减排发电调度。每个发电厂的发电上下限、上网电价、发电厂间的网损系数以及各机组参数见表1、表2[8]。系统总负荷为700MW。

本文分别采用NSGA-II，NSDE，以及INSDE对该多目标问题进行求解。

以下为INSDE的具体操作流程:

第一步:初始化。在各发电单元出力范围内随机生成P1，P2，…，P6，分别表示发电厂1，2，…，6的初始出力。再代入式(5)中计算网损。当越接近总负荷时，则Ploss应该越小，反之，就会越大。基于此原理，本文采用等式约束的处理方法来解决个体的电量不平衡问题:

第二步:代入式(1)，(2)中计算目标函数值。

第三步:非劣排序。对初始化生成的种群按照pareto非劣排序策略，找出当前种群的所有不同pareto非劣前沿，并且采用本文的改进的排挤机制对同一非劣前沿中的个体进行排序和修剪。

然后进行以下的循环操作:

第四步:采用锦标赛选择方法从排序后的群体中选择出最优的个体，形成新的种群。

第五步:改进微分操作，对以上种群采用式(10)变异机制，得到新的子种群。

第六步:种群混合。为了保持个体多样性，将非劣排序后的种群与微分进化后的种群混合成一个更大的临时种群。

第七步:非劣排序。对临时种群进行非劣排序操作。

第八步:重组。对上述种群进行重组，重新选择个体，形成一个新的群体。

循环直至最大迭代次数终止。

表1 发电单元各项参数

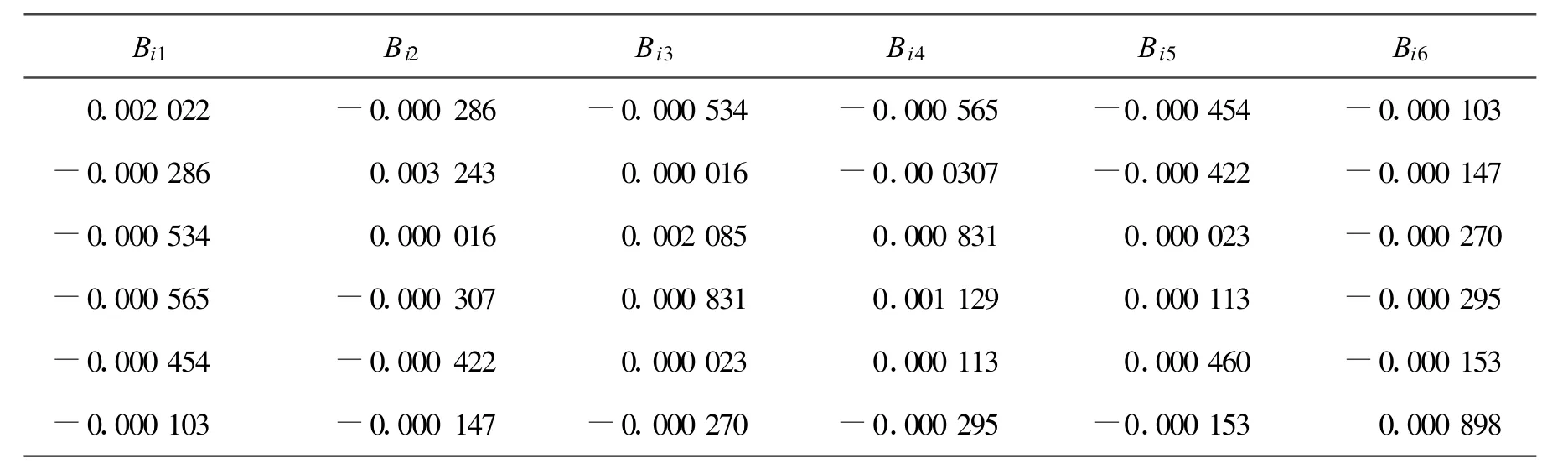
表2 网损系数Bi

以下分别为NSGA-II，NSDE，以及INSDE对该多目标问题进行求解的结果。其中，NSGA-II算法中的最大迭代次数为10 000，此时规模为100，遗传，交叉概率分别为0.95，0.05。NSDE，INSDE的CRmax，CRmin分别为0.9，0.4。Fmax，Fmin分别为0.9，0.3。种群规模为100，最大迭代次数为2 000。得到的非劣前沿图为图1所示。

从对比的非劣前沿图中可以很明显的看出本文所设计的改进微分进化算法(INSDE)相比于常规的NSGA-II，在寻优速度上有明显的改进，INSDE只需要迭代2 000次就可以得到图1的pareto前沿，并且得到的非劣前沿也有明显的改善;相比于NSDE，INSDE算法得到的pareto前沿更完整，更逼近真正的非劣前沿，以及非劣解的分布更加均匀。

从非劣前沿分布较均匀的区域随机选取一组非劣解，得到三种算法的发电调度最终优化结果。表3中的优化结果表明，算法INSDE得到的最优解保证污染气体总排放量和总购电成本两个目标函数均小于NSGA-II和NSDE得到的解。说明INSDE得到的解才是pareto最优解。同时INSDE算法得到的网损最小，满足节能减排发电调度的要求。

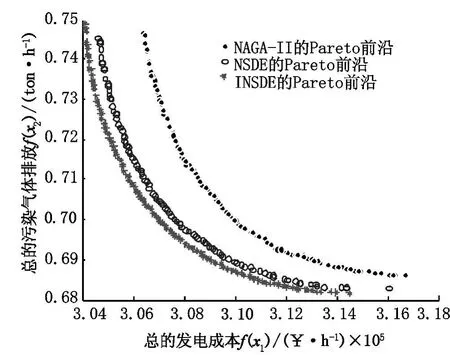
图1 三种算法的Pareto前沿比较

表3 发电调度优化结果

4 结论

本文提出的INSDE算法是基于NSGA-II中的pareto非劣排序的改进和微分进化算法中的变异机制改进的有机融合。充分考虑了不同电厂的上网电价和排污系数的差异的前提下，实现了总发电成本和总的污染物排放均尽量小的多目标节能，减排发电调度问题的求解。该算法体现了优越的性能，简单、快速地寻找到完整、均匀的全局多目标pareto解集。

[1] 郑金华.多目标进化算法及其应用[M].北京:科学出版社，2007.

[2] 陈小庆，侯中喜，郭良民.基于NSGA-II的改进多目标遗传算法[J].计算机应用，2006，26(10):2 453-2 456.

[3] 周清清，刘勇.多目标微分进化算法的实现[J].自动化仪表，2009，30(12):6-11.

[4] ABIDOM A.Environmental/economic power dispatch usingmu ltiobjective evolutionary algorithms[J].IEEE Trans on Power Systems，2003，18(4):1 529-1 537.

[5] WANG L，SINGH C.Environmental/econom ic power dispatch using a fuzzified multi-objective particle swarm optimization algorithm[J].Electric Power Systems Research，2007，77(12):1 654-1 664.

[6]彭春华，孙惠娟.基于非劣排序微分进化的多目标优化发电调度[J].中国电机工程学报，2009，29(34):71-76.

[7] 杨艳，戴朝华.基于微分进化算法的电力系统最优潮流[D].成都:西南交通大学，2009.

[8] RUGHOOPUTH H，KINGAH.Environmental/econom ic dispatch of thermalunits using an elitistmultiobjective evolutionary algorithm[C]//Proceedings of 2003 IEEE ICIT，Maribor，Slovenia，2003，1:48-53.