上海地区重力式防汛墙抗震稳定性研究

耿大新，杨林德

(1.华东交通大学土木建筑学院，江西南昌330013;2.同济大学，地下建筑与工程系，上海200092)

国内外许多地震学家和工程地震学家就墨西哥地震(1985年9月19日，Ms7.8)、日本阪神地震(1995年1月17日，Ms7.2)等造成如此巨大的伤亡和财产损失进行研究，发现地表软土覆盖层引起地震动明显放大，使振型频率落在地震动放大频段内的建筑物遭受的破坏比基岩处大得多[1]。上海市区软土地层厚达250～300m，发生地震时易由此加大危害。近年来大量的学者对上海地区的软土及其地震响应进行了大量的研究。杨超、杨林德、季倩倩[2-4]等人结合饱和软黏土进行的动三轴试验，利用边界面模型理论建立了软黏土的黏弹塑性动力本构模型，并结合地铁振动台试验对上海地铁车站的动力响应进行了细致的分析。黄雨[5，6]等人基于一维场地地震反应的等效线性化频域分析方法，建立了上海软土场地的动力分析模型，以ElCentro地震波为例，重点分析了上海地区场地土的地震反应加速度反应和频谱特征。楼梦麟[7]等人应用模态摄动法求解水平分层均匀土层的地震反应，通过大量的数值计算，讨论上海软土土性变化对土层基本周期和表面地震加速度反应的影响。周健[8]等人在软土室内动力试验和有限元有效应力动力反应分析基础上，考虑软土振动孔压上升及消散、震陷、土-结构动力相互作用，研究了地下结构地震土压力的简化算法。防汛墙系修筑在河道两侧的挡水构筑物，是上海市抗洪减灾的生命线工程。地震来临时，地基的振动引起水、土、结构的振动，由于三者自振特性的差异，使之不能同步振动，从而引起附加的动水压力和动土压力。然而近年的研究多集中在软土动力特性及地下或地表结构的动力响应，岸墙属半埋地下结构研究较少。但从以往多次地震调查来看，岸墙在经历一次或多次地震后发生破坏是一个比较突出的问题，它不但带来大量的经济损失和人员伤亡，而且有可能引发次生灾害。因此有必要结合土质条件对其抗震稳定性开展研究。本文拟以重力式防汛墙为例，将之简化为二维平面应变问题，在考虑水-土-结构相互作用的基础上，采用直接动力时程分析，探讨饱和软土地区防汛墙地震动力反应的特点，并评估墙体的抗震稳定性。

1 防汛墙结构体系动力分析基本方程

1.1 基本假设

防汛墙前水体较小，动水压力对结构地震响应的影响较动土压力的影响要小。墙体的破坏大都是由于土压力过大或土体液化等因素引起的。本文拟对水体按不可压缩模型处理，将土体视作固液两相介质，采用Biot动力固结方程描述饱和软粘土的性态，在土体与结构之间设置接触面，以此模拟水、土、结构间的动力相互作用对重力式防潮汛墙结构整体抗震稳定性的检验，结合动力计算结果研究防汛墙结构的整体抗滑稳定性安全系数的变化规律。为简化分析，作如下假设:

(1)防汛墙结构在轴线方向的长度足够大，可以作为平面应变问题进行研究;

(2)防汛墙结构位于深度有限的土层中，土层下方为基岩，地震波自基岩面垂直向上输入，基岩运动为水平、垂直两向运动;

(3)防汛墙前水体不可压缩，结构不透水，不产生孔隙水压力。

1.2 动力平衡方程

在地震荷载作用下，防汛墙结构体系的动力响应是一个典型的流固耦合问题。结构的动力反应虽然复杂，但仍可简化成一个多自由度体系，其振动方程可利用Lagrange方程[9]得到。设q分别代表整个结构的结点位移向量和结点速度向量，以p表示水作用于墙体各节点的动水压力向量。以T，V表示防汛墙结构体系的动能和势能，则有

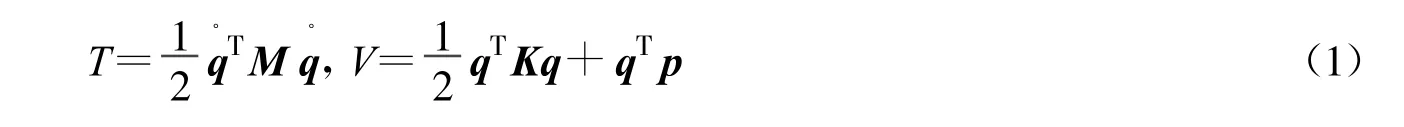
式中:M为结构体系的质量矩阵;K为结构体系的刚度矩阵。

从式(1)可以看出，势能中除固体的应变能外，增加了动水压力做的功。在受迫振动的情况下，应当考虑结构体系的阻尼力的作用。假设阻尼力fs的大小与应变速度成正比，即

则非保守力做的总虚功δWnc可以写为

式中:F为结构承受的外荷载向量。

由于水体的不可压缩性，其连续性方程为

假定由于墙体振动引起的水流扰动为无旋运动，则必存在扰动速度势φ(x，y，z，t)，它与流速的关系为

把式(6)代入(5)，得

由式(7)可以看出，扰动势函数满足拉普拉斯方程。略去对流项与粘性项后，由非恒定流的伯努利方程可得压强p与φ之间的关系为

由式(7)、(8)可知，扰动压强p也满足拉普拉斯方程，即

对于防汛墙结构体系，边界条件如下。

墙体临水面，临水墙面与该处的水具有相同的法向速度，即有

式中:vn，f为墙面任一点的法向速度，它在墙面是连续函数。

在水面处，不考虑扰动流引起的水面波动，则在水面上恒有

河底，假设河底为刚性层，不考虑淤积层的吸收作用，有

当水离墙很远时，水流的扰动压强应趋于零，所以有

式中:x为防汛墙墙面的法线方向，指向水体一侧。

式(7)～(13)为动水压力的控制方程组。

墙面节点动水压力向量p f可表示为墙面节点加速度的线性组合，即:

式中:D为动水压力影响矩阵;Dij表示在迎水面第j结点沿某一坐标轴方向施加单位加速度时在第i结点处引起的动水压力值。显然，D的维数远低于质量阵M的维数为防汛墙临水面结点的加速度向量，对于空间问题，一个节点有三个方向的加速度分量。

式(4)中的pf是作用在墙面上的动水压力向量，为了转换成式(4)中的节点力向量，需乘一维数转换矩阵s，即

令:

式中:ΔM为动水压力形成的附加质量阵，为非对角阵的满阵。

将式(16)和(17)代入式(4)得

式(4)及式(18)均为防汛墙结构体系的动力平衡方程。从式中可以看出，当不考虑水的压缩性，采用集中质量法求解时，动水压力的作用可简化为相应结点上的附加荷载或附加质量阵。由于动力问题的复杂性，因此拟对防汛墙的动力模拟采用数值模拟，计算时将动水力以附加荷载形式施加于相应的质点上。

2 工程概况及计算网格

2.1 计算网格

典型的重力式防汛墙结构如图1所示，水体通常水位为+2.20 m，地震高水位为+5.74m，地震低水位为+0.76m。由图可见防汛墙结构与半无限地层相连，横剖面上左、右及下部边界均在无穷远处。确定计算范围时，在水平方向拟将水体一侧取为20m，土体一侧50 m;竖向上表面取至地表及河底，河底坡度为1∶6，底部取至地质钻孔的孔底标高-20m，沿纵轴线方向取为1m。采用FLAC2D进行计算，数值模拟中，对地层土体及防汛墙结构均采用四边形实体单元进行离散;墙前护坡采用梁单元模拟，在结构与土体、护坡与河底的接触面上则设置了接触面单元，计算网格如图2所示。

图1 典型重力式防汛墙结构简图

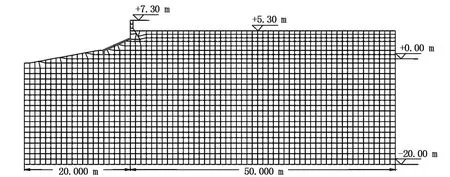
图2 典型重力式防汛墙计算网格

2.2 边界条件

防汛墙结构抗震稳定性分析的计算同时包括静力计算和地震动力分析。静力计算主要形成地基中的自重应力场，计算时两侧采用水平约束边界，下部采用竖向约束边界。地震动力分析时，由于采用有限长度的地层模拟半无限地层，两侧边界均取为自由场边界，即在计算网格的两侧边界处各增设一列与边界等高的粘性网格，通过其与静力边界的耦合作用模拟周边外延介质对能量的吸收特性。粘性网格提供的不平衡力直接施加在主网格的边界上，用于吸收地震波保持其不反射性;下部边界输入地震波，考虑上海软土对高频波的滤波作用及对低频波的放大作用，地震波采用以低频为主最大加速度为0.1 g的上海人工波[10]，如图3所示，竖向地震波取为水平向地震波的1/2。

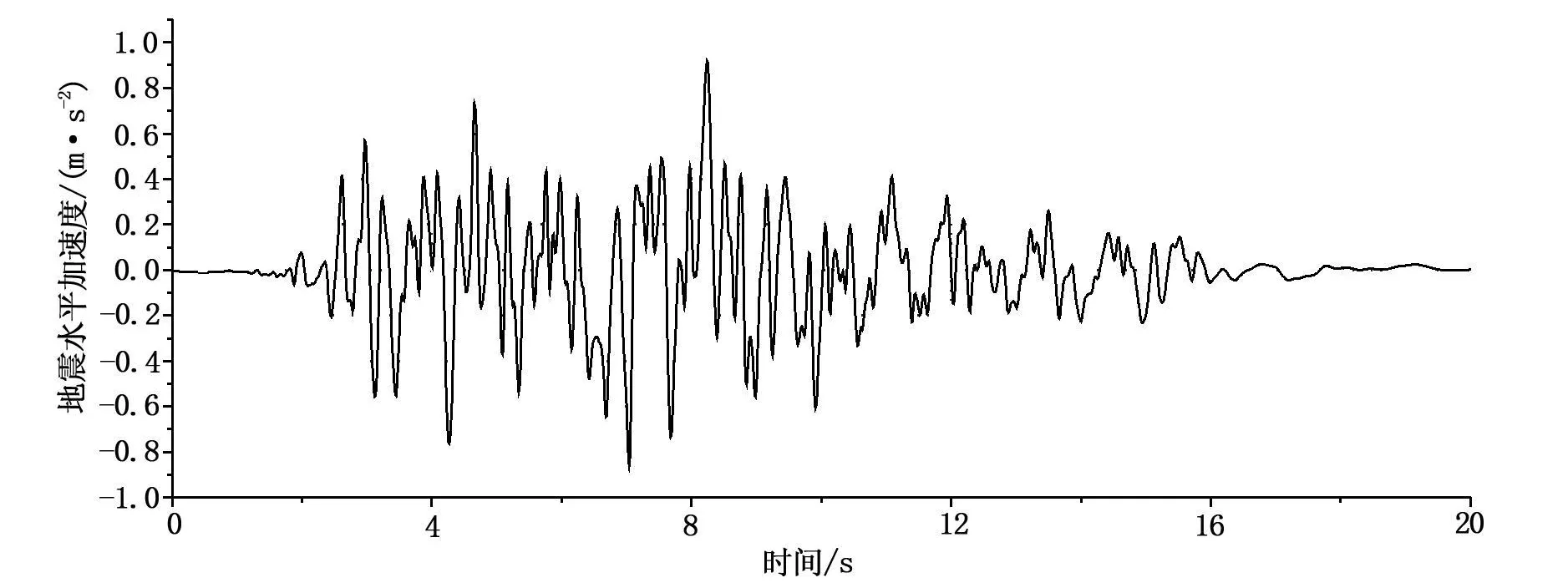
图3 水平向输入地震波加速度时程曲线

2.3 计算参数

饱和软土可简化为土骨架和孔隙水组成的两相介质，在动荷载作用下孔隙水压力上升，土骨架的有效应力降低，土的性状发生变化，饱和软粘土在动荷载作用下的变形特性十分复杂，特点为在很低的应力水平下即进入弹塑性状态，同时即使在应变趋于零时也存在能量耗散，阻尼比并不趋向于零。基于上海典型软土土层动力试验数据[2，4]，拟采用Davidenkov模型描述上海软土的非线性动力特性土体材料的动力本构模型，其本构关系为

式中:Gmax和λmax为最大动剪模量和最大阻尼比;γ0为参考应变;A、B均为回归参数，与土性有关。

表1 典型防汛墙地基土体的动力特性参数[10]

3 计算结果与分析

地震波在向上传播过程中有明显的放大效应。通常水位下，地表反应加速度的峰值出现在地震发生后8秒左右，大小约为180 gal;但墙体加速度的反应波较土体而言，主频较高，加速度峰值也出现在地震发生后8秒左右，幅值则约为210 gal。

在地震高、低及通常3种水位情况下，作用在墙体一侧的动土压力值相差不大，且均近似随深度成线性关系增加，增幅约为静止土压力值的35%左右。地震结束后，作用在墙体上的土压力较静止土压力有所增大，增幅在10%左右。

墙体在地震过程中位移较大。墙顶及墙底的位移如表2所示，3种水位情况下墙体的位移量虽然不同，但变化时程图非常相似;地震结束后均有残余位移存在，墙体有绕趾部前倾的趋势;就整个防汛墙体系而言有整体滑移的危险，地表达到最大加速度以后的1秒内，防汛墙的整体稳定性迅速下降，最小安全系数仅为0.7左右，出现在地震发生后9秒左右。图4给出通常水位情况下墙顶的位移时程。图5给出了墙体的残余变形及墙体的破坏趋势，图6给出防汛墙体系最小安全系数的变化时程。

表2 重力式防汛墙地震动力反应特征位移值

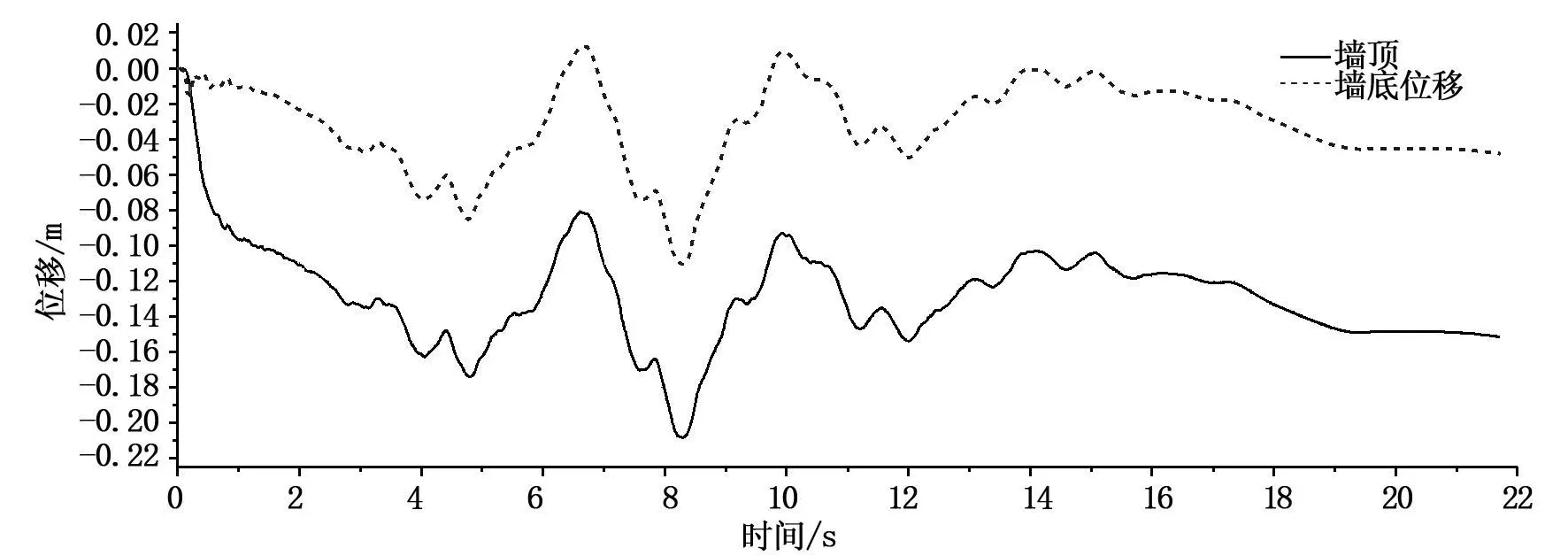
图4 通常水位情况下防汛墙墙体位移时程图(位移以背离河道为正)

图5 通常水位情况下重力式防汛墙残余变形图(变形放大10倍)

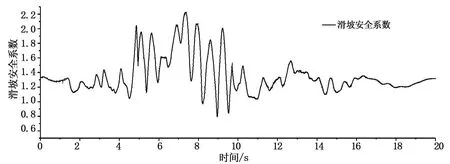
图6 通常水位情况下重力式防汛墙整体稳定安全系数变化时程

由以上分析可以看出，重力式防汛墙的抗震(抗滑移)稳定性明显不符合设防要求，年修时宜在墙趾前贴墙增设板桩将其加固，新建或改建时不宜再采用这类防汛墙。

4 结论

本文考虑了水-土-结构的相互作用，对一典型的重力式防汛墙进行了有效应力数值模拟，得出了以下结论:在地震作用下，墙体会向水体一侧发生较大位移，有前倾的趋势，并会有残余位移出现。在地震过程中，结构体系的整体稳定安全系数随地震加速度(方向指向河体一侧)的增高而减小，但有一定的滞后效应。在地表最大反应加速度过后1秒内，整体稳定安全系数降到最低，不足1，结构有发生整体滑移的危险。在不同水位的情况下，墙体的地震反应有较大的不同，这主要体现在墙体的位移量和整体稳定安全系数上。从结果来看，当河床处于高水位运行时，防汛墙的抗震稳定性比通常水位和低水位情况高。

[1] 徐永林，熊里军.上海地表软土层、细砂层的地震波反应[J].中国地震，2003，19(1):84-88.

[2] 杨超，杨林德，季倩倩.软黏土在循环荷载作用下动力本构模型的研究[J].岩土力学，2006，27(4):609-614.

[3] 杨林德，杨超，等.地铁车站的振动台试验与地震响应的计算方法[J].同济大学学报:自然科学版，2003，31(10):1 135-1 140.

[4] YANG LD，WANGG B，etal.A study on the dynamic properties of soft soil in shangha[J].Soil and Rock Behavior and Modeling:GSP 150，2006，194(62):466-473.

[5] 黄雨，周红波.上海软土的动力计算模型[J].同济大学学报:自然科学版，2000，28(3):359-363.

[6] 黄雨，叶为民，唐益群，等.上海软土场地的地震反应特征分析[J].地下空间与工程学报，2005，1(5):773-777.

[7] 楼梦麟，严国香，沈建文，等.上海软土动力参数变异性对土层地震反应的影响[J].岩土力学，2004，25(9):1 368-1 372.

[8] 周健，董鹏，池永.软土地下结构的地震土压力分析研究[J].岩土力学，2004，25(4):554-559.

[9] CLOUGH RW，PENZIEN J.Dynamics of structures[M].New York:McGraw-Hill Inc.1975:99-134.

[10] 祝龙根，杨林德，等.上海地铁区间隧道地基土动力性质试验研究[R].上海:上海防灾救灾研究所，2000:23-65.