基于粗糙集和神经网络的柴油机故障诊断

田静宜，潘宏侠，杨 业，杨丽金

（1.中北大学机械工程与自动化学院，太原030051；2.山西平遥减速器厂，平遥031100）

1 引言

柴油机缸盖的振动信号中，包含了故障特征和其它干扰信号，通过试验方法提取的特征参数往往不完备、冗余，这给后续故障诊断处理带来了困难。如何在不缺失信息量的情况下，用较少的属性值就能有效实现柴油机的故障诊断，是一个亟待解决的问题。

小波包分析，将频带进行多层次划分，提高了时频分辨率。信号经小波包降噪后，再利用时域、频域分析，可以构造出有效的特征值。人工神经网络(ANN)具有可学习性和并行计算能力，可以实现分类、自组织、联想记忆等功能。粗糙集（RS）理论是一种刻画不完整性和不确定性的数学工具[1～2]，它能有效地分析和处理不完备信息，可以弥补神经网络无法判断冗余知识，以及训练时间过于漫长的局限性。本文以某型号大功率柴油机为例，把小波包分解、粗糙集理论和人工神经网络有机地结合起来，用于研究故障诊断问题，目的是提取效果更加明显的特征值，应用ROSETTA软件约简特征属性，从而提高故障诊断的效率。

2 粗糙集理论及ROSETTA软件

2.1 粗糙集的重要理论

（1）知识与分类

粗糙集的主要思想是在保持分类能力不变的前提下，通过知识约简，导出问题的决策或分类规则[3]。在分类过程中，将相差不大的个体归为一类，它们之间的关系即为不可分辨关系（记为IND）。设U是对象组成的非空有限集合（论域），R是U上的等价关系。若对任意子集X∈U，称X为U中的概念或范畴，则U中的任意概念族称为U中的知识，K=(U,R)称为知识库。对于任意x,y∈U且(x,y)∈R，称对象x和y在K中是不可分辨的，R被称为一个不可分辨关系。

（2）知识的约简与核

约简和核是粗糙集理论的核心内容之一，约简是在保持知识库分类能力不变的前提下，删除其中不相关或不重要的知识。设Q R，如果Q是独立的，且IND(Q)IND(R)，则称Q为R的一个约简。根据不可分辨关系，R可以有多种约简。R中所有必要关系组成的集合称为R的核，记作CORE(R)，CORE(R)=∩RED(R)。

2.2 ROSETTA软件

2.2.1 ROSETTA简介

ROSETTA是由挪威科技大学计算机与信息科学系和波兰华沙大学数学研究所合作开发的一个基于粗糙集理论框架的表格逻辑数据工具，它提供了多种数据预处理功能，如决策表补齐、决策表离散化等，同时还有粗糙集中常见的约简和规则的获取算法[4]，因此它支持从数据预处理到预测和分析规则的全过程。系统提供的主要功能有数据获取与结果输出、数据预处理（决策表补齐、离散化等）、计算（约简）、其它功能等。ROSETTA在上述每一个功能中提供了多种算法可供用户选择，是一个很好的粗集理论实验平台。

2.2.2 ROSETTA离散化方法

目前，试验中获得的数据大多是连续值，而在粗糙集理论中，对数据的约简是建立在离散数据表的基础之上，因此，对连续属性进行离散化是对实值属性的决策表进行预处理的关键步骤之一。对连续属性进行离散化，就是将数值属性的属性值划分成若干个子区间，并以此区间代替原有的实值，从而使决策表泛化。连续数值的离散化方法很多，在ROSETTA软件中有Naive算法、Semi-Naive算法以及布尔推理算法等。

（1）Naive算法

Naive算法对每个属性，根据属性值由小到大的顺序对决策表中的实例进行排序，然后进行判断，对于两个相邻实例，在属性表和决策值都不同的情况下，选取两个属性值的平均值作为断点值。该算法根据具体的条件属性值和决策属性值选取断点值，而不是盲目的选取，但没有考虑信息系统的不可分辨关系。Naive算法选取断点的过程是一开始设断点集为空集，逐步增加断点得到离散化结果，得到的断点数目很多。

（3）Semi-Naive算法

Semi-Naive算法在Naive算法的基础上，通过对每个由Naive算法得到的断点的两个相邻属性值所属的等价类所对应的决策中出现频率最多的决策值的集合是否存在包含关系进行判断，从而决定是否选取此断点，若两个集合存在包含关系，则不选取此断点，否则选取此断点。

（3）布尔推理算法

此种算法的思想是首先在保持信息系统的不可分辨关系不变的前提下，尽量以最小数目的断点把所有实例间的分辨关系区分开。

2.2.3 ROSETTA约简算法

决策表属性的约简过程，就是从决策表系统的条件属性中去掉不必要或不重要的条件属性，从而得到决策规则。通过对决策表中的条件属性进行简化，使得简化后的决策表具有与简化前的决策表相同的功能，但条件属性数目更少。ROSETTA软件环境下提供的约简算法有遗传算法、Johnson算法等。

3 基于粗糙集的柴油机缸盖振动信号的故障诊断

3.1 信号消噪和特征值提取

（1）小波包信号消噪

柴油机的工作环境比较恶劣，试验中测得的振动信号往往包含了大量的噪声信号，应用小波包分解进行降噪处理，可以减少干扰噪声对结果的影响[5]。图1和图2为经过小波包消噪处理前后的对比图，从图中可以看出来，经过小波包降噪后，冲击信号的幅值普遍降低。

（2）时域、频域分析

柴油机是一种典型的往复运动机械，振动激励源多。其缸盖的振动信号受到很多因素的影响，表现形式非常复杂，既有周期特性，又有非平稳时变及某些冲击特性。图3为单个周期内，正常工况下，柴油机缸盖某测点处实测振动信号的时域波形。

信号的时域、频域特征值能够反映信号幅值的大小、波动的变化以及能量的分布规律。针对柴油机表面振动响应信号，选取整周期的信号进行时域、频域分析，提取特征参数，并归一化作为神经网络的输入向量。

3.2 故障诊断方法

人工神经网络是一种大规模的分布式并行处理系统，具有自组织、自学习、容错性等特性，对于解决复杂的非线性问题具有广阔的应用前景，常规BP算法存在收敛速度慢和容易陷入局部极小点等问题，因此本文选用RBF神经网络作为故障诊断系统的诊断模型。图4为单隐层前馈RBF神经网络模型[6]，它包括输入层、隐层和输出层，将故障征兆作为输入层节点，故障原因作为输出层节点，通过样本集的训练学习，确定网络结构，并根据此故障征兆识别出柴油机的相应故障状况。

3.3 基于粗糙集的故障诊断系统

基于ROSETTA的柴油机缸盖振动信号故障诊断系统，具体实现步骤如下：

1）测量柴油机在正常工况和几种故障工况下缸盖处的振动信号，并对其进行小波包降噪和时域、频域分析，形成特征值样本集。

2）应用ROSETTA软件，对振动信号的特征值进行离散化处理。

3）用离散化后的条件属性和决策属性建立决策表并使其相容。

4）用粗糙集理论对条件属性化简：（1）删除决策表中相同的规则，即重复的实例；（2）计算去掉一个条件属性后的不可分辨关系，若相同则删除表中该多余的条件属性；（3）删除分类规则中的多余属性，求出属性的核和约简。

5）利用优化的属性组合，将简化后的条件属性作为RBF网络的输入，柴油机故障类型作为输出，隐含层选择高斯函数，采用RBF，神经网络进行故障模式分类。

4 试验

4.1 特征参数的提取

针对大功率柴油机运行工况复杂、故障排除困难的实际情况，对某12V柴油机典型故障工况下的振动信号进行测试。试验设置了正常和8种故障状态、4种转速、22个测点位置，进行振动信号的测量，本文选取其中1个测点在1种转速下正常和3种故障工况的振动数据进行分析，每种工况选取6个样本，共24个样本（Y1，Y2，…，Y24），测点位置为右侧第6缸缸盖上侧，转速为1 800 r/min，4种工况分别为：正常工况（A）、右侧第6缸喷油器渗漏（B）、右侧第6缸喷油器断油（C）、左侧第1缸和右侧第6缸双缸断油（D）。

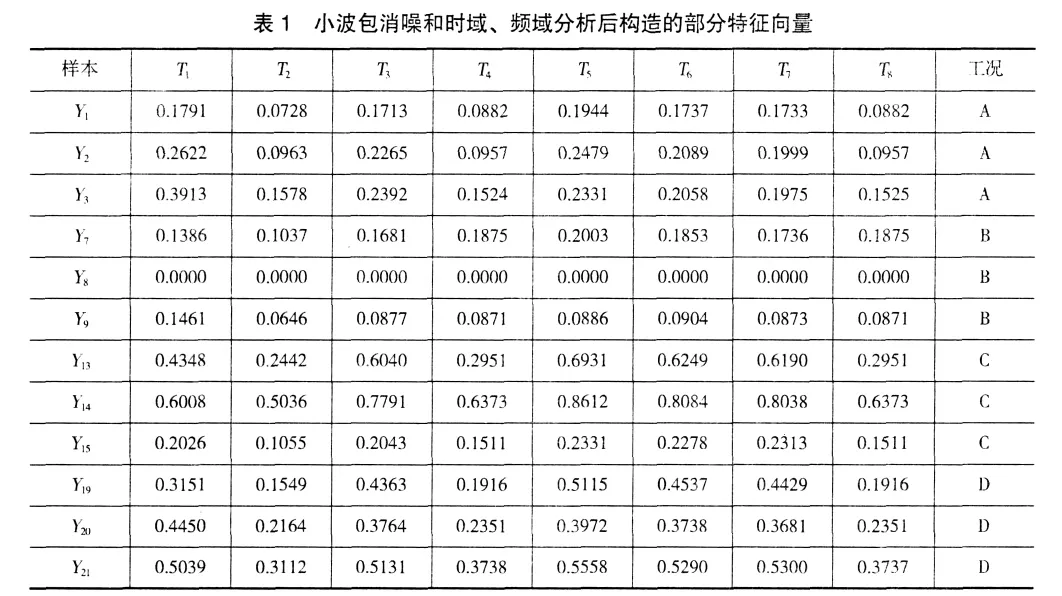
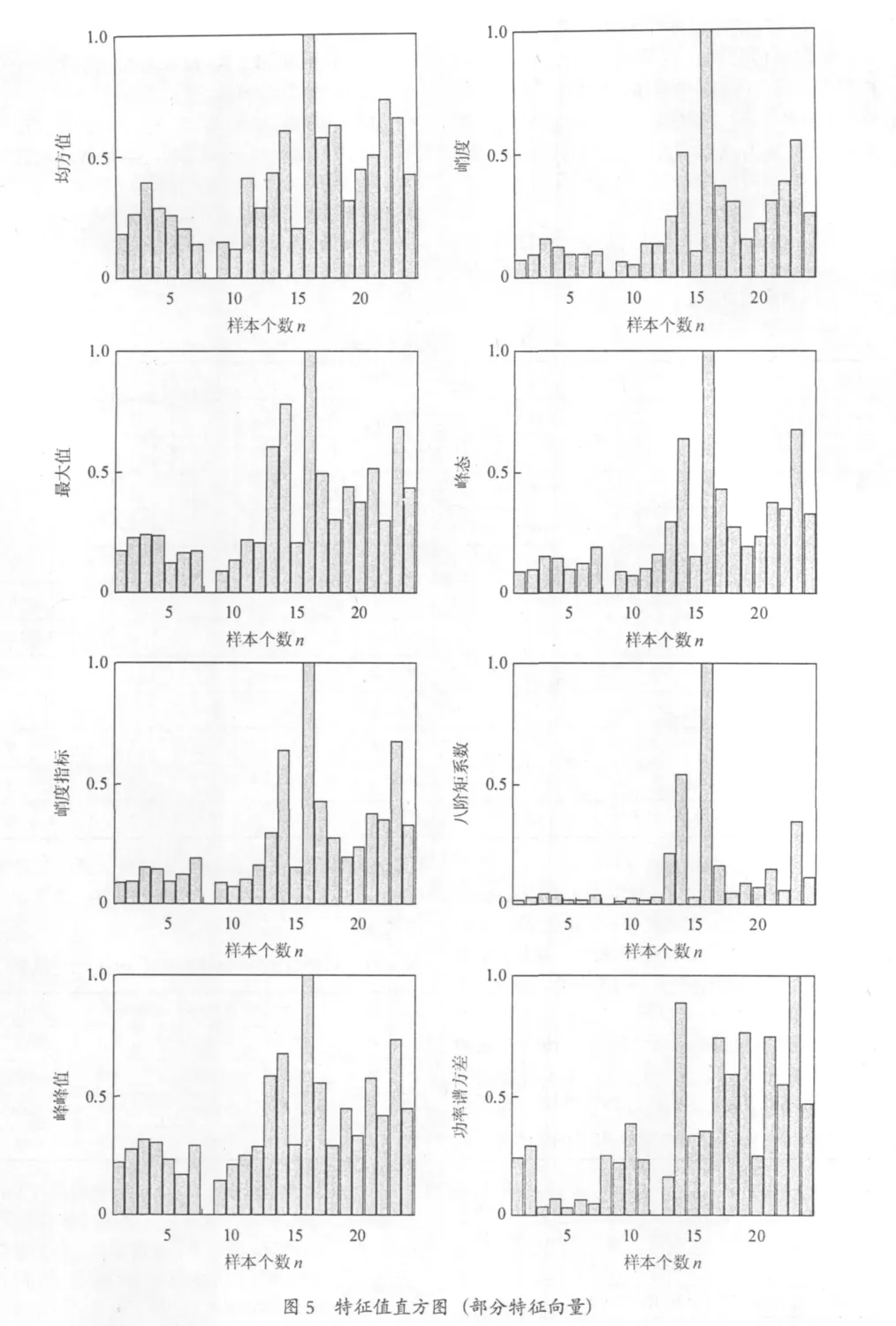
振动信号经过4层的小波包降噪和时域、频域分析后，提取了16个变化较明显的特征值，分别为：均方值，峭度，最大值，峰态，峰值指标，脉冲指标，裕度指标，峭度指标，偏度系数，八阶矩系数，十六阶矩系数，六阶矩，峰峰值，功率谱方差，谐波因子，谱原点矩，用（T1,T2,…,T16）表示。图5表示部分特征值构造的能量直方图，表1为部分特征向量的数值（每种工况3个样本）。

4.2 基于ROSETTA的连续属性离散化

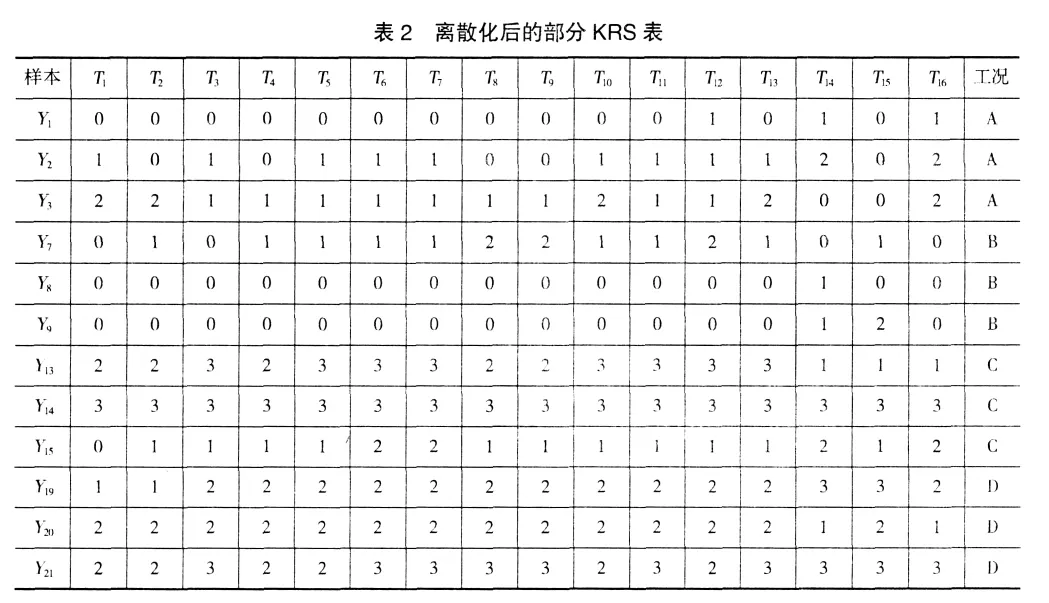
基于ROSETTA软件，采用Semi-NaiveScaler算法将连续的特征值进行离散化，将离散化后的结果进一步量化，部分结果如表2所示，此表是相容的。

4.3 用RS理论进行属性约简和值约简

根据粗糙集理论的不可分辨关系，应用ROSETTA软件约简特征属性。离散后的数据表组成一个数据库K=（U,S），其中论域U为24个样本集，U={Y1,Y2,Y3,…,Y24}，S为小波包消噪、时域、频域分析后构造的特征值，S={T1,T2,…,T16}，根据等价关系：

IND(S)={{8},{9},{1},{10},{7},{15},{5},{6},{2}, {4},{12},{19},{11},{3},{20},{24},{21},{13},{18}, {22},{17},{16},{23},{14}}

所有约简的核为：

CORE(R)=T1,T3,T5,T8,T10,T12,T14,T15

其中的一个约简为：

RED(R)=T1,T3,T4,T5,T8,T10,T12,T13,T14,T15

可见，属性约简后特征向量由16个缩减到10个，分别为均方值、最大值、峰态、峰值指标、峭度指标、八阶矩系数、六阶矩、峰峰值、功率谱方差、谐波因子。然后进行值约简，24个样本约简后的结果如表3所示。

4.4 RBF神经网络故障诊断

如果将构造的特征属性作为RBF的输入向量，输出即为故障模式分类。试验中4种工况的24个样本，每种工况选5个作为训练样本，其余1个为测试样本，经过神经网络的训练和分类，为了便于观察，将输出结果进行归一化处理。未经过ROSETTA软件进行条件属性约简的16个特征向量，其测试样本（C1，C2，C3，C4）的RBF神经网络输出结果如表4所示，经过ROSETTA软件进行条件属性约简后的10个特征向量，其测试样本（R1，R2，R3，R4）的RBF神经网络输出结果如表5所示。

可见未经过粗糙集约简前，第4种故障样本的测试结果，很不理想，比较接近第3种故障类型；而经过粗糙集约简后，各个测试样本的故障类型都能较好的区分出来，诊断的结果更加准确，同时由于减少了神经网络的输入节点数，提高了故障诊断的效率。

5 结论

本文以柴油机缸盖的振动信号为例，以小波包降噪和时域、频域分析后构造的有效特征向量为对象，应用ROSETTA软件进行条件属性的约简，去除冗余信息后，获得了对故障诊断影响最大的几个重要特征向量。用RBF网络对原样本和经属性约简后的样本进行故障分类,结果表明了粗糙集算法对优化特征属性的有效性，经过约简后的特征属性，可以减少神经网络的输入节点数,提高学习效率。

1 Pawlak Z.Rough Sets[J].International Journalof Information and Computer Science,1982,(11): 341-356.

2 SwiniarskiRW,Hargis L.Rough Setsasa FrontEnd ofNeuralNetworks Texture Classifiers[J]. Neurocomputing,2001,36:85-102.

3苗夺谦，李道国.粗糙集理论、算法与应用[M].北京：清华大学出版社，2008.

4程玉胜.ROSETTA实验系统在机器学习中的应用[J].安庆师范学院学报(自然科学版)，2005，11（2）：69-72.

5葛哲学，沙威.小波分析理论MATLABR 2007实现[M].北京：电子工业出版社，2007.

6曹龙汉，曹长修.基于粗糙集理论的柴油机神经网络故障诊断研究[J].内燃机学报，2002，20（4）：357-36.