理想变压器特性方程教学方法讨论

陈希有,刘凤春,董维杰,李冠林

(大连理工大学电气工程与应用电子技术系,辽宁 大连 116023)

理想变压器是电路理论课的必学内容。作为一种理想化的电路元件,理想变压器在建立电路模型、分析电路行为和综合网络函数等研究中发挥重要作用。在“电机与拖动”等后续课程中,变压器是重要内容之一。因此,教学中应使学生透彻理解理想变压器主要特性以及这些特性的电磁学基础和理想化条件等。目前,对理想变压器特性的描述主要有三种典型方式:直接给出定义[1-3］、对线性互感进行理想化[4-6］和对实际变压器进行理想化[7］。本文对比分析了这三种教学方式的特点,详细讨论了理想变压器特性方程在不同导出背景下的理想化假设条件。期望借助此文与读者展开更多交流。

1 用直接定义阐述理想变压器的特性

这种方式类似于定义电阻元件一样直接定义理想变压器特性:满足下列代数关系的二端口元件称为理想变压器,并用图1表示。

式中,n称为理想变压器的变比或电压比,是理想变压器的唯一参数。

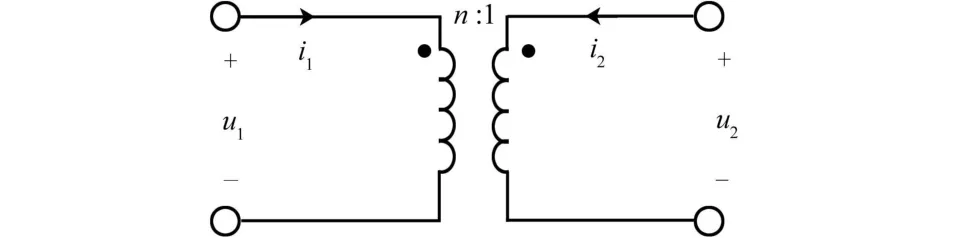
图1 理想变压器的符号

这种教学方式可以直接触及教学要点,在教学时数较少的情况下是一种能够有效节省时间的教学方法。但在教学实践中常会遇到如下质疑:

(1)理想变压器与互感特性完全不同,为什么使用相似的符号?

(2)定义中没有涉及电磁关系,那么如何理解同名端的涵义?

(3)变比等于匝数比,在没有实际变压器做原型的情况下,怎样解释匝数和匝数比?

(4)它既不储能又不耗能的特性只能根据功率的计算结果得出,即

对这种特性的物理机理的解释更是难以讲清,只能强制学生暂时接受。

(5)在理想变压器之前已介绍了理想电阻、理想电感、理想电压源和理想电流源,它们都与实际电阻、实际电感、实际电压源和实际电流源建立了密切的内在联系。相比之下,学生会问到理想变压器与实际变压器存在怎样的内在联系?

采用这种直接定义的方式,教师一时难以回答学生的上述质疑,要待到学习磁路或变压器时才能渐渐解释清楚。

2 对线性互感进行理想化

为避免使用直接定义导致高度抽象的教学弊端,一种可取的方法就是在线性互感模型的基础上做进一步抽象。在讲授互感时已建立了互感的电磁关系,如图2所示,其电路符号如图3所示。

图2 线性互感电磁关系示意图

图3 互感符号

为阐明理想变压器特性方程的假设条件,需简述线性互感特性方程的建立过程。

我们如果忽略介质的涡流损耗,假设耦合线圈周围为线性磁介质,则每个绕组的总磁链等于自感磁链与互感磁链的代数和,这些磁链均与激发它们的绕组电流成正比,即

再忽略导线铜损,并根据磁通的交链关系和电磁感应定律,便得到如下特性方程组:

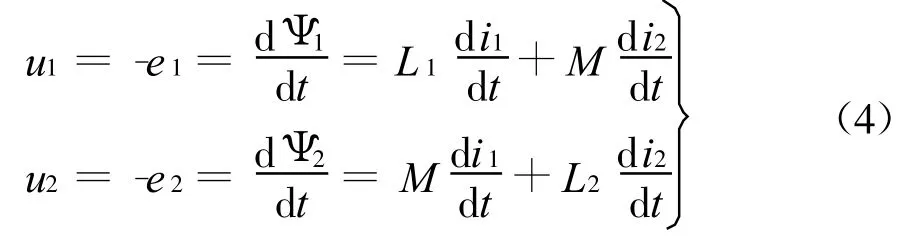
这一关系建立在电磁感应定律基础上,有明确的物理意义。它成立的必要条件是:线性无损磁介质和不计导线铜损。

我们可进一步解释如下:如果存在磁滞损耗,则介质便是非线性介质,磁链与激发它的电流不成正比,总磁链也不能用叠加的方法来计算;如果存在涡流损耗,则式(3)中的磁链还应包含涡流产生的磁链。由于涡流是感应电动势产生的,所以涡流不是与磁链成正比,而是与磁链的时间变化率成正比。故此时总磁链不能仅表达成线圈电流的线性组合,还应包含电流的时间导数,但此时磁链与线圈电流仍属线性关系。

据此推理:对线性磁介质,虽然在直流工作时,满足式(3)的磁链与电流关系,但在交流工作时,如果有涡流损耗,却不满足式(4)的电压与电流关系。

对线性互感进行理想化以便建立理想变压器的过程一般可按如下条件考虑[4］。

理想化条件一:忽略线圈漏磁,即全耦合,耦合系数k=1,互感系数为

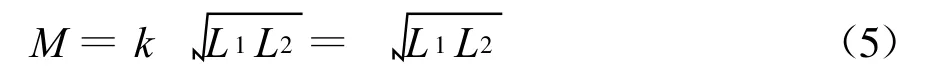
这将导致式(4)中的系数行列式L1L2-M2=0,则两式不再独立,u1和u2必然存在内在联系。为寻此联系,将式(5)代入式(4),可得

比较上述两个电压关系式,便得

再由电感与匝数的平方正比关系,可得

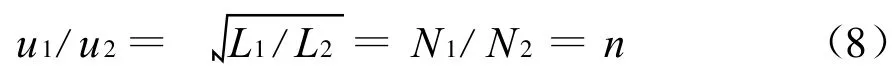
上式便是理想变压器的特性方程之一,即电压变换关系,它表明了u1和u2的内在联系。

由于上述关系是基于线性互感得到的,所以会自然想到,式(8)成立的必要条件应是:线性无损磁介质(磁导率不一定是无限大)、全耦合和无铜损。而事实上,式(8)的成立并不需要满足线性无损磁介质的条件,只需满足全耦合和无铜损条件。这便产生了不一致的结论。见下节分析。

理想化条件二,两自感同比趋于无限大,比值等于匝数比的平方,即

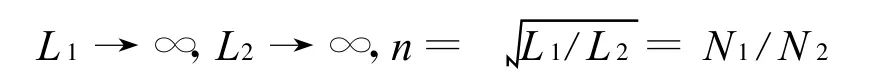
将上述条件代入互感方程(4)得

根据上述方程组中的任意一个方程都可得到

再计算从-∞到t的定积分得

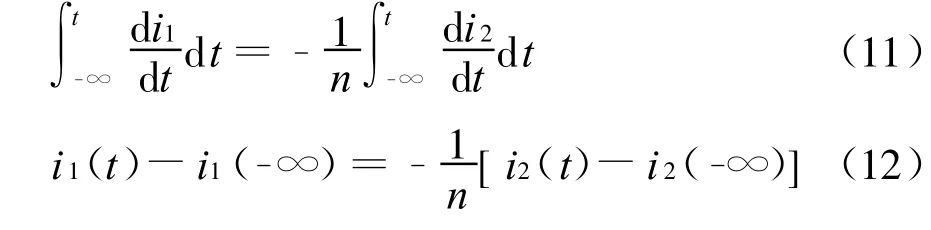
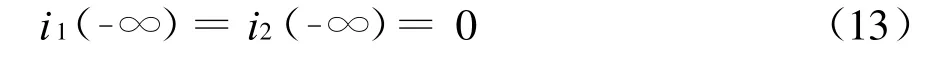
由式(12)和式(13)得到理想变压器的电流变换关系为

式(14)要求自感趋于无限大,在匝数和尺寸一定的条件下,只能是磁导率趋于无限大。亦即自感趋于无限大的假设等同于磁导率趋于无限大的假设,而无限大磁导率的磁介质可视为线性磁介质的一种极端情况。

所以,基于上述对互感的理想化过程得出理想变压器电流变换关系的必要条件是:无损耗、全耦合及磁导率为无限大。

这个条件包括了电压变换所需要的条件,也就是说电流变换所需条件比电压变换所需条件来得更严格一些。故这个条件也就是基于线性互感推理得到的理想变压器的理想化条件。

上述过程将理想变压器建立在线性互感基础上,使理想变压器有了确定的物理原型,并且建立了这两种电磁耦合元件的内在关系。但是从过程上看,仍然不易解释理想变压器为什么不能储存能量?为什么理想化后互感的储能特性消失了?在理想化过程中要保持n,对此也缺少说理性。

3 对实际变压器进行理想化[7］

实际双绕组变压器通常是用良导体做成的两个线圈绕在同一个磁导率很大的铁磁材料即铁心上制成的,如图4所示。

图4 实际变压器电磁关系示意图

由于高导磁材料的存在,线圈电流所激发的磁通主要集中在铁心内部,线圈漏磁通 Υ1σ和Υ2σ相对很小。

1)理想化第一步是忽略线圈漏磁和铜损。这样,每个线圈的磁链 Χ1和 Χ2分别等于其匝数N1和N2与铁心内磁通Υ的乘积,即

2)理想化第二步认为线圈无铜损。这样,各线圈端口电压等于感应电动势的负值,按照图4中的参考方向得

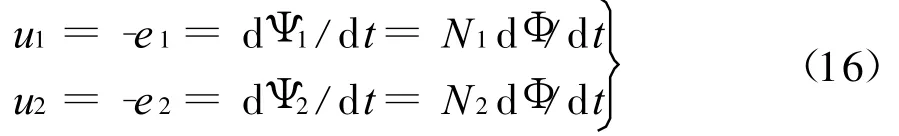
由式(16)便得理想变压器的电压变换关系,即

从上述过程看,电压变换关系成立的必要条件是线圈全耦合和无铜损。对是否存在铁损和介质是否为线性介质没有要求,而从互感推演时,需要线性无损介质。可见,从不同途径推导,需要不同的假设。

3)理想化第三步认为铁心的涡流损耗为零。于是,在图4中沿路径l应用安培环路定律得

需要注意的是:如果存在涡流,则式(18)右边还应包括涡流产生的磁动势,这样便得不到理想变压器的电流变换关系。

4)理想化第四步认为介质磁导率μ※∞,(从而不存在磁滞现象。如果存在磁滞,则磁导率不会始终为无限大)。则铁心内磁场强度为

所以磁场强度沿闭合路径的积分结果为

这样便自然得到理想变压器的电流变换关系为

式(20)清楚表明,电流变换关系成立的必要条件是磁导率μ※∞(不需励磁电流)和不计涡流损耗,它并不需要全耦合和忽略线圈铜损的条件。所以理想变压器的电压变换关系和电流变换关系所需的假设条件是不同的,且二者不存在包含关系。

利用上述电磁原理来理解理想变压器的非储能特性也是很简单的。因为在μ※∞假设下,磁场能量密度变为

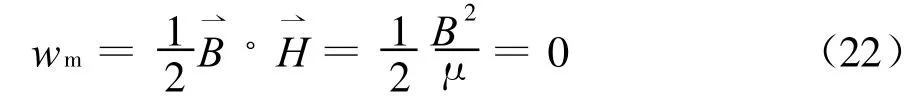
这很好地说明理想变压器虽然存在线圈以及磁感应强度和磁通,但它却是非储能元件。

将电压和电流变换关系合在一起,得到从实际变压器到理想变压器的理想化条件为:无损耗、全耦合及磁导率为无限大。

还需说明,无限大磁导率并不意味着全耦合,全耦合也不一定需要无限大的磁导率。所以,后两个条件是独立的。

第三种教学方法所涉及的电磁学原理,在大学物理课中已经奠定了相应的基础。所以,这种教学方法可以使得不同课程内容之间融汇贯通,能够加深对理想变压器物理背景的理解。也能较好地处理第一种方法中遇到的质疑。不足之处是所需教学时间较长,涉及到的基本概念较多。

4 和磁路教学呼应

对大部分电气工程及其自动化专业的学生来说,在电路理论课中还要学习磁路知识。在学习过程中,严格地建立了图5所示的实际双绕组变压器的相量等效电路,其中含有理想变压器。通过令某些等效参数为零,便可得到理想变压器方程。铜损且绕组为全耦合,则得到理想变压器的电压变换方程。

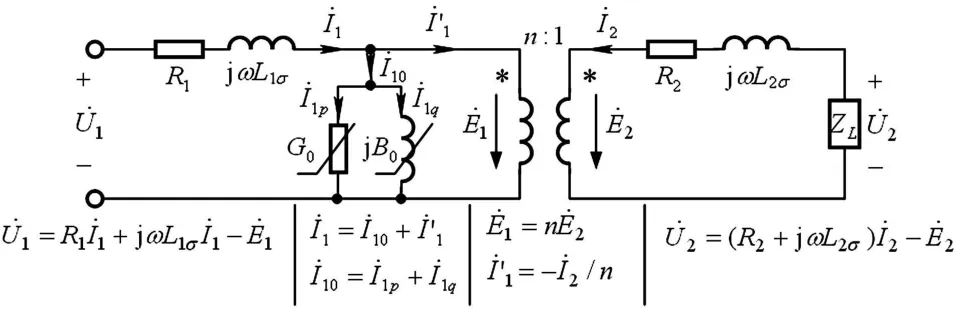
图5 双绕组变压器等效电路

若令G0=0,B0=0,,即不计铁损且磁导率μ为无限大,则得到理想变压器的电流变换方程﹒I1=﹒I2/n 。

这又一次说明了电压变换方程和电流变换方程所需要的假设条件是不一样的。

从上述得到的理想变压器假设条件是:①忽略功率损耗;②全耦合;③磁导率无限大。呼应了第3节的结论。

由于图5是实际变压器的相量模型,所以在上述假设条件下,理想变压器特性方程的相量形式是成立的,在任意时变电压和电流条件下是否还存在这样的变换关系,对此缺少说理性。相比之下,第3节的教学方法却没有这样的质疑,因为第3节的电压变换关系和电流变换关系是在满足假设条件的基础上,基于基本的电磁规律建立的。

5 结语

本文对比分析了时下常用的理想变压器特性方程的三种教学方法及其特点。可根据专业性质、教学时数、教学基本要求及教师个性等选择其一讲授。在后两种方法中,虽然电压变换关系的必要条件不同,电流变换关系的必要条件也不同,但将两个变换关系进行综合,得到理想变压器的必要条件却是一致的。

理想变压器虽然属于经典的电路理论内容,但对其所采取的教学方法仍值得努力探索,愿以此抛砖引玉,并希望得到读者的积极反馈。

本文在成稿过程中,中国工程院院士俞大光对变压器的理想化步骤提出了有益建议;北京航空航天大学雷银照教授对磁介质的性质问题给出了详细解释。他们的基本观点都被作者所采纳。在此,对二位老师的热情帮助表示由衷的谢意。

[1］燕庆明.电路分析教程(第2版),北京:高等教育出版社,2007年6月

[2］陈洪亮,张峰,田舍平.电路基础,北京:高等教育出版社,2007年5月

[3］李瀚荪.电路分析基础(第四版(下册)),北京:高等教育出版社,2006年5月

[4］邱关源.电路(第四版),北京:高等教育出版社,1999年6月

[5］于歆杰,朱桂萍,陆文娟编著.电路原理,北京:清华大学出版社,2007年3月

[6］董维杰,白凤仙.电路分析,北京:科学出版社,2007年8月

[7］陈希有.电路理论基础(第三版),北京:高等教育出版社,2004年1月