钢—混凝土组合梁桥的有限元模型修正

2010-03-20邵新慧

黑龙江交通科技 2010年6期

关键词：匝道桥面模态

邵新慧,李莉,张锐

(1.中航工业北京长城计量测试技术研究所;2.北京市市政工程研究院)

1 工程背景

某立交桥主要由主桥、2号匝道(Z2)和3号匝道(Z3)3部分组成。3座桥均为跨越铁路的大跨度连续梁桥,上述 3桥在Y-16号墩处合并为主桥,Z2、Z3为曲线桥,结构异型,构造复杂。

其中,主桥为 3孔预应力钢—混凝土组合梁结构,其跨径组合为60m+90m+61.45m,桥梁横断面分为3个钢箱,桥梁全宽21.2m。

Z2为 3孔钢—混凝土组合梁结构,跨径组合为 65.37m +97.20m+73.44m,桥梁横断面为单箱单室结构,桥梁全宽8.2m。

Z3为 3孔钢—混凝土组合梁结构,跨径组合 55.04m+ 82.08m+45.91m,桥梁横断面为单箱双室结构,桥梁全宽10.2m。

3座桥结构厚度均为 3.07m,钢箱高度为 2.7m。

该立交桥的下部结构为钢管混凝土圆柱,墩梁固结,基础为钢筋混凝土钻孔灌注桩。

2 理论模态分析

由于该桥结构复杂,Z2、Z3两个匝道桥与主桥结构互相牵制,频率成分密集,即使是通过试验实测也很难分清楚各部分对应的固有频率,因此,本文通过建立的全桥有限元空间模型进行结构的振动特性分析,即理论模态分析,来求出桥梁的固有频率,并以此为依据确定全桥模态试验的测试点布置方案,指导试验模态分析中模态频率的提取。

2.1 有限元分析软件ANSYS简介

本分析采用最为通用和有效的商用有限元软件——ANSYS,它融结构、传热学、流体、电磁、声学和爆破分析于一体,具有极为强大的前后处理及计算分析能力,能够同时模拟结构、热、流体、电磁以及多种物理场间的耦合效应,该有限元计算软件在静动力方面具有速度快、精度高的特点。

2.2 结构简化及有限元建模

初步建立桥梁模型时的主要依据是设计图纸,采用ANSYS有限元结构分析软件对桥梁进行三维立体建模。建模时主要考虑桥面的受力构件,桥梁主体结构的钢箱侧壁板、底板、底板加强筋板和竖向的横隔板均采用SHELL63三维壳体单元构造,根据设计图纸设定不同的厚度。现浇砼桥面板采用SOLID45三维实体单元构造。桥梁下部——钢管混凝土圆柱采用BEAM4空间梁单元构造。对在模态试验中不承力的部件如护栏、沥青混凝土铺装层,建模时不考虑其刚度特性,仅作为改变桥体质量密度的因素,如护栏用LINK8三维杆单元构造,沥青混凝土铺装层没有进行实体建模,仅折算为单位长度的附加质量(线密度),合并到护栏的有限元单元网格中。该立交桥的有限元模型最终为 24713个SOLID45单元,22496个SHELL63单元,10个BEAM4单元和708个LINK8单元,共47627个单元。

桥结构的刚箱部分和桥面现浇砼混凝土部分均按照线性各向同性假设进行建模、计算,其中桥面现浇砼部分由于内部钢筋分布的不均匀性,模型应该按照三维正交各向异性更为合理,但这种建模修正的过程非常复杂,动特性计算时还有可能因矩阵的数值特性不佳而导致结果不收敛,因此在本次计算中即进行了各向同性的工程简化。按照《公路钢筋混凝土及预应力混凝土桥涵设计规范》中对预应力轴心受压构件的正截面强度理论,可计算出等效弹性模量E,公式如下

式中:Ea、Eb分别是素混凝土和非预应力钢筋的弹性模量,而 ∑c则是混凝土达到抗压设计强度时,受压构件中预应力钢筋的应力。而 A、Ab、Ac分别是素混凝土、非预应力钢筋、预应力钢筋的横截面积。

该桥的是钢箱混凝土组合梁,对于桥体以外的基础部分,初步计算时认为它们都是理想刚性条件。主桥与匝道桥交汇一端的边界条件按滑动绞支处理,主桥、匝道桥 Z2、Z3的另一端边界条件都按绞支处理。计算采用的初始常数为:桥面现浇混凝土(50号混凝土)弹性模量3.45×104MPa,密度取 2500kg/m3;桥体钢箱的钢板弹性模量 2.07× 105MPa,密度为ρ=7850kg/m3;钢管混凝土以混凝土和钢材的实际用量计算平均密度值,桥面沥青混凝土铺装层和护栏等桥面其他构造的重量计入护栏的密度中,以考虑其质量对自振特性的影响,目的是保证自振特性计算的正确性。

2.3 理论模态分析及结果

典型的无阻尼模态分析求解的基本方程是经典的特征值问题:

式中:[K]为刚度矩阵;{Φi}为第i阶模态的振型向量(特征向量);ωi为第i阶模态的固有频率(是特征值);[M]为质量矩阵。

对于工程振动问题,只需求解部分特征值。子空间迭代法及Lanczos法等都是针对大型特征值问题的有效解法,不但保证了一定的精度,而且比较经济。Lanczos法虽跟子空间迭代法类似,都是向量反迭代法和R-R法相结合,但它结合得更巧妙,通过矢量块进行Lanczos递归运算,使计算过程大大简化,对同样的问题,它和子空间法具有相同的精度,但它比子空间迭代法快 5～10倍,是一种计算效率更高的求解法。本分析中桥梁模型自由度数很大,在进行模态提取时选用分块Lanczos算法,计算得出的该桥前6阶固有频率,列于表1。

3 试验模态分析

立交桥的试验模态测试,采用天然脉动作为激励的环境随机振动的测试方法。根据理论模态分析结果,确定了分别对主桥、Z2和Z3匝道桥进行测试的方案,图 1为模态试验测试布点图,由于要考察匝道桥扭转振动情况,所以在桥面两侧都布置了测点。

通过试验获得三组模态测试数据,对这三组数据采用复指数法(PRONY)进行模态参数辨识(OMA)。由于主桥、Z2和 Z3匝道桥三部分在一端有联系,所以所有模态频率在这三组数据中都会出现,且相互影响牵制。为了在如此密集的模态参数中辨识出各阶频率来,还需要参考有限元模型的理论计算结果,比照各部分测试数据的模态特征,区分出各部分的模态频率和模态振型,最终识别出了主桥、Z2和 Z3匝道桥的总前六阶模态频率,见表 1。

图1 模态试验测点布置图

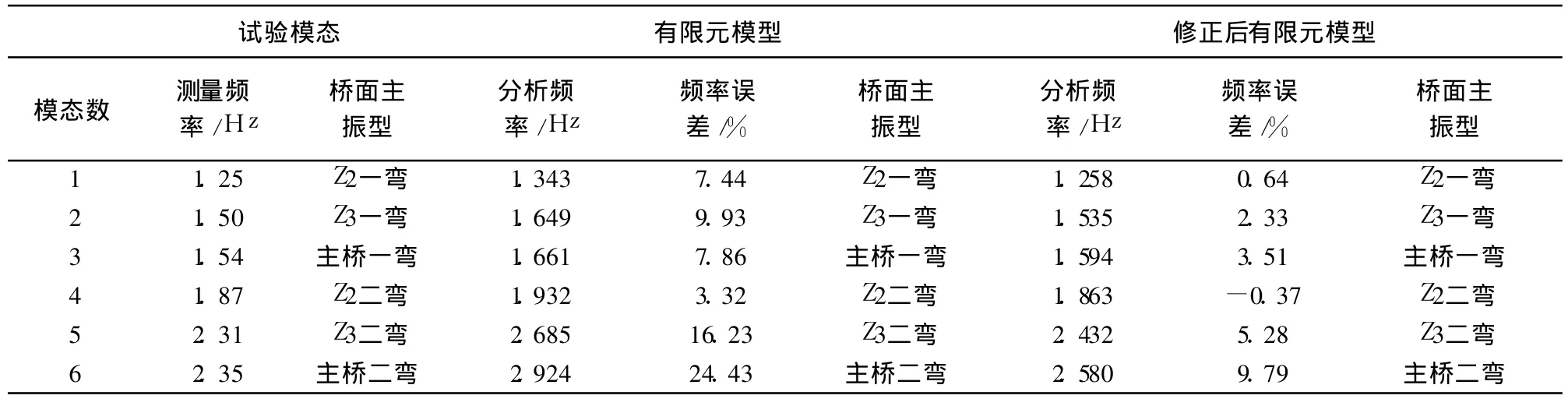
表1 有限元模型修改前后理论模态分析与试验模态分析的对比

4 结果对比及有限元模型修正

桥梁的空间有限元模拟计算是建立在一定的假设理论基础上的,有限元模型也是经过简化处理的,而且桥梁在施工时与图纸会有一定的误差,所以理论计算得到的结果与试验模态分析结果之间有一定的误差,频率误差结果见表 1。

由于模型庞大、复杂,参数修正主要采用手工完成。模型的修改主要集中在桥面现浇砼钢筋混凝土材料的弹性模量确定,修正依据是测试时桥梁的外观检查数据和材料属性测试数据。修正后模型的弹性模量较初始建模时一般都有所变化,这是合理的,主要是由于实际结构具有各种缺陷如施工缺陷、裂纹的等,导致弹性模量值比理论值要小。另外根据桥梁的外观检查情况和现场施工进度,修改模型的尺寸以及护栏和沥青混凝土铺装层的合成参数,使之与实测情况相吻合。修正后的理论模态分析结果见表 1,各阶理论模态振型与试验模态振型的比较见图 2。