钢筋混凝土深梁极限荷载的计算方法

吉红梅

(黑龙江省公路勘察设计院)

1 塑性理论极限分析的方法

在钢筋混凝土的塑性理论中,常用上限定理求解结构或构件的极限荷载。

上限定理指的是在所有与机构的容许位移场对应的任何荷载均大于或等于极限荷载。由上限定理可知:对于一个给定的结构与荷载系,当它按某一形式破坏时,即存在着内力功不比外力功大的变形状态,由于此时结构已经破坏,则根据功能等式求出的荷载值总是大于或等于真正的极限荷载,此荷载为极限荷载的上限。根据极限分析的上限定理求解极限荷载的方法即为上限方法。

上限方法是以上限定理为依据,其基本思想是:从平衡条件和机构条件出发,寻出一个能满足塑性条件的内力状态,最后运用虚功原理确定极限荷载。在上限方法中,一般先假定一个破坏机构,并使外力在假设的破坏机构上做正功,然后利用内力功与外力功相等的原理求出与破坏机构对应的极限荷载。由此所得的数值一般不会小于正式的极限荷载,在这种情况下,应该选取有限个数值中最小的一个,因为它是最接近实际破坏时的荷载。

具体研究方法是:假定钢筋和混凝土均是刚塑性材料,认为结构破坏时形成一个机动体系,该体系由若干个刚性区组合而成,各个刚性区之间以塑性铰线相连,然后以外荷载所做的功等于结构或构件内部所耗的塑性内功的原理,建立塑性方程,求出破坏荷载。通过大量试验得出的实验数据和用运用这种理论求解钢筋混凝土深梁抗剪强度的结果进行比较和数值分析,从而研究出一种可靠而简便的求解钢筋混凝土简支深梁抗剪强度的计算方法。

2 材料的塑性性质

2.1 混凝土的应力

钢筋混凝土深梁的腹板处于一种平面应力状态。在计算中,混凝土的单轴抗压强度 fc与实测的圆柱体抗压强度f′c之间的关系用一个有效系数v表示

式中:v为混凝土的有效系数;

当混凝土处于双向受压的状态时,屈服函数f1=-fc-σ1和f2=-fc-σ2成立。如果忽略混凝土的抗拉强度,则f3=σ1和f4=σ2也成立,对应的混凝土主应力屈服轨迹如图 1所示,这就是众所周知的四方形屈服轨迹或库仑破坏准则。

图1 混凝土平面应力的四方屈服轨迹

图1中,有 4个屈服函数,它们是

式中;σ1,σ2为混凝土平面应力中的正应力(MPa),以拉为正。

由公式(2)可知,钢筋混凝土深梁中的主应力如下

2.2 钢筋的应力

钢筋被认为是一种理想的塑性材料。假定在拉力和压力作用下,钢筋的屈服强度是一样的。那么钢筋特有的理想化的塑性 σ-ε关系曲线如图 2所示。

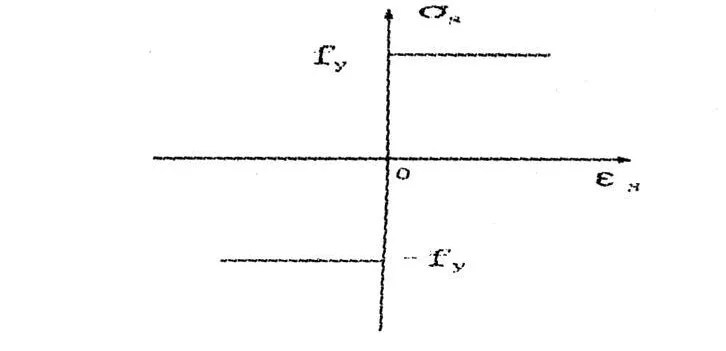
图2 理想刚塑性钢筋的应力—应变关系

式中:fy为钢筋的屈服强度,MPa;σs为钢筋的应力,MPa。

2.3 混凝土的应变及钢筋的位移

钢筋混凝土深梁的位移计算模型如图 3所示。当深梁发生剪切破坏时,屈服线 AB把梁体分隔成块体Ⅰ和块体Ⅱ。(屈服线一般有 3种形状:抛物线型、直线型和折线型。对钢筋混凝土简支深梁而言,屈服线的形状由瞬时转动中心的位置决定。如果瞬时转动中心位于以 AB为直径的圆圈以外,最佳的屈服线线形是抛物线;如果如果瞬时转动中心位于圆圈内或圆上,屈服线的线形是折线型;当瞬时转动中心位于无穷远的位置,屈服线的线形是直线型。)假设在屈服线上的变形均匀,其厚度为Δ。两个刚性块体的相对位移是 δ,与屈服线的倾角是α。两个刚性块体在平面绕瞬时转动中心O′旋转。在总体坐标系X-Y中,块体Ⅰ可能产生 3个位移:水平位移 U1,竖向位移V1和转角 Ω1。块体Ⅱ也有3个位移,U2,V2和 Ω2。

图3 深梁的计算模型

在屈服线两边相对于瞬时转动中心的相对位移如下

瞬时转动中心相对转角O′的坐标(XRC,YRC)可由下式给出

因为屈服线的变形不连续,而混凝土和钢筋都是处于塑性状态,所以钢筋和混凝土的应变不能从弹性方法确定。

(1)混凝土的应变。

如图 4所示,取出屈服线的一小部分,Δ表示两个刚性块体Ⅰ和块体Ⅱ之间的窄屈服区域的宽度,t方向是屈服线的切线方向,n方向是屈服线的法线方向,两个刚性块体的相对位移是δ,其与屈服线的夹角是α。

图4 两个刚性块体之间的变形

可推导出混凝土平面应力中的主应变为:

(2)钢筋的位移。

如图 5所示,当通过屈服线的钢筋达到屈服强度时,即钢筋中的应力等于 fy时,它通过屈服线的塑性位移可由公式(8)计算。

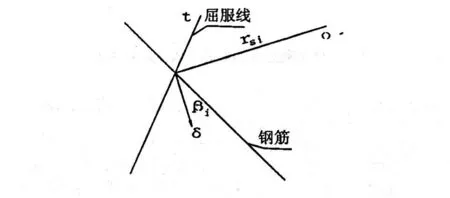
图5 钢筋的位移模型

式中:β为位移方向和钢筋之间的夹角;rsi为钢筋与屈服线的交点和瞬时转动中心之间的距离,mm;

在剪切破坏状态中,屈服线上钢筋的拉力可用公式(9)计算

式中:Ts为屈服线上钢筋的拉力,N;As为屈服线上钢筋的面积,mm2。

3 材料内部的耗散能量和外力功

当钢筋混凝土深梁处于破坏状态时,一般把深梁看成一个刚性构件。构件被屈服线互相分隔。如果用 NYL表示屈服线,那么在破坏机构的模型上,钢筋和混凝土的全部耗散能量(即内能损失或内力功)WI如下

公式中的Wc和Ws分别是指的在屈服线上混凝土和钢筋的耗散能量。它们由下面方法确定。

3.1 混凝土的耗散能量

(1)屈服线是直线型。

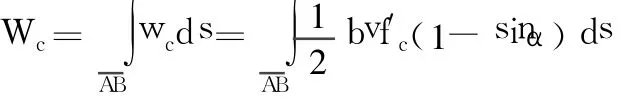
公式(11)也适用于屈服线是抛物线型。

(2)屈服线是折线型。

在公式(11)和公式(12)中:

式中:Lc为直线型屈服线的长度或抛物线型屈服线的弦长, mm;rm为屈服线中点m和瞬时转动中心之间的距离,mm; αm为位移δm与直线型屈服线或抛物线型的弦线在中点位置的夹角;l为双直线型屈服线上的受压区长度,mm。

其他符号与前面一致。

3.2 钢筋的耗散能量

如图5所示,假设一个纵筋与屈服线相交,与位移δ成β角,而且所有钢筋的强度都是fy, 则纵筋的耗散能量是

那么,所有钢筋(指横向、竖向和纵筋钢筋)的全部耗散能量是

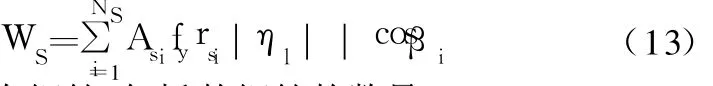
式中:Ns为指所有钢筋,包括的钢筋的数量。

3.3 外力功

假设在梁上作用一力系(荷载系)Pi(i=1,2,3…),这些力是按比例同时增加的。则外载做的外功WE由下式确定

式中:NP为结构模型上荷载的数量;Pi为结构模型上的荷载,N;δi为荷载Pi产生的位移;λ为荷载系数。

4 利用塑性理论上限方法求极限荷载

根据能量守恒的基本原理,有

根据(15)式可以推导出关于荷载系数 λ的表达式。可以看出荷载系数 λ是与 U,V,Ω等材料强度以及构件尺寸有关的系数,则λ可用含有少许变量的隐函数表示

其中:U,V,Ω为结构模型的刚性位移;fm为材料强度;Gm为材料的几何性质。

无量纲荷载系数 λ可以表示为公式(17)的形式

采用数值优化的方法,对上述公式(16)求极小值,即可得到上限方法的最小值λ,再由公式(17)即可求出塑性条件下剪切破坏的破坏荷载P。

一般对结构或构件进行弹性和塑性分析时,随着荷载由零逐渐加大,最终都可获得结构或构件的极限荷载值及对应的塑性机构,这种方法是系统的、具体的、程式化的,它不但可以求出极限荷载,而且可以建立结构在变成塑性机构之前的每个阶段中荷载和变形的明确关系。但是,这种方法往往是很繁琐的,甚至是极其困难的。因此,当我们实际上只对极限荷载感兴趣,而对结构在变成塑性机构前的变形无需考虑时,则可避开破坏前的全部分析,直接计算破坏荷载。这样在计算上就大大简化了。利用塑性理论极限分析的基本原理,用简单的数学运算对钢筋混凝土深梁进行塑性极限状态分析,避开破坏前的过程分析,只计算钢筋混凝土深梁的极限荷载。如果用塑性理论分析得到的结果,与由弹性状态到弹塑性状态再到塑性极限状态进行分析的结果完全一致,则这种方法将是一种可靠而简便的方法,这个理论也是切实可行的。

[1] A.K.H.Kwan,XiLinLu,Y.K.Cheung.ElasticAnalysisofSlitted Shearwalls.JournalofStructure,1998.

[2] 斯图亚特S.J.莫易著,陈维纯,马宝华译.钢结构与混凝土结构塑性设计法,1986.

[3] F.K.Kong.ReinforcedConcreteDeepBeams.BlackieSonLtd. GlasgowandLondon,1990.

[4] 徐秉业,刘信声.结构塑性极限分析[M].中国建筑工业出版社,1985.