军都山斜拉渡槽索力测试

李召娟

(河北道桥工程检测有限公司)

军都山斜拉渡槽是北京市延庆县白河堡水库南干渠上的重要输水建筑物。该渡槽是一座跨度为 66m+126m+ 66m的双塔双索面悬浮式混凝土斜拉渡槽,是我国目前最大跨度和流量的斜拉渡槽,其宽跨比仅为 1/39.375,是世界上宽跨比最小的斜拉钢筋混凝土结构之一。该渡槽结构采用扇形密索、四柱框架式塔墩、U形断面主梁(即槽身)、三孔连续的塔墩固结悬浮体系。该地区为山口地带,冬春季多风,最大风速达24m/s。

每塔 10对斜拉索和垂直索组成一个索面。全桥共 84根拉索,其中外边索与槽身最小夹角21°,最大索长 65.1m。每根索根据拉力大小分别采用 4、6、8根Φ15(7Φ5)钢绞线,两端用组合式槽销锚锚固在索塔和槽身牛腿上。拉索外套PE管,采用内灌水泥改性浆的方法进行拉索防护。

1 现有的一些索力测试方法

斜拉索是斜拉渡槽、塔和索体系中的一个重要组成部分,斜拉索索力大小直接影响渡槽上部结构的受力和变形状态。渡槽在使用过程中,拉索往往由于腐蚀和振动等原因受到损害,导致拉索的索力松弛,而变化的索力会影响结构内力分布和结构线型,因此索力可以作为结构健康状态评估的重要指标。

目前,索力测定的方法有以下几种。

(1)压力表测定法。由于千斤顶的张拉油缸中液压和张拉力有直接的关系,所以测定张拉油缸的液压,就可求得索力。压力表测定法是施工过程中控制索力最常用的一种方法,但它无法测量已张拉完毕的拉索。

(2)压力传感器测定法。张拉时,在千斤顶张拉活塞与连接杆螺母之间套装一个穿心式的压力传感器,受压后输出电讯号,于是就可在配套的二次仪表上读出千斤顶的张拉力。压力传感器的售价相当高,尤其是大吨位的传感器就更贵,自身重量也大。因此只在特定场合下使用。

(3)其他方法。包括电阻应变片测定法、拉索伸长量测定法和索拉力垂度关系测定法。这三种方法从理论上讲是可行的,但实施会遇到较多的实际问题,一般不予采用。

由以上分析可知,现有的这些直接测定索力的方法,或者不尽合适,或者无法复测索力。

2 振动法测索力及存在的一些问题

振动法也称为频率法,即实测斜拉索的固有频率,利用索的张力和固有频率的关系计算索力。振动法可采用激振器激振或人工激振,亦可采用环境随机振动法。测试时用索夹或绑带将传感器固定在拉索上,以环境振动或者强迫激励拉索,传感器记录下时程数据,并由此识别出索的振动频率。

振动法测定索力,设备可重复使用,整套仪器携带、安装方便,测定结果可靠。当需要对已施工完毕的斜拉索的索力进行复测时,频率法几乎是惟一的选择。

采用基于振动理论的频率法,其索力测量精度受到很多因素的影响,下面列出主要的影响因素并寻求出解决的办法。

(1)实际的拉索具有一定的抗弯刚度。

将拉索的抗弯刚度考虑进弦振动理论,其微元的动力平衡微分方程为

式中:y为横向坐标(垂直于拉索的长度方向);X为纵向坐标(沿拉索的长度方向);m为单位索重;T为拉索的索力;t为时间;EI为拉索的抗弯刚度。

当拉索两端的边界条件铰支时,上述微分方程的解可以表示拉索索力的显示解

式中:T、m、EI同上;l为拉索的长度,m;fn为拉索的第n阶振动频率,Hz;n为拉索的振动阶次。

(2)实际的拉索由于自重具有一定的垂度。

面内对称振动使有一定垂度的索伸长,因而产生附加的拉力,从而对面内对称振动产生影响。而面外振动不会引起索的伸长,因而索的垂度对索的面外自振频率没有任何影响。现场测试时,如将加速度传感器侧向捆绑,则可采集到面外振动的数据。从而所测索的自振频率不受索的垂度的影响。

(3)拉索的边界条件(计算长度)的影响。

斜拉索一般采用 Φ5或 Φ7的预应力高强钢丝并拢经大节距扭绞而形成的半平行钢丝索。从实验得知,扭绞角小于4°时,其弹性模量和疲劳性能不受损减。斜拉索两端为冷铸墩头锚。这种拉索既非理想的柔性索,两端也不完全是固定铰接。对于理论模型与实际拉索边界条件的差别可以用修正索长的办法进行模拟,即用于索力计算的计算索长 L的取值要比拉索两端的实际锚固点间距小。经过大量的数据分析整理得出,索长修正的经验公式为

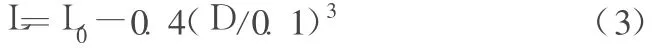
式中:L为斜拉索的计算索长;L0为斜拉索上下两端索孔锚板中心的几何距离;D为斜拉索外径。

3 用振动法对军都山渡槽斜拉索进行索力测试

测量时不必对被测的拉索进行人为激振。由于风等环境随机振动的激励,拉索一直在作微幅的随机振动。加速度传感器将拉索的这种随机振动信号转变成电信号,电信号经放大器放大后送到信号分析仪或带有信号分析软件的计算机中进行谱分析,便能确定被测拉索的振动频率。

自振特性的测量及分析仪器采用加速度传感器配滤波放大器和便携式数据采集分析仪,具体型号及配套框图如下:

图1 斜拉索索力测试流程图

本次数据采集采用北京东方振动和噪声技术研究所的INV306型智能信号采集分析系统。测量斜拉索索力的基本步骤:

(1)将加速度传感器用索夹或绑带侧向固定在索上人手可及的高度;

(2)测量并记录各测点水平方向的面外振动信号;

(3)对测得的各点响应信号进行谱分析处理,得到各测点响应信号的功率谱;

(4)各阶模态的自振频率可以通过谱图上的峰值位置来确定;

(5)根据拉索的索力与其自振频率存在的关系推算出该拉索的索力。

图2为一测点的典型的环境振动加速度时程曲线,对采集到的环境振动加速度进行自功率谱分析,即可得到图 3典型的振动功率谱曲线。将拉索的抗弯刚度、索长、单位索重及索两端的支承条件等参数输入分析系统,即可得出拉索的索力。当然,也可以利用公式(2)自己算出。

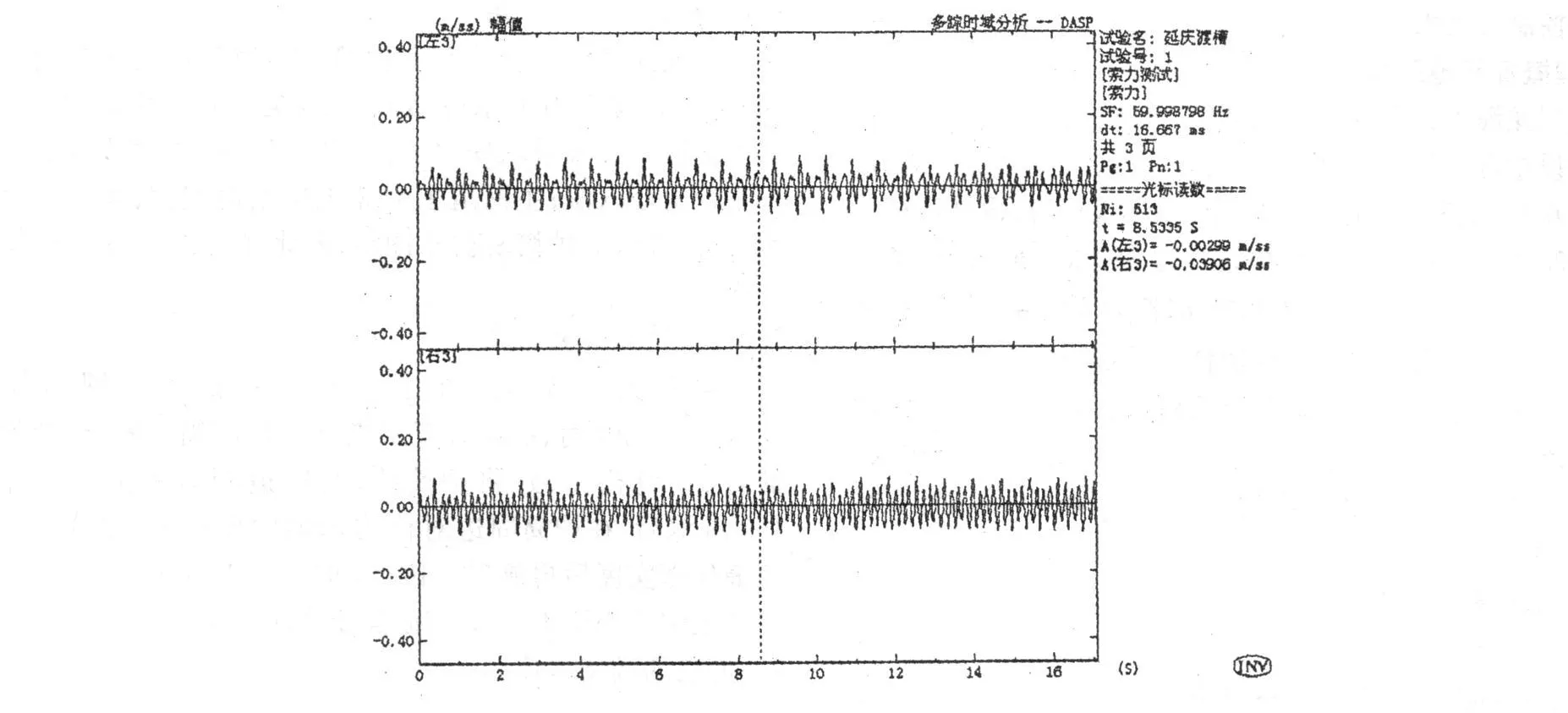
图2 典型的斜拉索环境振动加速度时程曲线(3号斜拉索)

图3 典型的振动功率谱曲线(3号斜拉索)

图4 典型的斜拉索索力曲线图(3号斜拉索)

通过对军都山斜拉渡槽 84根斜拉索频率的现场测试,即可得出每根拉索的索力值。

实测过程中存在以下一些问题。

(1)由于一阶振型在索中央处振幅较大,在端部振幅很小,实测中受条件限制,传感器只能安装在拉索靠近桥面端附近,因而一般得到的信号中基频成份就相对较小,而高次谐波成份占优势。由弦理论公式可知,当索力一定时,高阶频率是基频的整数倍,表现在功率谱上则是谱上会出现一系列等间距的峰值,峰值的间距就是基频。由此我们可以判断出各峰值对应的为几阶频率。

(2)对于环境随机振动测试,由于干扰因素较多,所以采样时间要适当加长。一般可设为600s。

[1] 刘士林.梁智涛等.斜拉桥[M].北京:人民交通出版社, 2002.

[2] 王卫峰,韩大建.斜拉桥的索力测试及其参数识别[J].华南理工大学学报,2001,29(1):18-21.

[3] 杨佑发,白文轩,魏建东.采用Ernst公式计算斜拉桥拉索振动特性的精度分析[J].世界地震工程,2008,24(2):50-53.