可信网络匿名连接方案

庄俊玺,公 备

(北京工业大学计算机学院,北京 100124)

可信网络匿名连接方案

庄俊玺,公 备

(北京工业大学计算机学院,北京 100124)

在开放式网络连接环境中,可信网络终端在进行身份证明时不希望暴露自己的身份,本文提出了一种基于环签名的可信网络连接客户端匿名认证方案,引入环管理员机制以保证环成员都是合法的可信网络连接客户端,本方案的安全性基于CDH假设和强单向函数,且参数较短,易于实现.

环签名;双线性映射;强单向函数;CDH假设

国际上可信计算联盟(TCG)提出了基于可信计算的可信网络连接架构(TNC)[1],它通过提供一个由多种协议规范组成的框架来实现一套网络接入标准.

国内在沈昌祥院士的主导下,提出了采用三元对等鉴别协议的网络访问层,利用该协议实现终端和策略执行点的双向身份认证.

在开放式网络连接环境中,可信网络终端在进行身份证明时不希望暴露自己的身份,仅使网络接入端知道自己是一个合法用户即可,因此,本文提出了网络匿名连接方案,不仅保证接入的终端是合法的同时保证连接的匿名性.对于匿名连接方案,TCG提出了可信平台控制模块的直接匿名证明方案(DAA),DAA方案基于Camenisch-Lysysanskaya群签名[2-6],通过向第三方证明自己的身份得到信任证书,再通过证书产生签名向验证者证明自己的身份.但是DAA的证明过程过于繁琐,计算过程过于复杂,本文提出了基于环签名的证明方案.传统的环签名没有认证中心,虽然可以保证匿名性,但是不能保证安全性.本文的环签名方案加入了一个环管理者,这样既可以实现匿名证明又可以防止无赖的可信网络终端,从而保证了匿名性和安全性.

1 预备知识

1.1 环签名

由Rivest等[7]在2001年提出,它能实现签名者无条件匿名的签名,环签名的构成算法分为3种.

1)密钥生成算法Gen 环签名的密钥生成算法都是概率多项式时间复杂度(PPT)的算法,当给出安全参数即密钥长度,由密钥生成算法生成私有密钥和公开密钥.

2)签名算法Sign 环签名的签名算法也是概率多项式时间复杂度的算法(PPT),当输入消息m和n个环成员的公开密钥{PK1,PK2,…,PKn}以及其中的一个成员的私钥SK后,对消息m产生一个签名 σ,其中签名 σ中的某个参数根据一定的规则呈环状.

3)验证算法Verify 确定性算法,输入(m,σ)后,若 σ为m的环签名则输出“True”,否则为“False”.

1.2 基本概念

定义1 双线性映射 下设群G1=〈g1〉和群 G2=〈g2〉是2个q阶循环群,q是一个大素数,群G1和G2之间存在同构映射记做g1=φ(g2)(其中 φ是群G1和群G2之间的同构映射),而且满足

1)可计算的双线性 存在可计算的映射e∶G1×G2→G3(G3也是一个阶为q的循环群)使得任意的η∈G1,γ∈G2,都存在 e(ηa,γb)=e(η,γ)ab.

2)非退化性 对于任意的群上的非零元 η∈G1,γ∈G2,e(η,γ)≠1.

定义2 计算性Diffie-Hellman假设 对于给定的安全参数k,g是符合安全参数的长度群G的一个元素,给定(g,ga,gb)∈G,a,b是秘密参数,a,b∈Zp,p为素数,那么对于不知道a,b的情形下计算gab,在多项式时间内是不可行的.

定义3[8]强单向函数 如果一个函数f∶{0,1}*→{0,1}*满足

1)易于计算 存在一个确定性的多项式算法A,使得输入为x时,算法A的输出为f(x),亦即A(x)=f(x).

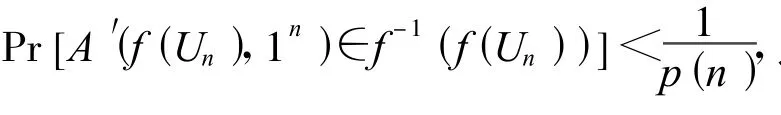
2 可信网络连接匿名认证方案

本方案增加一个环管理员与群管理员,不同的是环管理员只验证成员的合法性,不打开签名的权限,从而保证了签名的匿名性.选定一个阶为素数p的群G,以及整环Zp,G为以g为生成元的乘法循环群,GT为以g′为生成元的乘法循环群,定义2个散列函数Hid∶{0,1}lid→G,Hm∶{0,1}lm→Zp(Hid和Hm均为无碰撞的强单向函数),选择g1=gx(x∈Zp),g2∈G,定义e∶G×G→GT为从G到GT的双线性映射,整个系统的公开参数为(G,GT,e,p,g,g1,g2,Hid,Hm).

2.1 环成员的加入

环签名的成员不能是无赖的可信网络连接终端.对每个可信网络连接终端的IDi做 γi=Hid(IDi),生成一个序列 R={γ1,γ2,…,γn}.

可信网络连接终端向环管理员证明自己的合法性,同时生成自己的签名密钥.

2)可信网络连接终端用AIK私有密钥解密nc,选择ra,rb∈Zp,计算,然后,将可信网络连接终端将计算结果 (v1,v2,σa,σb,Ra,Rb,v3,σ′)发送给环管理员.

3)环管理员首先验证v3是否与无赖可信网络连接终端列表中的某个值匹配,如果匹配则拒绝可信网络连接终端的加入申请,否则验证是否成立,如果成立则说明可信网络连接终端拥有正确的AIK私钥,并且这个可信网络连接终端是合法的可信网络连接终端.

4)环管理员使用AIK的公开密钥加密每个v′∈Zp给申请加入的环成员.

2.2 签名过程

1)当通过环管理员验证之后,申请加入的可信网络连接终端成为第i个环成员,其收到v′之后计算v=v′+x1+x2.

2)对消息M进行签名,计算m=Hm(M),环成员计算其私钥di=(g2xγiv,gv).

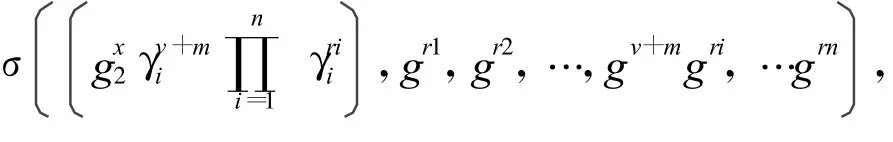
2.3 验证过程

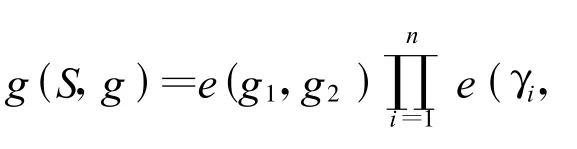
3 安全性分析

3.1 正确性

根据双线性群的性质,可以推导出

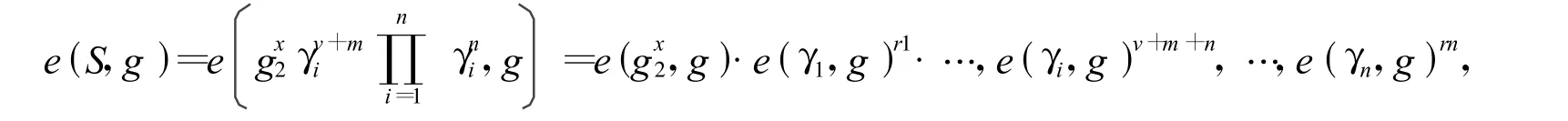
根据双线性映射的性质,可得

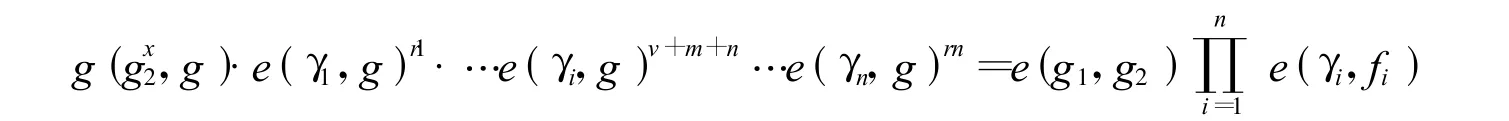
从而得出签名和验证方案正确.

3.2 无条件匿名性

定理1 可信平台控制模块在申请成为环成员过程中是匿名的.

证明:因为 γi=Hid(IDi),所以,可信网络连接终端向环管理员认证阶段的匿名性取决于Hid∶{0,1}lid→G的强度,由于Hid∶{0,1}lid→G是强单向函数,设A′(Hid(IDi))为求逆算法,则有

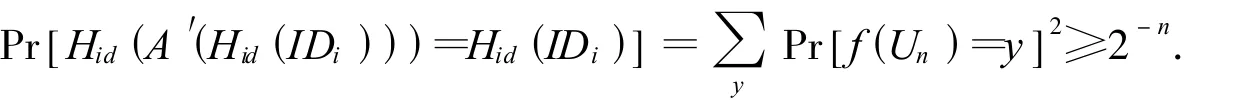
2)设A′(Hid(IDi))是固定输出算法,对于给定 γi=Hid(IDi),A′(Hid(IDi))都输出固定的序列,因此固定输出算法A′的求逆概率为

由此可知,单向函数求逆的概率最差为2-n,所以对于强单向函数 γi=Hid(IDi),求逆的概率满足

那么,γi=Hid(IDi)求逆的概率为2-n≤Pr[A′(Hid(IDi))]＜1/p(n),因此,如果想知道可信网络连接终端的身份信息,几乎等同于暴力破解,所以,可信网络连接终端在申请成为环成员的过程中是匿名的.

定理1得证.

定理2 可信平台控制模块在签名过程中是匿名的.

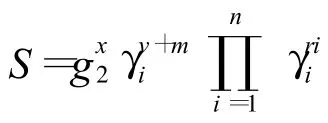
定理2得证.

3.3 签名不可伪造

只有合法的环成员才能通过环管理员的验证,才能收到v′,才可以计算v=v′+x1+x2,进而生成签名密钥本文提出的签名方案是基于CDH假设的,在多项式时间内从 σ=(S,f1,f2,…,fn)签名中不能得到签名密钥的任何信息,从工程角度来看,签名在有效时间内是不可伪造的.

4 结论

本文提出的可信网络匿名身份认证方案的安全性基于强单向函数及CDH假设,该方案满足正确性、匿名性,以及签名不可伪造,本文提出的认证方案是安全的,而且该方案有着较短的参数,效率较高,易于实现.

[1]Trusted Computing Group.TCGTNC Arthitecture for Interoperability Specification Version 1.3[S].Released 6 Phoniex:TCG Published,2008.7.

[2]CAMENISCH J,STADLER M.Efficient group signature schemes for large groups[C]∥Advances in Cryp tology-CRYPTO'97,California:Springer Verlag,1997:410-424.

[3]CAMENISCH J,MICHELS M.A group signature scheme with im proved efficiency[C]∥Pei,editors,Advances in Cryptology-ASIACRYPT'98.Beijing:Springer-Verlag,1998:160-174.

[4]CAMENISCH J,MICHELSM.Separability and efficiency for generic group signature schemes[C]∥Advances in Cryptology-CRYPTO'99 California:Springer-Verlag,1999:413-430.

[5]CAMENISCH J,LYSYANSKAYSA.Dynam ic accumulators and application to efficient revocation of anonymous credentials[C]∥Advances in Cryptology-CRYPTO 2002,California:Springer-Verlag,2002:61-76.

[6]CAMENISCH J,LYSYANSKAYA A.A signature scheme with efficient protocols[C]∥Security in Communication Networks,Third InternationalConference,SCN 2002 Berlin,New York:Springer-Verlag,2003:268-289.

[7]RIVEST R L,SHAMIRA,TAUMAN Y.How to leak a secret[C]∥In Asia Crypt2001.Berlin:Springer-Verlag,2001:552-565.

[8]GOLDREICH O.Foundations of Cryptography[M].London:Cambridge University Press,2001:35-36.

(责任编辑 张士瑛)

The Connection Anonymous Scheme of Trusted Network

ZHUANG Jun-xi,GONG Bei
(College of Computer Science,Beijing University of Technology,Beijing 100124,China)

In an open network access environment,the trusted network clients do not want to expose their identity.In this paper a new trusted network connection anonymous authentication scheme is presented,which is based on ring signature.By adding a ring administrator,it can be ensure the members of the ring to be the legitimate trusted network clients.The safety of the scheme is based on the CDH assumption and strong one-way function.It is suitable for engineering because of shorter public parameter size.

ring signature;bilinearmap;strong one-way function;CDH assumption

TP309

A

0254-0037(2010)05-0597-04

2009-12-10.

国家“八六三”计划基金项目资助(2006AA01Z440,2009AA012437);国家 “九七三”计划项目资助(2007CB311100);核安全与仿真技术国防重点学科实验室开放课题基金资助(HEUFN0801).

庄俊玺(1981—),女,河南新乡人,讲师.