Terahertz波参量振荡器辐射THz波的理论研究
2010-03-19苏新武杨成全徐永丽
苏新武,林 海,杨成全,徐永丽
(山西大同大学物理与电子科学学院,山西大同 037009)
THz波是指频率在0.1-10THz(波长30μm-3mm)之间的电磁波,其波段位于微波和红外光之间.由于THz波所处的特殊电磁波谱位置,它有非常重要的学术和应用价值.近年来由于超快激光技术的迅速发展,使THz辐射技术和应用研究得到蓬勃发展[1].日本于1997年首次实现了基于非线性LiNbO3光学参量振荡器结构的THz电磁波参量振荡器[2].本文从固体的元激发理论出发,运用声子的受激散射原理阐述了THz波参量振荡器产生THz电磁波的机理,为进一步优化THz电磁波参量振荡器提供了理论依据.
1 TH z波产生的机理分析
固体物质系统处于基态时,晶格原子静止在平衡位置,是一种有序的状态.能量靠近基态的低激发态往往可以看成是一些独立的基本激发单元的集合,这些基本激发单元称为元激发[3],对此可用不同的能量载子把它量子化.晶体在光的作用下,使系统处于激发态,原子偏离平衡位置做微小振动.对于晶体,由于存在周期性振动,原子小振动的集体运动用格波来表示.由于每个格波的能量取值是可以量子化的,这些能量载子就是声子,它是固体中典型的元激发.声子包括声学声子和光学声子,相应的格波分别为声学波和光学波,而光学波对于离子晶体的情形是极化波,极化波则引起固体内部的电极化,使入射光发生散射;这种散射称为喇曼散射.

图1 电磁耦合场量子的色散曲线
当抽运激光束入射到极性LiNbO3晶体时将会激发产生光学波.对于晶体中激发的光学波既可以由喇曼过程来激发,又可以由红外吸收过程来激发.因为横振动的长光学波Q(长光学横波)伴有电磁场.于是,当强度足够大的抽运激光射入晶体时,光波就会和晶体中的长光学横波相互作用、相互耦合,产生的混合激发波就是所谓的电磁耦合场量子,或称为极化声子[4~6](Polariton),它服从声子色散曲线.图1为电磁耦合场量子的色散曲线.电磁耦合场量子具有两重性,既具有晶格振动的特征又有电磁振动的性质.从图中可知耦合场振荡在波长很小范围内,耦合场振荡主要保持着晶格振动的特征,此时电磁耦合场量子主要是TO声子的性质,耦合场振荡在波长很长范围内,主要保持着电磁振动的性质,电磁耦合场量子主要是光子的性质,也就是说在能量较大的范围内主要是喇曼散射过程.相反能量较小范围内主要是参量发生作用的过程.在这一过程中便会产生在THz频率范围的电磁波也就是THz波和斯托克斯光.在这里我们把斯托克斯波定义为闲频波(idler),THz波叫做信号波.在斯托克斯波和THz波通过参量产生的过程中,它们的频率由能量守恒ωP=ωT+ωi和相位匹配条件kP=kT+i所确定,如图2所示.

图2 相位匹配条件
2 TH z波增益计算
受激极化声子散射这一过程可看作是参量产生过程和受激喇曼过程的组合[7~10],在这些过程中它涉及四个相互作用的波:抽用光EP,闲频光Ei,信号光ET和横光学格波.假设这些光波都为平面波,则光电场都能分解为无限大平面波的集合,则有:
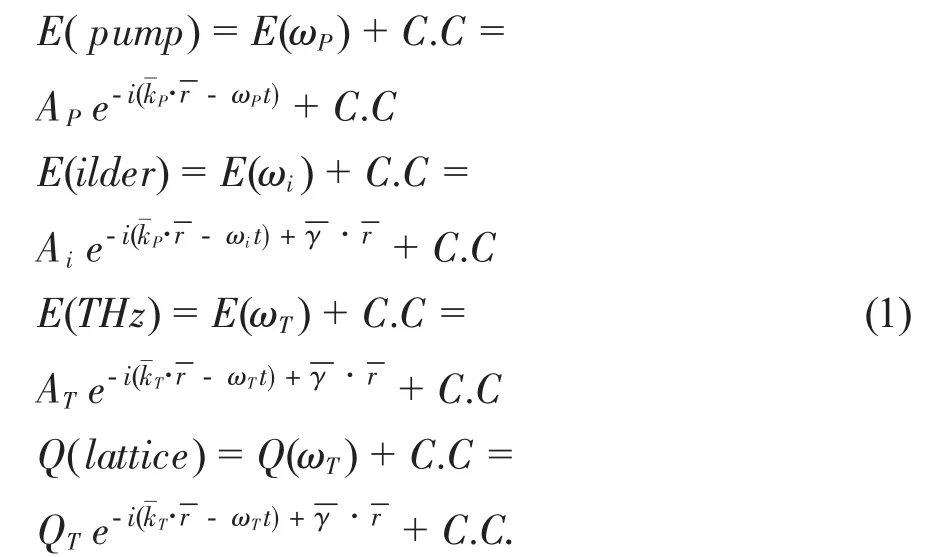
在稳态情况下它分别服从波动方程和格波力学方程:
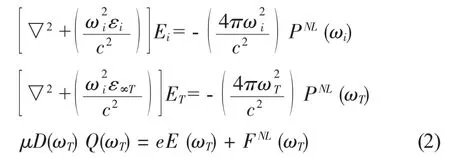
假定在波与波相互作用的过程中存在一个有效相互作用能:
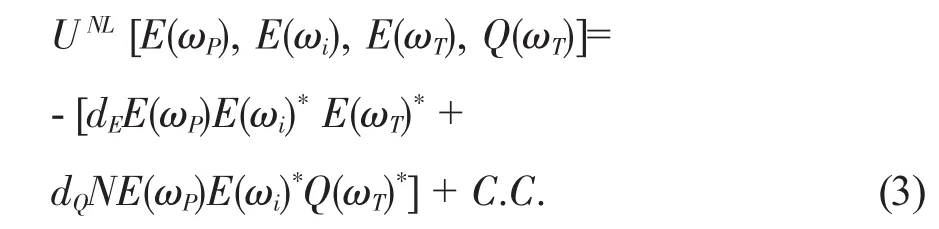
(3)式中N是介质晶体中原胞的密度,dE表示二阶参量过程的非线性系数,dQ表示三阶喇曼散射过程的非线性系数.非线性极化强度PNL和非线性力FNL由下式给出


闲频光和THz光的增益分别定义为
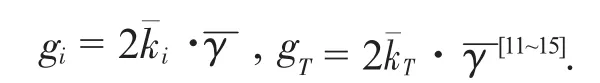
方程有解的条件是特征方程为零,把此特征方程展开,忽略γ的二次项有:
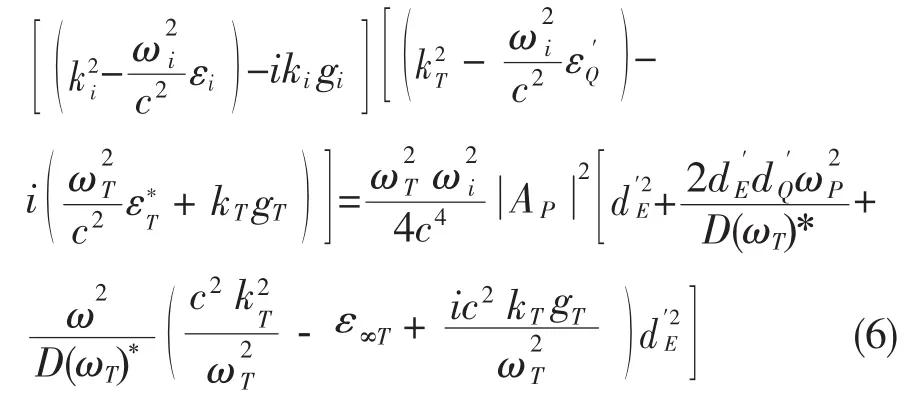
闲频波的复线性波矢可表示为:
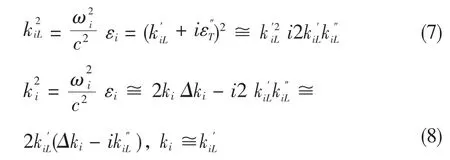
其中,Δki=ki-kiL为相位匹配量.同理可得:
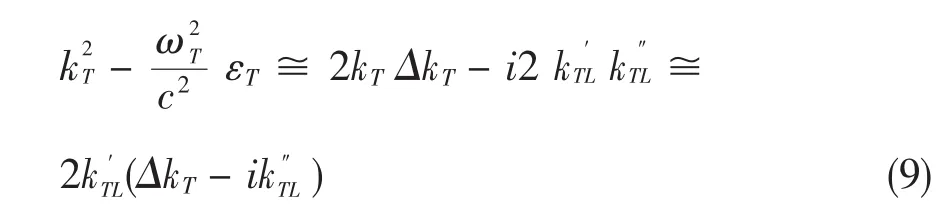
将式(7)(8)(9)带入(6)式得:
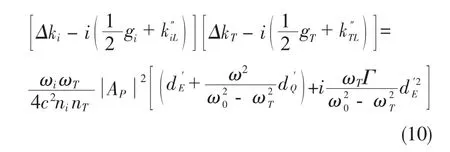
在相位匹配时有Δk=0,LiNbO3晶体对于斯托克斯光来说几乎是透明的则有THz波在LiNbO3晶体中的吸收系数较大,定义因为闲频光和抽运光的夹角很小且它们间的关系为gT=g cos φ ≅ cos φ,则式(10)可表示为:

由于方程(11)左边为实数,则方程右边的虚部应为零,方程右边的实数部分定义为在没有损失的情况下的参量增益g0,则有
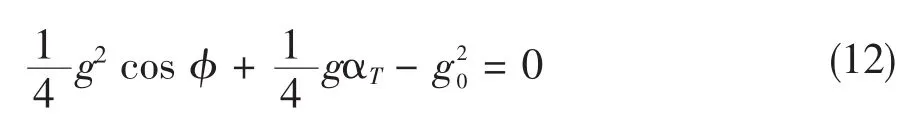
其中,

解方程(12)得

则THz波的增益应为
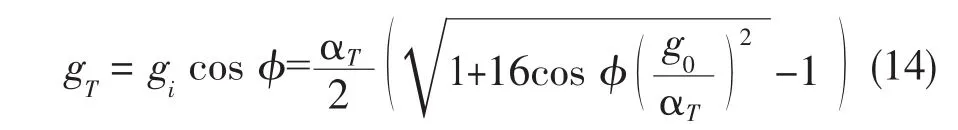
3 结论
运用Henry和Garrett的波耦合方法并考虑了LiNbO3晶体对THz波的吸收损失,给出了THz波参量增益式的详细推导过程,得出了THz波参量增益计算式.为进一步研究THz电磁波参量振荡器提供了理论依据.
[1]王少宏,许景周,汪力,等.THz技术的应用及展望[M].物理,2001,30:612-615.
[2]Yuuki Watanabe,Kodo Kawase,Tomofumi Ikari.Spatial pattern separation of chemicals and frequency independent components by terahertz spectroscopic imaging[J].Applied Optics,2003,42(85):5744-5748.
[3]方俊鑫,陆栋.固体物理学(下册)[M].上海:科学技术出版社,1981:190-202.
[4]M·卡多纳.固体中的光散射[M].北京:科学出版社,1986:326-331.
[5]石顺祥,陈国夫,赵卫,等.非线性光学[M].西安:西安电子科技大学出版社,2003:273-274.
[6]Shen Y R.Nonlinear Infrared Generation[M].New York:Springer Verlag Berlin Heidelberg,1977.
[7]Sussman S S.Tunable light scattering from transverse optical modes in lithium niobate.Stanford[J].CA:Microwave Lab,Stanford University,1970:1851.
[8]Henry C H,Garrett C G B.Theory of Parametric Gain near a Lattice Resonace[J].Phys Rev,1968,171(3):1058-1064.
[9]Barker A S,Loudon J R R.Response functions in the theory of Raman scattering by vibrational and polariton modes in dielectric crystals[J].Rev Mod Phys,1972,44:18-47.
[10]Schwartz U T,Max Maier.Damping mechanism of phonon polaritons,exploited by stimulated Raman gain measurements[J].Phys Rev B,1998,58:766-775.
[11]Junichi Shikata,Kodo Kawase,Manabu Sato,et al.Characteristics of coherent terahertz wave generation from LiNbO3optical parametric oscillator[J].Electronics and Communications,1998,J81-C-1(5):267-273.
