运用Kalman滤波技术校正地下水流系统确定—随机性数值模型
2010-03-19孙永泉刘梅侠董学良陈兴国
孙永泉,刘梅侠,董学良,陈兴国
(1.黑龙江省904水文地质工程地质勘察院,双城 150100;2.大庆市环宇地质工程有限公司,黑龙江 大庆 163000)
1 Kalman滤波技术的基本原理
1.1 Kalman滤波技术的概念
Kalman滤波技术[1]是指用观测数据,采用线形系统状态方程和测量方程作出某一时刻的测量值的最优估计,并希望估计具有递推解。
1.2 Kalman滤波技术的基本原理
卡尔曼滤波有两个基本方程[2]:即状态方程和测量方程。对地下水流系统而言。状态方程是描述地下水流系统确定—随机性问题的方程式,若定义地下水流系统变量为水头矢量H,则地下水流系统的状态方程式为:
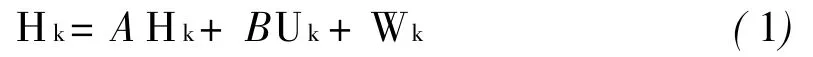
地下水流系统的测量方程为:

式中Yk为k时刻地下水系统状态的测量矢量;Vk为k时刻地下水系统状态的测量误差矢量;为k时刻地下水系统状态的测量矩阵,由监测孔相对于模型分节点的位置确定。
式(1)和式(2)构成地下水流系统确定—随机性数值模型。该模型的求解可按卡尔曼滤波算法求得,其基本假设条件为[3]:
1)系统噪声向量的数学期望为已知函数,即:

2)测量误差向量的期望值为零,即

3)测量误差的协方差阵Rk为

4)系统噪声的协方差阵Qk为
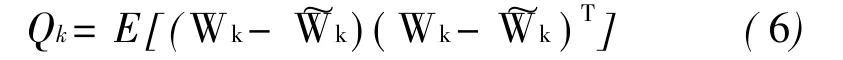
5)系统噪声与测量误差向量相互独立,即:

在上式假设条件下,经过一系列数学推导,得到卡尔曼滤波最优估计的递推算法,即:

及地下水流系统模拟递推算法为:
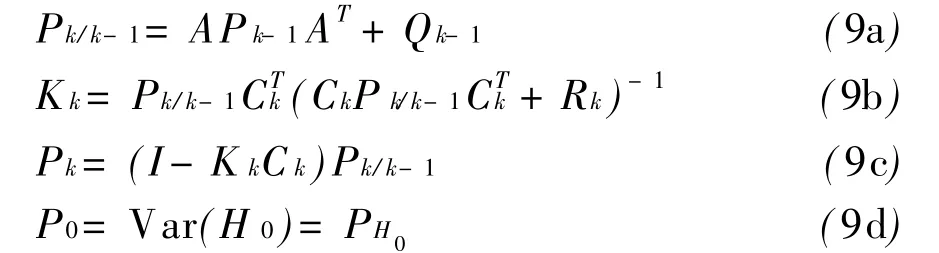
1.3 Kalman滤波技术应用于地下水流系统确定—随机性模型校正
运用卡尔曼滤波最优估计算法,对已建立的模型进行校正,以确定系统参数A、B及Q。对于有限元法的不规则三角剖分而言[4]:

式中G与D分别为有限元方程中的导水矩阵及贮水矩阵;B1为输入项有关的矩阵。通过求解A、B可确定地下水流系统的确定性参数K(或T),S(或μ)等。


式中ρ l为两个节点间(i,j)单位距离上的系统噪声相关系数;dij为i,j两点之间的距离,当i=j时,dij=0。
在进行模型校正过程中,一般按正演方法求解[5],事先给定K,S,ρ1,σ2的初值,运用卡尔曼滤波最优估计算法计算,可得到新息矢量Nk、新息的理论方差矢量Z2、样本方差矢量S2及样本均值矢量¯N,可根据以下统计分析方法,在给定参数估计的可靠度后,按概率统计方法判别模型校正是否满意[6-7]。
由于新息矢量可表达为:

从理论上讲,新息矢量的数学期望应满足:

新息矢量的理论方差为:
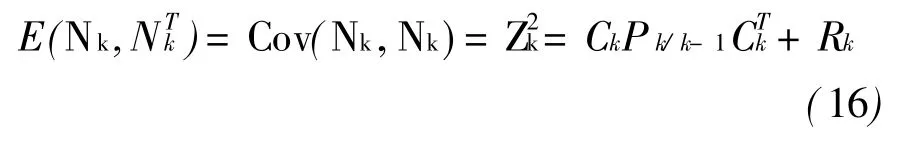
新息矢量的样本均值为:

新息矢量的样本方差为:

理论上讲,若给定含水层系统确定性参数(K,S等),随机性参数能使新息的均值和方差满足下式:

则所确定的参数是最佳模型参数,参数的可靠性为100%,此时模型校正结束。实际中由于样本数NT有限及计算误差及系统误差的存在,实际上求得¯N≠0,S2≠Z2。为了给 ¯N,S2赋予一个明确的精度概念,引入均值和方差的置信区间,只要 ¯N,S2在一定的置信区间内,则认为模型校正结束,所确定的参数满足一定的精度。
1.3.1 用S2确定总体均值的置信区间
新息矢量Nk为总体N(0,Z2)的一簇样本,用样本方差S2估计Z2,则[8-9]:

且t(NT-1)分布不依赖于总体均值,从而得:
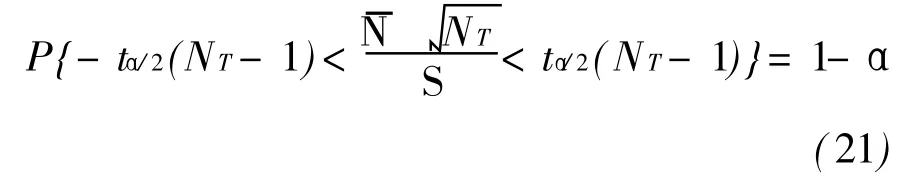
于是,得均值为零(Nk=0)的置信度为1-α的置信区间为:
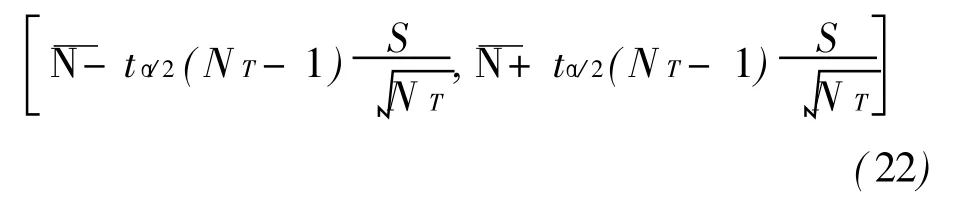
1.3.2 方差Z2的置信区间
由于
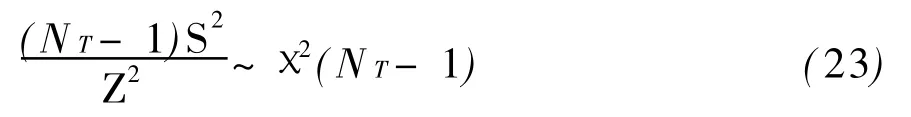
且χ2(NT-1)分布与Z2无关,则有:
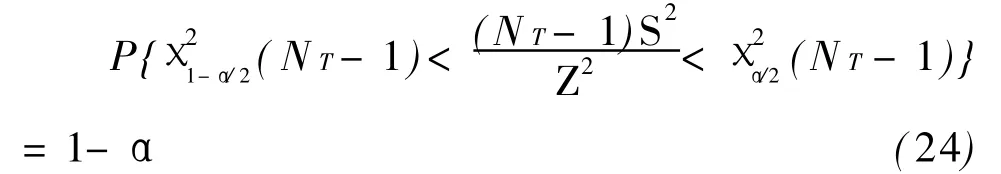
于是,得方差Z2置信度为1-α置信区间为:
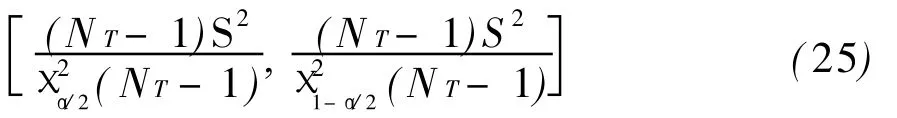
如果全部均值和方差都通过检验,则可得出结论,卡尔曼滤波与地下水流数值耦合模型已得到很好地校正[10],其可信度为1-α。
2 实 例
2.1 地下水流系统数学模型
研究区面积约8 000 km2,主要取水层位为第三系承压含水层。历经30 a的开采,已形成了4 000 km2的地下水位降落漏斗,并积累了大量的动态资料。研究区东部为第三系承压水缺失边界,南部、西部和北部为已知水头边界。研究区地下水径流方向为北北西向,主要补给方式为侧向径流补给,其次为垂向补给,主要排泄方式为人工开采,依据上述含水层系统特征,研究区渗流问题的数学模型可描述为[11]:
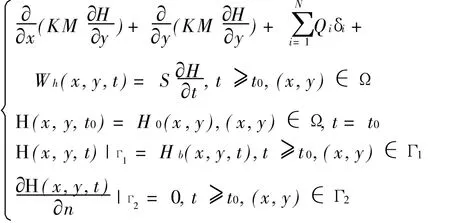
式中Wh(x,y,t)为地下水流模型中的随机误差项,也称系统噪声,它包括实际地下水系统概化成模型引起的误差、边界条件概化、初始条件概化引起的误差等项;H(x,y,t)为渗流域中任意时刻的地下水头分布值(或称地下水流系统的状态)(m);K M为含水层的导水系数(m2/d),K为含水层的渗透系数(m/d),M为含水层的厚度(m);S为含水层的贮水系数,无量纲;H0(x,y)为渗流域中初始水头分布或称地下水流系统的初始状态(m);Hb(x,y,t)为渗流域中已知边界水头分布(m);Qi为渗流域中i节点上源汇项;Ω为渗流域;Γ1为渗流域中已知水头(第一类)边界;Γ2为渗流域中已知流量(第二类)边界。
研究区离散为688个三角形单元,383个节点,初步划分为18个确定性参数区和13个随机性参数区。
2.2 模型校正
运用前述的卡尔曼滤波最优估计递推算法,选取已知监测孔20个(选取原则:①保证每个参数区至少有1个监测孔;②实测值中缺失较多者不选),计算时段选在1986年1月至1993年12月,在此时间段内监测孔数量较多,监测序列连续性好。测量误差的方差取为0.002 5 m2。校正后的渗透系数、贮水系数和系统噪声标准差见表1,表2,系数ρl的校正值为0.85。

表1 校正后的模型确定性参数表T able 1 Certaintyof the model parameter table afer correcting
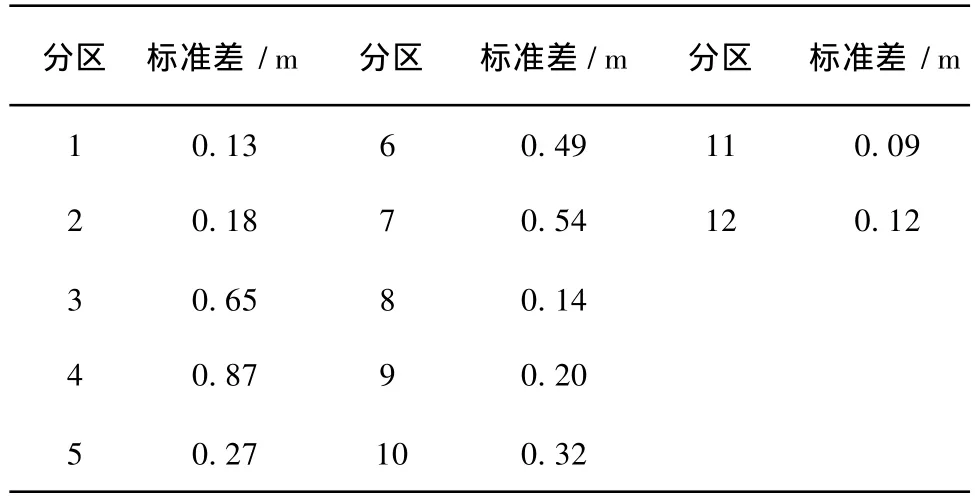
表2 校正后的模型的随机性参数表T able 2 Randomness of the model parameter table afer correcting
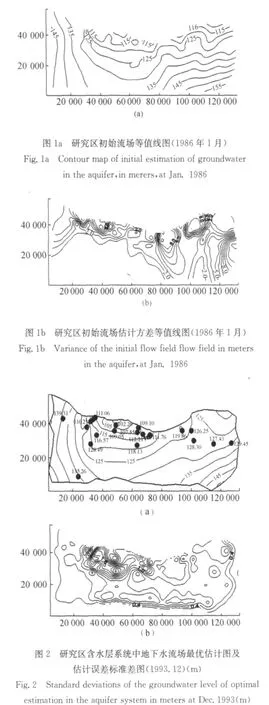
图1、图2分别为研究区初始流场等值线图和估计方差等值线图及最优估计流场和标准差等值线图,从图2a和图2b(为最优估计误差标准差图)可以看出,计算的地下水流场和实际的地下水流场拟合的比较好,因此,计算的地下水流场基本上代表了地下水位的空间分布特征,说明模型正确地描述了含水层系统的基本特征。同时对20个监测孔的历时曲线进行了对比,除7119、7101、7208 3个孔拟合较差外,其余17个孔拟合程度很好。每个监测孔新息的均值见表3,表4和表5为模型校正可靠性的检验结果。
由表3可见:7119、7101、7208、8208、8409 5个孔的新息值较大。由表 4的 t检验可见:7119、7101、7208、8208及8409 5个孔未通过检验,可能是由于观测精度及观测序列中有缺失数据引起的,其余15个孔新息的均值与零无明显差异。由表5可见,除7114、7207、8208 3个孔未通过χ2检验外,其余17个孔全部通过χ2检验,这几个孔未通过χ2检验的主要原因是系统噪声标准差高及新息样本标准差太大。要想全部通过t和χ2检验是十分困难的,只要大多数孔通过检验就可以了。通过模型校正,可认为校正后的模型基本上反映了实际的水文地质特征及地下水流系统特征,可靠性达90%以上(模型正检验时选取置信度95%)。

表3 已知监测孔新息的均值表Table 3 Known monitoring holes mean of the new interest rate table /m
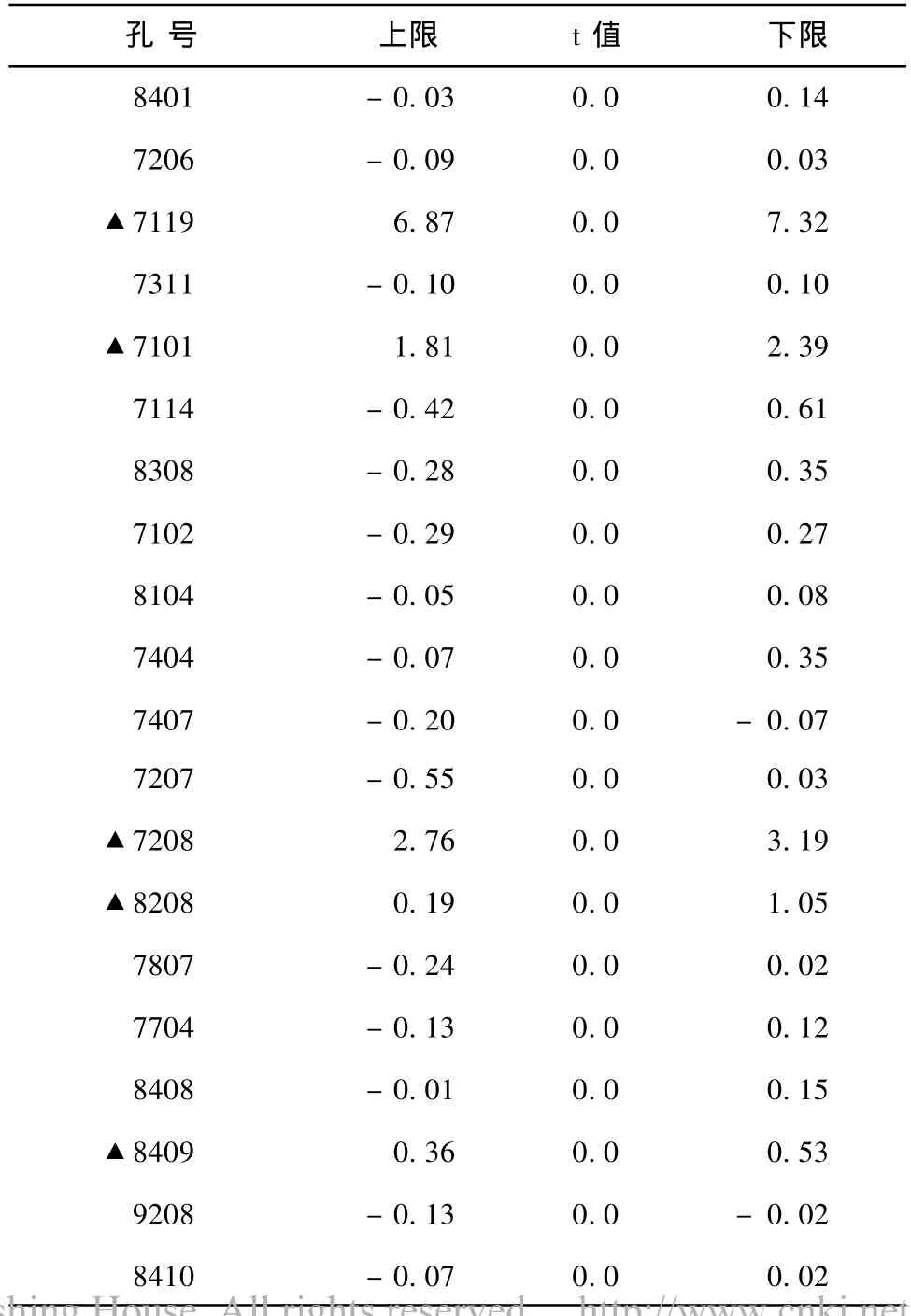
表4 已知监测孔的新息均值的t检验T able 4 Known monitoring holes of the newrate means-t test

表5 已知监测孔的新息标准差的检验Table 5 Known monitoring holes test of the new interest rate standard deviation
3 结 论
本文运用了卡尔曼滤波技术校正地下水流系统,提出一种估计地下水流系统的随机性参数的卡尔曼滤波耦合算法。通过对研究区地下水流系统的分析,可以得出以下结论:
1)本文的方法既考虑了地下水系统的确定性,又考虑了随机性。
2)本文的方法可估计地下水流系统分布式参数,包括确定性参数和随机性参数,并可给出参数估计的置信区间和精度。
3)估计的研究区地下水流系统分布型参数的可靠性达90%以上。
[1] 李官锡,贾洪利,周福俊,等.大庆西部地区地下水补给条件及水质的研究[R].大庆:大庆石油管理局供水公司,1991.
[2] 李俊亭.地下水流数值模拟[M].北京:地质出版社,1989.
[3] J.Bear.地下水水力学[M].北京:地质出版社,1985.
[4] 仵彦卿.地下水系统的基本概念与组成[J].长安大学学报(地球科学版),1990,12(4):88-91.
[5] 戴冠中,佟明安.现代控制理论导论[M].北京:国防工业出版社,1989.
[6] 高钟毓.工程系统中的随机过程——随机系统分析与最优滤波[M].北京:清华大学出版社,1989.
[7] 浙江大学数学系高等数学教研组.概率论与数理统计[M].北京:高等教育出版社,1979.
[8] F.C.Van Geer,Van der Kloet P.Estimation of Parameters in Groundwater Flow Problems Using a Kalman Filter Algorithm [J].Symposium International,TNO Comm.Hydrol.Res.T he Hague,1983:449-462.
[9] F.C.Van Geer,C.B.M.Te Stroet,Zhou Yangxiao.Using Kalman Filtering to Improve and Quantify the U ncertainty of Numerical Groundwater Simulations 1:T he Role of System Noise and Its Calibration[J].Water Resour.Res.,1991,27 (8):1 987-1 994.
[10] F.C.Van Geer.Applicatiop of Kalman Filtering in the Analysis and Design of Groundwater Monitoring Networks[R].Report,Delft Univ.of T echnol.,Delft,Netherlands,1987.
[11] Zhou Yangx iao,C.B.M.T e Stroet,F.C.Van Geer.Using Kalman Filtering to Improve and Quantity the Uncertainty of Numerical Groundwater Simulation 2:Application to M onitoring Network Design[J].Water Resource.Res.,1991,27(8): 1 995-2 006.
