基于RAGA的PPC模型在黑龙江省洪水灾害综合评价应用研究

吕福财，付 强，朱建华，周 兵

(1.东北农业大学，哈尔滨150030;2.穆棱市水利勘测设计队，黑龙江穆棱157500)

1 引言

洪水灾害损失评价就是根据已有灾情指标值建立灾情评价模型，对因洪水灾害造成的破坏程度进行评价。黑龙江省是我国主要的粮食产地，全省境内江河湖泊众多，有黑龙江、乌苏里江、松花江、嫩江和绥芬河五大水系，现有湖泊、水库6 000余个，水面达80多万公顷。及时有效地对黑龙江省进行洪水灾害损失评价工作，对洪水灾害管理工作和灾害的救济具有重要的指导意义。

洪水灾情涉及自然环境与社会经济等许多因素，目前国内外尚无统一的洪水灾情评估指标体系和对各指标的灾情等级标准，洪水灾害损失灾情评价至今仍是洪灾研究的难点和热点之一。我国在洪水灾害损失评价方面相继提出了灾度判别法、模糊综合评判、物元分析、神经网络等灾情等级模型［1－4］，但上述方法需要灾情评价的标准。黑龙江省正是没用洪水灾害损失的评价标准或标准已经不适用，因而一直无法对其进行洪灾损失的评价分析。本文将改进的GA方法—基于实数编码的加速遗传算法(Real coding based Accelerating Genetic Algorithm，简称 RAGA)与投影寻踪分类模型(Projection Pursuit Classification Model，简称PPC模型)有机结合［5］，通过RAGA优化PPC模型中的投影方向参数，完成高维数据向低维空间的转换，即将每个样本的多个评价指标综合成一个综合指标，然后按投影值进行排序与识别，从而实现对黑龙江省洪水灾害损失评价。为没有评价指标标准的评价研究提供一条新的方法与思路。

2 PPC模型［6－8］

投影寻踪分类模型(Projection Pursuit Classification Model，简称PPC)的建模过程包括如下几步:

步骤1:样本评价指标集的归一化处理。设各指标值的样本集为{x*(i，j)|i=1，2，…，n，j=1，2，…，p}，其中x*(i，j)为第i个样本第j个指标值，n、p分别为样本的个数(样本容量)和指标的数目。为消除各指标值的量纲和统一各指标值的变化范围，可采用下式进行极值归一化处理例如对于越小越优的指标:

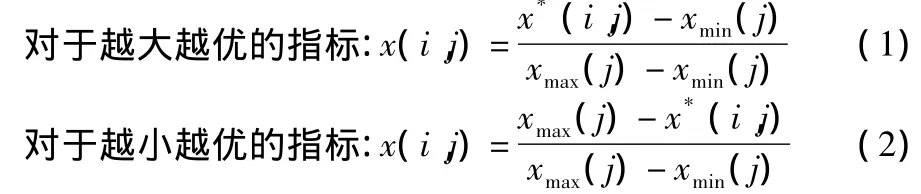
其中，xmax(j)、xmin(j)分别为第j个指标值的最大值和最小值，x(i，j)为指标特征值归一化的序列。

步骤2:构造投影指标函数Q(a)。PP方法就是把p维数据{x(i，j)|j=1，2，…，p}综合成以a={a(1)，a(2)，a(3)，…，a(p)}为投影方向的一维投影值z(i):

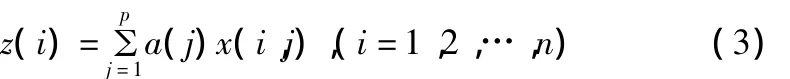
然后根据{z(i)|i=1，2，…，n}的一维散布图进行分类。式(3)中a为单位长度向量。综合投影指标值时，要求投影值z(i)的散布特征应为:局部投影点尽可能密集，最好凝聚成若干个点团;而在整体上投影点团之间尽可能散开。因此。投影指标函数可以表达成:

其中，Sz为投影值z(i)的标准差，Dz为投影值z(i)的局部密度，即:

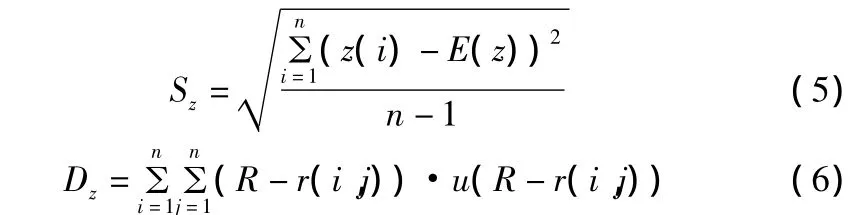
其中，E(z)为序列{z(i)|i=1，2，…，n}的平均值;R为局部密度的窗口半径，它的选取既要使包含在窗口内的投影点的平均个数不太少，避免滑动平均偏差太大，又不能使它随着n的增大而增加太高，R可以根据试验来确定;r(i，j)表示样本之间的距离，r(i，j)=|z(i)－z(j)|;u(t)为一单位阶跃函数，当t≥0时，其值为1，当t<0时其函数值为0。

步骤3:优化投影指标函数。当各指标值的样本集给定时，投影指标函数Q(a)只随着投影方向a的变化而变化。不同的投影方向反映不同的数据结构特征，最佳投影方向就是最大可能暴露高维数据某类特征结构的投影方向，因此可以通过求解投影指标函数最大化问题来估计最佳投影方向，即:

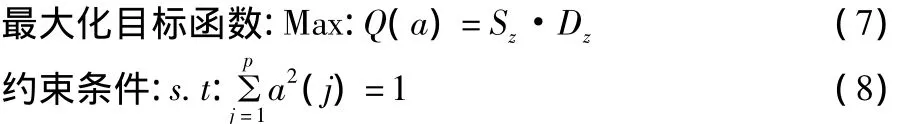
这是一个以{a(j)|j=1，2，…，p}为优化变量的复杂非线性优化问题，用传统的优化方法处理较难。因此，本文应用模拟生物优胜劣汰与群体内部染色体信息交换机制的基于实数编码的加速遗传算法(Real coded Accelerating Genetic Algorithm，简称RAGA)来解决其高维全局寻优问题(RAGA的结构在下节介绍)。

步骤4:分类(优序排列)。把由步骤3求得的最佳投影方向a*代入式(3)后可得各样本点的投影值Z*(i)。将z*i与z*(j)进行比较，二者越接近，表示样本i与j越倾向于分为同一类。若按z*(i)值从大到小排序，则可以将样本从优到劣进行排序。

3 基于实数编码的加速遗传算法［9－10］

遗传算法由美国密执安大学的Holland教授提出的，是模拟生物在自然环境中的遗传和进化过程而形成的一种自适应全局优化概率搜索算法。主要包括选择(selection)、交叉(crossover)和变异(mutation)等操作。例如求解如下最优化问题:Maxf(x)，st，a(j)≤x(j)≤b(j)。

共有8个步骤:①在各个决策变量的取值变化区间随机生成N组均匀分布的随机变量;②计算目标函数值，从大到小排列;③计算基于序的评价函数(用eval(V)表示);④进行选择操作，产生新的种群;⑤对步骤④产生的新种群进行交叉操作;⑥对步骤⑤产生的新种群进行变异操作;⑦进化迭代;⑧上述⑦个步骤构成标准遗传算法(SGA)。由于SGA不能保证全局收敛性，在实际应用中常出现在远离全局最优点的地方SGA即停滞寻优工作。为此，可以采用第1次、第2次进化迭代所产生的优秀个体的变量变化区间作为变量新的初始变化区间，算法进入步骤①，重新运行SGA，形成加速运行，则优秀个体区间将逐渐缩小，与最优点的距离越来越近。直到最优个体的优化准则函数值小于某一设定值或算法运行达到预定加速次数，结束整个算法运行。此时，将当前群体中最佳个体指定为RAGA的结果。上述8个步骤构成基于实码的加速遗传算法(RAGA)。

4 应用实例

灾情资料取自《黑龙江省防汛资料汇编》。

表1中为黑龙江省1992－2001年的洪水灾害损失的10个评价样本，每个样本有7个评价指标，即属于7维数据。对表1中黑龙江省洪水灾害损失的10个评价样本建立综合效益分类评价的PPC模型。RAGA过程中选定父代初始种群规模为N=400，交叉概率PC=0.80，变异概率pm=0.8c，优秀个体数目选定为20个，a=0.05，加速次数为20，得出密度窗宽R=7.9170，最大投影值943.0534，最佳投影方向a*= (0.3993，0.4040，0.3988，0.0352，0.4071，0.4199，0.4185)，将a*带入式(3)中即得黑龙江省洪水灾害损失的投影值(见图1)为:z*(i)=(0.1473，0.1394，0.7833，0.0937，0.2309，0.2855，2.4494，0.1366，0.0434，0.0323)。

表1 黑龙江省洪水灾害灾情评价指标原始数据

从图1可以看出，黑龙江省1992－2001年10 a间有两年的洪灾损失非常严重，分别为1998和1994两年的投影值分别为2.4494和0.7833比其他年份均高可以肯定这两年的损失严重。1994年的评价结果与潘华盛［11］利用模糊综合评价法的结论相符;1998年松花江、嫩江发生了超百年一遇的特大洪水，黑龙江省洪水损失达到历史洪水灾害损失最大。由此，说明了再不需要评价标准的情况下，RAGA的PPC模型的评价结果可靠。

另外，最佳投影方向各分量的大小实际上反映了各评价指标对洪水灾害损失的影响程度(见图2)，最佳投影方向a*表明，各评价指标对洪水灾害损失评价的影响程度大小依次为直接经济损失、水利设施经济损失、房屋倒塌数、洪涝的成灾面积、洪涝的受灾面积、受灾人口、死亡人口。由此可以看出洪水灾害损失实质主要是经济的损失，为防洪减灾的有关部门提供了及时有效地减灾救灾依据。

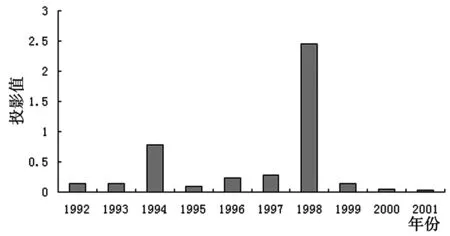
图1 1992～2001年黑龙江省洪水灾害损失的投影值z*(i)

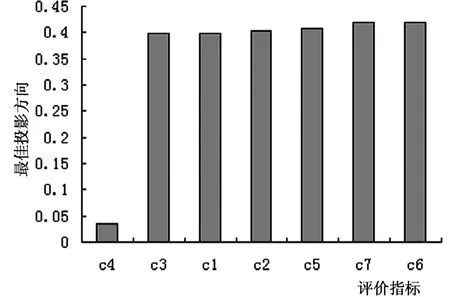
图2 黑龙江省洪水灾害损失综合评价指标的投影方向a*

5 结语

黑龙江省在洪水灾害无评价标准或评价标准不适用的情况下，尝试了不用评价标准的RAGA的PPC模型进行了1992－2001年10 a的洪水灾害损失评价工作。实例的计算结果说明，该方法避免了主观赋权的人为干扰，取得了较好效果，为没有评价指标标准的评价研究提供一条新的方法与思路;并且分析了各指标的影响程度，为防洪减灾提供了依据。

［1］ 金菊良，魏一鸣，杨晓华.基于遗传算法的洪水灾情评估神经网络模型探讨［J］.灾害学，1998，13(2):6－11.

［2］ 于庆东.灾度等级判别方法的局限性及其改进［J］.自然灾害学报，1993，2(2):8－10.

［3］ 赵黎明，王康，邱佩华.灾害综合评估研究［J］.系统工程理论与实践，1997，17(3):63－69.

［4］ 李祚泳，邓新民.自然灾害的物元分析灾情评估模型初探［J］.自然灾害学报，1994，3(2):28－33.

［5］ 付强，赵小勇.投影寻踪模型原理及其应用［M］.北京:科学出版社，2006.

［6］ 付强，王志良，梁川.基于RAGA的PPC模型在土壤质量变化评价中的应用研究［J］.水土保持学报，2002，16(5):109－110.

［7］ 项静恬，史久恩.非线性系统中数据处理的统计方法［M］.北京:科学出版社，2000.

［8］ 张欣莉.投影寻踪及其在水文水资源中的应用［M］.成都:四川大学，2000.

［9］ 周明，孙树栋.遗传算法原理及其应用［M］.北京:国防工业出版社，2000.

［10］ 付强.数据处理方法及其农业应用［M］.北京:科学出版社，2006.

［11］ 潘华盛，张桂华，董淑华.黑龙江省洪水灾害等级评估模型—模糊综合评价法［J］.黑龙江气象，2000，2(1):1－4.