智能代理模拟在电力市场中的运用*

王野平 杨彦† 荆朝霞 陈皓勇 陈天恩

(1.华南理工大学电力学院,广东广州 510640;2.西北电网有限公司,陕西西安 710048)

当前我国电力市场化改革已经迈出了实质性步伐,取得了一系列重要成果,但是电力市场机制设计与运行是个相当复杂的课题,建设完善健全的电力市场是个困难的过程,对经济界和电力工业界提出了理论与实践的双重挑战.

英国、北欧等电力市场的成功运行为我国电力市场的建设提供了众多可借鉴的经验,但也有一些电力市场经历了失败.美国加州电力市场曾出现电价居高不下,导致部分电力公司巨额亏损濒临破产;国内试运行的东北电力市场出现平衡账户亏空严重,导致市场被迫停滞.可见目前条件下,建立电力市场对电力系统的运行存在风险.因此,为了把风险化解在方案设计和规则制定阶段,在电力市场正式启动之前,有必要密切结合电网实际,建立相应的电力市场模拟系统,用于研究分析各种市场方案和规则的合理性.这既可以为市场参与实体的交易员进行培训提供有效的技术支持,也可以进行市场的模拟仿真,以便分析市场缺陷.

构建电力市场模拟系统成为现今电力市场领域的研究热点,面临众多亟需解决的问题[1],其中如何模拟发电厂商的竞价行为是最重要的课题之一.人工智能领域的智能代理技术于上世纪 70年代面世以来备受关注,特别适合处理具有复杂关联且难以运用传统数学理论精确分析的问题.基于智能代理的模拟仿真已经成为一种有效的实验工具[2],在复杂社会系统的研究中有广泛运用,同时也成为研究各种电力市场机制的重要途径.

国际上较有代表性的相关研究有:Bower等[3]为研究英国电力市场交易规则建立了简单的市场仿真器,以发电厂商利润与机组利用率为综合目标,构造了根据上两轮市场信息做简单推理决策的代理模块;美国衣阿华州州立大学Tesfatsion教授等[4]为研究联邦能源管理委员会提出的批发电力市场规则,开发了电力市场代理仿真系统(AMES),运用VRE learning算法作为决策核心;美国康奈尔大学Zimmerman等[5]构建了基于网络的实验平台Power Web系统,用随机报价等方法构建代理决策规则;美国Agone国家实验室开发了复杂电力市场自适应系统(EMCAS)[6],主要利用电价预测与贪婪算法为代理提供决策功能.

国内关于电力市场模拟系统的研究亦在开展之中:文献[7]中介绍了电力市场仿真和培训系统的设计及实现,对电力市场仿真系统的建设具有重要的理论参考价值,但其还未具有发电厂商报价决策功能;文献[8]中探讨了电力市场与电力系统动态的交互仿真平台的建设;文献[9]中采用人工网络技术和博弈论方法建立了电力竞价上网智能决策支持系统;文献[10]中为分析在节点电价运行方式下的市场特征,运用了VRE learning算法构建了发电厂商的决策模型;文献[11]中构造了电力市场模拟仿真的多代理模型,并用猜测供给函数算法为代理提供决策支持;文献[12]中指出Q-learning算法能够较好地模拟发电厂商的经济特性.

文中主要工作是结合某一实际区域(文中称为W区域)电力市场模拟系统的构建,研究实现了适合模拟发电厂商决策报价的智能代理学习算法,其中包括属于强化学习的Q-learning、VRE learning算法以及贪婪算法.多种智能代理学习算法的实现为仿真研究发电厂商的市场行为与分析市场性质提供了多样选择,是实现电力市场仿真模拟系统智能化的关键.

1 强化学习

强化学习通过感知环境并从环境中获得不确定信息以寻找动态系统的最优策略.在许多复杂领域,强化学习是对代理进行决策目标训练以获得有效性能的可行途径[13],VRE learning算法及Q-learning算法是强化学习中两种重要的方法,均被运用来构建电力市场模拟系统中的报价决策模块.

强化学习算法的基础是构建能够恰当简便地描述发电厂商竞价行为的策略集,这里根据 W区域电力市场的运行规则,首先介绍模拟系统中发电厂商代理的策略集,然后分析探讨了两种算法的运用.

1.1 代理(发电厂商)的策略集

当前电力市场具有寡头垄断市场性质,发电厂商能够以高于边际成本的竞价获得高额利润.策略集根据发电厂商的发电成本来构建,以发电厂商 i为例,根据市场规则及系统设计方案,其成本函数ci(qGi)可以用分段函数表达:

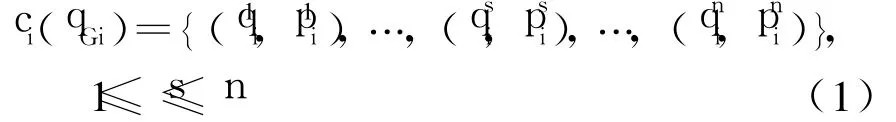
式中:qGi为代理i拥有的所有发电容量分别为第s竞价段的容量与电价;n为函数的总段数.假定成本函数需要满足以下条件:

代理的策略仅针对成本函数做仿射处理,并且仅将各段函数中的报价做决策变量,即假定代理采用策略系数Ai构建报价函数:

式(2)表示代理的报价不改变成本函数各段的电量,只改变各段的电价.市场规则制定了报价上限,故策略系数需满足:

式中:Ai,min、Ai,max分别为策略系数的上、下限;¯p为市场规定的报价上限.一般而言发电厂商的报价不会低于自己的成本,所以可将Ai,min设置为1.0.将满足式(3)的策略系数平均离散化M份来构建i的策略集,其中的含义如下:

其相应的竞价函数为

1.2 VRE learning算法及应用

VRE learning算法由Roth和Erev[14]在1995年提出,其主要准则来源于生物学习中 3个基本经验: (a)遵守生物学中的条件反射原理,即往前成功的经验在往后的选择中容易被采用;(b)现近的经验比前远的经验更容易被采用;(c)学习速度通常在初始阶段比较快速,随后逐渐变缓.

VRE learning算法的运用框架设计如下:对代理i的每个策略都标志倾向系数φik和概率系数χik作为代理学习与决策的依据.这两个概率系数根据回报收益进行更新,若i在第t轮的竞价中选择了策略,并在该轮得到回报收益rik(t),那对策略集中策略的倾向系数更新如下:

式中:Rim(t)为响应函数,计算如下.

式(6)中的 ω为遗忘因子,对策略的倾向系数起着随时间增加的抑制作用,引入因子的目的就是减弱往前经验的影响,增强现近的经验作用;式(7)中的e为经验因子,对往前成功的经验起到鼓励作用.

将策略Smi在整个策略集对应轮盘赌中所占的概率定义为概率系数,计算如下:

式(8)采用了模拟退火的思想,运用指数函数来构造概率,使得即使某一策略的收益出现负值导致其对应的倾向系数出现负值,该策略被选择的概率仍为正,这符合选择概率的性质,式中c为冷却系数.

代理根据概率系数,依照轮盘赌的方式选择竞价行为.该算法在决策模块中的运行流程设计如下:

(a)根据i的自身信息设置Ai,min、Ai,max与M,即构建策略集Si;

(c)依据轮盘赌方式进行第t轮决策.假设i在该轮选择了策略向独立调度提交报价

(d)独立调度接受所有代理的报价后,根据所设定的市场出清规则安排发电计划.代理 i根据相应电价与中标电量计算利润πik(t),设定策略Ski获取的回报,即为利润:rik(t)=πik(t);

(e)根据式(6)、(7),更新各策略Smi对应的倾向系数至φim(t+1),即时根据式(8)更新相应的概率系数;

(f)重复步骤(c)～(e),直到满足停止规则.

VRE learning算法在学习过程中根据自身利润不断更新策略决策参数,但未考察外部因素的影响,属于一维学习模式.为了应对外部环境变化,模拟系统还构建了基于Q-learning算法的决策模块.

1.3 Q-learning算法及应用

Q-learning算法是Watkins[15]针对环境的不完全信息而提出的一种强化学习算法.Q-learning算法通过维护一组S(动作)-X(环境)空间上的函数Q值来获得预期整体回报最大化的策略.将环境看作离散状态空间,使用马尔可夫链转移模型和累加回报的这种特定规格的延续式决策问题被称为马尔可夫决策过程(MDP).通常,马尔可夫决策过程可以用一个四元组〈X,S,R,Z〉表示,其中 X为环境状态集;S为代理的策略集;R为回报函数;Z(x,s,x′)是代理在环境状态x X下采用动作s S,使环境迁移到x′所对应的概率.S-X空间的函数值用Q(s,x)来表示,通过学习环境状态之间的联系,函数Q值计算如下:

但运用时序差分方法可不用关心转移模型,而只关注动作 s采取前后的环境状态间的变化情况,因而假设代理在第t轮处于状态 xt,选择动作st得到状态xt+1(即y)与回报rt,得到简化的迭代修正公式:

式中:β为学习因子;η为折扣因子.

运用Q-learning算法构架决策模块的关键是构建合适的S-X空间及回报,这里的处理方式如下.

环境X:选用系统总负荷、市场出清电价及代理中标容量受约束情况 3个因素联合作为区分环境状态的准则,具体区分有:(a)将系统总负荷L[Lmin, Lmax]分为递增的 N份,其中 Lmin、Lmax分别为负荷可能的上、下限;(b)将市场电价加权平均值V[Vmin, Vmax]分为H份,其中Vmin、Vmax分别为市场最低与最高价格;(c)比较代理在有无约束条件下市场出清的中标电量,可分为 3种状态:有约束中标电量等于、大于与小于无约束收购电量.

将上述3种情形综合考虑,将环境分为3NH种状态.

动作S:运用1.1节所构建的策略集作为Q-learning算法的动作集,根据代理的自身信息设置M值、Si,min与Si,max来构建.

回报R:将代理的竞价利润作为回报.

探索方案:Q-learning算法发展至今已有若干重要的探索方案,目前模拟系统运用原始贪婪的探索方案,经过一个预先设定的随机学习阶段后,代理在各种状态下都选取对应Q值最大的动作策略.

Q-learning算法的运行流程与VRE learning算法的步骤基本相同,仅增加了对外部环境的识别及相关功能:在步骤(c)报价时,根据市场发布的信息确定当前的环境状态xt,而后从 xt对应轮盘赌圆盘选择st;在步骤(e)更新学习参数时,先应识别环境状态xt+1后,根据式(11)更新Q值.

从运用框架可见,VRE learning算法属于一维学习模式,认为环境不变,每次报价均试图从轮盘赌中选取概率大的行为;Q-learning算法考虑了不同的环境而扩充为多维学习模式,需先判断系统所处的状态,然后根据状态选择策略行为.

2 贪婪算法及应用

贪婪算法根据代理报价函数各容量段被收购与否的状况来调整其相应容量段的报价,以期达到发电量与利润最大化.该算法的前提条件是报价函数为分段梯形上升曲线,即各容量段的报价递增,W区域电力市场所设定的成本函数及报价函数恰好满足这个要求.

如果报价函数中某容量段全部或部分被收购,而报价更高的容量段未被收购,则将该容量段定义为边际容量段b:(qimb,pimb).为论述方便,将竞价容量段按照报价由低到高标记为1,…,b,…,n.运用贪婪算法构建决策模块,首先需要评估上一轮(记为第t轮)的竞价结果,核定第t轮的边际容量段bt;然后第(t+1)轮的报价是基于第t轮的边际容量段来调整报价的,分以下 3种情况分别处理:

(a)bt=n,即所有的容量段均被收购.那么代理下一轮的报价为

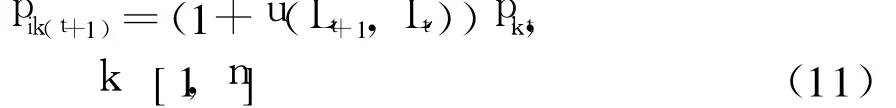
式中:pik(t+1)、pikt分别为代理i在第t+1及t轮时第k容量段的报价;Lt+1、Lt分别为第t+1及t轮的系统总负荷;u(Lt+1,Lt)为代理基于总负荷变化的报价增量函数.式(11)表明代理在第t+1轮的报价是在第 t轮报价基础上根据总负荷的变化上调合适的系数.

(b)bt=0,即所有容量段均未被收购.那么

式(12)表示代理在第t+1轮的各容量段报价是在第t轮的基础上均下调某一百分比uFix.

(c)bt[0,n],即部分容量段被收购.那么:

式(13)表示不高于边际容量段报价的容量段竞价维持上轮的报价,而其它容量段则下降百分比uFix.

贪婪算法体现了发电厂商报价过程中追求更多中标容量与利润的试探心理,算法原理简单,在实验仿真中展现出很好的探索性能,是一种不可或缺的智能代理学习算法.

3 代理学习算法的收敛处理

强化学习算法属于随机决策方法,在一定的学习参数与仿真系统系数设置下,可能使代理的报价策略选择保持不变达到收敛状态.为了便于分析比较实验结果,考察收敛状态下的市场情形具有相当的意义,因此电力市场模拟系统在代理决策收敛问题上对学习算法有如下分析与处理:

(a)VRE learning算法根据策略集对应的轮盘赌概率分布来决定报价,若某策略的选择概率非常接近 1.0,这就意味着代理在往后的竞价中可能总是采取该策略报价,也就是说该代理达到收敛状态.模拟系统若设定某策略的选择概率大于收敛阀值δ,则认为代理达到收敛而停止学习;

(b)贪婪算法根据上一轮报价与出清电价的比较,积极地试探性调整报价.若系统中的其它代理基本上已达稳定状态,市场电价可能会因为基于贪婪算法决策的代理所采取的试探行为而波动,为此,记录该类型代理连续抬高并随后降低报价的波动次数,若波动次数大于系统设定的震荡阀值,则认为代理已经达到收敛状态,往后报价不再改变;

(c)若系统中其它代理基本已达稳定状态,这可能使基于Q-learning算法决策的代理达到收敛:如果系统处于相对稳定的情型,该类型代理面临较为稳定的环境状态,在采用原始贪婪的探索方案下,代理总是选取在该稳定状态下的对应Q值最大的策略,那么代理采取的策略将不变,即该代理也将处于稳定状态.

4 算例及其分析

本节运用W区域电网的实际算例来说明智能代理模型及其学习算法在电力市场模拟系统中的运用情况.根据该区域电力市场运行规则,只允许发电容量大于100MW的火电机组参与市场竞价;其它较小容量火电机组与水电机组不参与市场竞价,仅作为辅助设备参与系统运行.目前该区域电力系统有容量大于100MW的机组102台,其中火电90台,水电厂12家,总装机发电容量为30088MW,其中火电装机容量为21434MW,占总装机容量的71.24%,水电总装机容量为8654MW,占总装机容量的28.76%.

这里以VRE learning算法构建的智能代理决策模块为例,考察市场在无约束排队出清方式下的情况.其中实验参数设置情形为:实验最大迭代轮数为600;发电厂商报价函数最大容量段数为 4;代理的策略集合设置参数情况为Si,min=1与Si,max=5,策略集中元素个数M=20;策略初始倾向系数设置为10000,各学习因子为ω=0.03,e=0.97,c=2000;代理的收敛阀值为δ=0.99.

实验各轮市场出清价格的变化见图 1,可以看出,代理经过 310轮左右的学习后,使市场处于一个稳定状态,市场出清电价也从开始的1.0元/(kW◦h)左右收敛到0.245元/(kW◦h).市场出清电价在前300轮竞价中波动剧烈,说明市场各发电厂商不断调整策略以期获得最大利润,使得市场竞争激烈;随后开始趋于平稳并逐渐收敛到市场实际边际成本附近,这说明经过反复竞争后,发电厂商最终基本按各自真实成本进行报价.算例表明代理学习算法可以模拟发电厂商在重复竞价过程中为获取自身最大收益而不断调整竞价策略的动态博弈过程,并且智能代理的学习过程最终使得市场出清电价收敛到边际成本附近,此现象在一定程度上符合完全竞争市场中的价格变化规律.

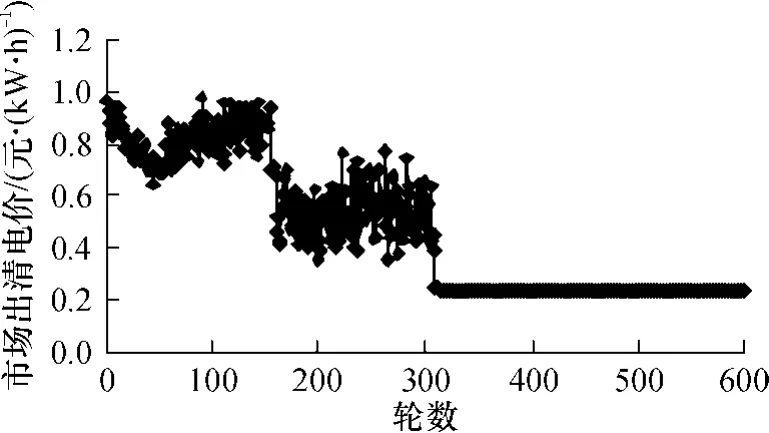
图1 市场出清电价变化Fig.1 Evolution ofmarket clearing price

通过该算例表明,智能代理模型及学习算法具有模拟仿真发电厂商追求利润这种理性行为的能力;适合用来构建模拟系统中的决策模块,同时是实现电力市场模拟系统智能化的重要工具,这对考察分析实际电力市场的运行具有重要的现实意义.

5 结语

电力市场模拟系统不仅是对电力市场进行深入量化分析的平台,而且也是分析制订市场规则与培训相关人员的重要工具.推进电力市场模拟系统的建设有助于我国电力市场的进一步深化改革.

为发电厂商构建基于智能代理及学习算法的决策模块是实现智能电力市场模拟系统的核心与关键.文中介绍运用的VRE learning算法、贪婪算法与Q-learning算法均从不同方面体现了发电厂商决策时的心理,在一定程度上体现了发电厂商竞价的理性行为.这些代理学习算法在电力市场模拟系统中的实现运用,为发电厂商的竞价提供了多样选择,实现了电力市场的智能仿真.

同时需要特别指出的是,电力市场基于智能代理模型仿真方法的研究还处于初始阶段,实验设计规则与仿真结果的分析方法等目前都还没有得到一个广泛认可的规范,这需要进一步的研究探索.

[1] 陈皓勇,王锡凡,王秀丽.基于Java的电力市场竞价实验平台设计,实现及应用 [J].电力系统自动化,2004, 28(17):22-26.

Chen Hao-yong,Wang Xi-fan,Wang Xiu-li.Design,imp lementation and app lication of a Java-based platform for electricitymarket auction experiments[J].Automation of Electric Power Systems,2004,28(17):22-26.

[2] 宋依群,高瞻.Agent技术在电力市场中的应用综述[J].电力系统及其自动化学报,2008,20(3):115-121.

Song Yi-qun,Gao Zhan.Survey on the application of Agent technology in electricitymarket[J].Proceedings of the CSUEPSA,2008,20(3):115-121.

[3] Bower J,Bunn D.Experimental analysis of the efficiency of uniform-price versus discriminatory auctions in the England and Wales electricity market[J].Journal of Econom ic Dynamics and Control,2001,25(4):561-592.

[4] Sun J,Tesfatsion L.Dynam ic testing of wholesale power market designs:an open-source agent-based framework [J].Computational Economics,2007,30(3):291-327.

[5] Power Systems Engineering Research Center(PSERC). Power web user'smanual version 2.7[R].[S.l.]:Cornell University,2001.

[6] Center for Energy,Environmental,and Econom ic Systems Analysis(CEEESA)Decision and Information Sciences Division.Electricity market comp lex adap tive system (EMCAS)user'smanual-version 2.0[R].[S.l.]:Argonne National Laboratory,2006.

[7] 王玉荣,魏萍.电力市场仿真和培训系统的设计及实现[J].电力系统自动化,2007,31(12):96-99.

Wang Yu-rong,Wei Ping.Design and Implementation of powermarket simu lation and training system[J].Automation of Electric Power Systems,2007,31(12):96-99.

[8] 薛禹胜,彭慧敏.电力市场与电力系统交互动态仿真设计[J].电力系统自动化,2006,30(23):14-20.

Xue Yu-sheng,Peng Hui-m in.Analysis and simu lation and interaction between electricitymarket and power system dynamics[J].Automation of Electric Power Systems, 2006,30(23):14-20.

[9] 杨尚宝.电力竞价上网智能决策支持系统 [J].电力自动化设备,2006,26(11):101-103.

Yang Shang-bao.Intelligentdecision support system for electricity bidding[J].Electric Power Automation Equipment,2006,26(11):101-103.

[10] 邹斌,李庆华,言茂松.电力拍卖市场的智能代理模拟模型[J].中国电机工程学报,2005,25(15):7-11.

Zou Bin,Li Qing-hua,Yan Mao-song.An agent-based simu lationmodel on pool-based electricity market using locationalmarginal price[J].Proceedings of the CSEE, 2005,25(15):7-11.

[11] 宋依群.电力市场的多代理模型 [J].中国电机工程学报,2005,25(8):80-83.

Song Yi-qun.Multi-agent model of electricity market [J].Proceedings of the CSEE,2005,25(8):80-83.

[12] 陈皓勇,杨彦,张尧.电力市场智能模拟中代理决策模块的实现[J].电力系统自动化,2008,32(20):12-16.

Chen Hao-yong,Yang Yan,Zhang Yao.Realization of decision-makingmodule in agent-based simu lation of power markets[J].Automation of Electric Power Systems, 2008,32(20):12-16.

[13] Russell S,Norvig P.Artificial intelligence:a modern approach[M].Englewood Cliffs,NJ:Prentice Hall,2003.

[14] Roth A E,Erev I.Learning in extensive-form games:experimental data and simple dynam ic models in the inter mediate term[J].Games Econom Behav,1995,8(1): 164-212.

[15] Watkins C JC H.Learning from delayed rewards[D]. University of Cambridge,1998.