基于神经网络和遗传算法的公差优化设计

赵 罡 王 超 于红亮

(北京航空航天大学 机械工程及自动化学院,北京 100191)

基于神经网络和遗传算法的公差优化设计

赵 罡 王 超 于红亮

(北京航空航天大学 机械工程及自动化学院,北京 100191)

针对产品制造中公差与成本之间高度非线性关系的特点,提出了一种综合神经网络与遗传算法进行公差优化的方法,该方法利用遗传算法在大范围解空间内采用概率搜索策略得到全局最优解且有较强鲁棒性的特点,以及神经网络解决高度非线性问题的优越性,首先利用神经网络对公差成本进行仿真,得到具有黑箱特点的公差成本函数关系;然后在公差分配中采用遗传算法,以总成本最小为目标函数,以满足装配公差要求和符合标准公差等级为约束条件进行优化;同时基于 VC和 Matlab开发了公差优化系统,以飞机舱门锁钩机构为对象进行了验证,并针对不同的公差成本及分配方法进行了对比.结果表明:采用神经网络与遗传算法综合分配的结果与传统方法相比具有较大的优越性.

公差成本关系;公差优化;神经网络;遗传算法

公差设计包括公差分析与公差综合两个部分.公差综合(tolerance synthesis)也叫公差分配(tolerance allocation),是指在保证产品装配技术要求下规定各组成环尺寸经济合理的公差[1].在进行公差分配时,需要综合考虑零件的产品功能、尺寸大小、几何形状、材料性能、现场设备、工艺方法与制造成本等多方面因素.因此,公差分配可以有多种不同的公差分配方案,是一个相当复杂的多解问题.

公差设计的发展已经经历了 1个多世纪,但直到 1978年,文献[2]中提出利用计算机辅助确定零件的几何形状、尺寸和形位公差的概念,用数学方程式来描述零件的几何形状,并以此来进行零件的尺寸和公差设计.从此计算机辅助公差设计(CAT,Computer Aided Tolerancing)得到了广泛的关注.1988年,文献[3]提出将公差需求从设计阶段传递到制造阶段的方法来解决工艺设计中的公差问题,由此掀起了 CAT研究的高潮,随后CAT的研究进入了大发展期.

在公差综合方面国内外学者已经进行了较多的研究.文献[4]提出了基于规则的综合,给出了各种常用的公差综合理论及方法;文献[5-6]提出了公差鲁棒设计和相应的确定性算法;文献[7]提出了基于 BP神经网络的成本-公差模型;文献[8]对加工质量进行了公差分配,并提出了一种基于遗传算法的方法.国内方面,文献[9]提出了基于装配成功率的公差优化设计方法;文献[10]提出了基于群集智能的产品公差优化设计方法,利用粒子群的方法进行多目标综合优化.

这些研究极大地拓展了 CAT研究的广度,但对于一些公差-成本关系复杂的模型来说,用传统的公差-成本模型来仿真拟合,然后再用构造的优化模型分配装配体中各个零件的公差量,其结果往往会误差很大,无法得到满意的优化结果;而把公差-成本模型与公差优化模型作为一体来综合考虑将会很好地解决这一问题.

考虑到公差优化是加工制造中的公差-成本模型及公差优化分配两部分的组合过程,本文提出将基于 BP神经网络和遗传算法结合在一起对公差进行优化分配的方法,并以飞机舱门锁钩机构作为实例对该方法进行了验证.

1 公差-成本模型

对于公差优化设计来说建立一个具有实用性的模型是至关重要的,因为模型对公差分配的实际应用起关键作用.由于各种零件的几何形状,尺寸及材料都有所不同,则其制造中所产生的成本也将不同,因此,一旦考虑到零件的加工材料、加工尺寸以及加工方法等,就很难用一个精确的数学模型来完整地描述公差与成本之间的关系.一般来讲,公差越小,所需要的加工成本便越大,反之则成本将越小.为了有效地表述公差与加工成本之间的关系,本文设定零件材料为铝合金,以中等批量零件加工时所用的切削用量和加工设备(主要是数控机床)为基准,以平面加工特征为研究对象,对公差及加工成本进行仿真.

1.1 传统公差-成本模型

对于公差成本模型的研究,已经有了大量的研究结果,提出了较多的公差-成本模型,如传统的指数模型、负平方模型、倒数幂指数模型等[7].这些模型的共同点是:在某特定的加工环境下,采集足够的公差成本的统计数据,然后用最小二乘法等优化方法确定模型中的参数.

但是,这些传统的公差-成本模型无法完整准确地描述公差成本之间复杂的数学关系.而神经网络方法在解决高度非线性问题方面具有很强的优越性,而且拟合误差可以控制在一个极小的范围,通过给定少量的训练样本作为输入和输出就可以很好地反映出输入输出间的关系.因此用神经网络来描述公差-成本模型就比较合适.

1.2 BP神经网络建立公差-成本模型

本文采用改进 LM(Levenberg-Marquardt)算法来训练 BP神经网络,从而模拟公差与成本之间的对应关系.基于 LM算法的 BP网络克服了BP算法随着迭代次数的增加,梯度下降逐渐变小,从而收敛速度较慢的问题,可以减少迭代次数,加速网络的收敛.

所需要确定的参数主要有:所用网络的层数、各层神经元的个数、各层的传输函数以及网络的学习算法.

1)网络的层数.研究[11]表明:如果 BP网络中隐层神经元数可以根据需要自由设定,那么一个 3层网络可以实现任意非线性映射.考虑到本模型对精度要求较高,因此采用含有输入层、隐层和输出层 3层的 BP神经网络.

2)各层神经元个数.一个具有无限个隐层神经元的 3层 BP网络可实现任意从输入到输出的非线性映射,但对于有限个从输入到输出的映射,并不需要无限个隐层节点.对于隐层节点个数的选择,至今为止,还没有找到一个很好的解析式,而是根据经验来确定节点个数,参数公式[11]为

其中,n为隐层节点个数;ni为输入节点的个数;no为输出节点的个数;a为 1～10之间的常数.

本文中输入节点为公差及其对应的工序类型,节点数为 2,输出为其对应的成本,节点数为1,得到隐层节点的个数为 n=10.

3)网络各层的传输函数.一般情况下,具有3层的 BP网络,隐层采用 Sigmoid类型的转换函数,而输出层则根据输出结果的范围选取,另外,为了在训练时能够使网络较快地达到稳定状态(即能够使网络的权值与阈值能够得到较快的调整),本文选取 tansig函数作为隐层传输函数,logsig作为输出层传输函数.为了提高训练速度和灵敏性及有效避开 Sigmoid函数的饱和区,需要对输入及输出数据进行归一化处理.由于生产过程中公差并不是均匀分布的,因此,本文对公差的归一化方法[8]为

其中,x为公差原始值;y为归一化之后的值.

4)系统模型.本系统所用的网络模型见图 1.

1.3 利用神经网络仿真

利用神经网络进行优化需要有对应的公差及成本数据作为专家样本来训练网络,而现实中工厂是以工序为单位进行生产,而以工时为单位来衡量成本的大小,公差与成本的数据难以统计,因此本文采用了文献[12]的数据作为优化用的样本数据.

基于 Matlab和 VC平台,开发了神经网络仿真公差-成本模型,其中 Matlab与 VC的混合编程的方式包括基于 MatCom,将 Matlab代码编译为dll或可执行程序,以及采用 Matlab Engine和Matlab的 C/C++数学库等 5种方法.

本文采用 VC调用 Matlab生成的动态 dll库的方法,通过将 Matlab神经网络工具箱的函数打包成 d ll然后在 VC里调用,图 2所示为对公差-成本的样本数据采用 BP网络进行训练的过程.

图1 公差-成本神经网络图

图2 VC调用Matlab进行神经网络训练

2 基于遗传算法的优化

其中,T∑表示封闭环的公差;n表示环的个数;Ti(i=1,2,…,n-1)表示各组成环的公差.

当 T∑ 已知,而 Ti未知时,式(3)为不定方程,有无数组解.考虑到不同的侧重,如加工精度、

2.1 传统分配方法

极值法情况下封闭环与组成环的公差关系为工序能力等,解决这个问题的传统方法有等公差法、等精度法、等工序能力法等.

这些传统的分配方法过于简单,只适用于公差设计初期,可得到简单的公差分配结果,而遗传算法不仅能收敛到全局最优解,而且具有较快的收敛速度,算法优化效率高,鲁棒性强,更适合于获得全局最优的公差分配结果.

2.2 遗传算法公差优化分配

本文需要优化的是各组成环的尺寸公差,在其满足标准公差等级的要求,同时还需要保证相应封闭环的技术要求的前提下,使得各组成环的加工成本最低,即

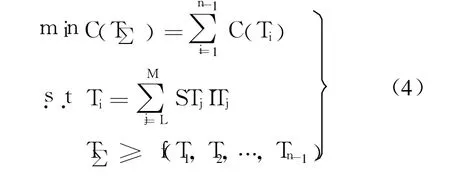
其中,ITj表示各组成环优化后的公差等级是否为IT j,如果所选取的等级为 j,则 ITj=1,否则,ITj=0;STj表示公差等级为 j时组成环对应的标准公差值;f(T1,T2,…,Tn-1)表示各组成环公差与封闭环公差之间的关系式,根据技术要求不同,其值也不同.在考虑装配成功率满足 6σ法则时:

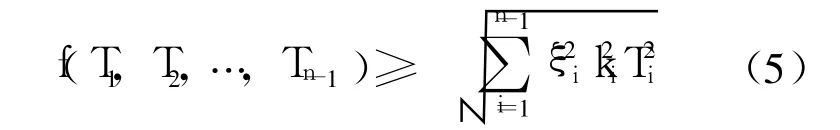
通过采用遗传算法,将标准公差等级编码,同时加入罚函数以表示相应的约束条件,将公差成本作为适应度函数值,可以较为方便地解决这一问题.

1)标准公差等级编码.编码就是将问题的解用一种码来表示,从而将问题的状态空间与 GA的码空间相对应.通过 GA搜索得到符合要求的最优解的编码而将其对应到问题的表现.研究[13]表明,采用二进制编码方案能包含最大的模式数,使得遗传算法在确定规模的群体中能够处理最多的模式.

本文采用二进制编码的方式,以各个组成环公差等级编号组合作为最后的编码.每个组成环公差等级编号由 3位二进制码组成.

总的编码长度为

总的编码方式为

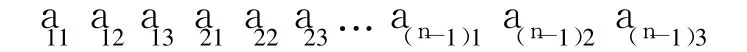
其可能的组合方式有 23×23×…×23=(23)(n-1)种.其中,每个组成环有 8种备选公差等级:IT 5～IT 12,于是一个具有 5个组成环的尺寸链,其个体的编码为,其中每个字符代表 0或 1,则一个编码为 011010000100的个体解码后所表示的意义如表 1所示.

表 1 个体解码的意义

2)约束条件的转换.根据式(4),本文中所要解决的问题包含 2个约束条件,针对这 2个约束条件,本文采用了 2种不同的处理方法:

①用编码的方法来保证产生出的个体总是在可行解空间之内.如针对公差等级 IT 4～IT 11共 8个等级,分别以 000～111予以对应.这样就解决了第 1个约束条件:

②通过加入罚函数的方法,降低不在解空间里的个体的适应度,从而降低该个体遗传到下一代群体中的概率.

其中,FC(x)表示修正之后的适应度函数;P(x)表示所选取的罚函数.

本文选取 P(x)=F(x)来作为罚函数,使得不满足要求的个体遗传到下一代群体中的概率为0,这样虽然降低了群体的多样性,但是却加快了算法的收敛速度.经实例验证,该方法设定罚函数是有效的.

2.3 系统工作流程

基于以上理论方法,采用 VC调用 Matlab生成的动态dll库的方法,开发了遗传算法优化公差的系统,在其中调用了神经网络优化得到的公差数值,完成了基于神经网络和遗传算法的公差优化设计.整个系统的工作流程如图 3所示.

图3 系统工作流程图

3 实例分析

3.1 实例说明

本实例以飞机舱门中锁钩机构的公差设计为研究对象,通过对其进行公差分配来验证所提出算法的可行性以及采用神经网络和遗传算法进行公差分配的优越性.图 4所示为舱门运动机构组件中锁轴和锁钩组件装配部分图,图 5为其对应的尺寸链.为了保证锁钩处于打开或者关闭状态都能够平滑地运动,需要检查锁钩与偏心衬套之间的间隙尺寸 A0.根据设计要求,间隙 A0应该在4.00～4.75mm范围内.

图4 舱门锁钩机构图

图5 相应的尺寸链

各零件的基本尺寸为:A1=A4=34.0mm,A2=28.5mm,A3=10.5mm,A5=111.0mm,对应的尺寸链方程为

以式(4)的总成本最小为目标函数.通过Matlab对公差成本以指数形式拟合,得到结果为

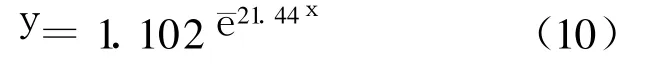
其拟合图像如图 6所示.

图6 拟合指数形式的公差成本曲线

3.2 实验结果对比

本文采用了神经网络和指数法分别得到的公差成本模型以及公差分配分别采用遗传算法和等公差法,以 3种方法组合为例:神经网络与遗传算法结合、神经网络与等公差法结合、指数法与等公差法结合.对所分配得到的公差和成本结果进行比较,采用 3种组合方法求得的公差值和总成本(归一化后)的数据结果如表 2所示.

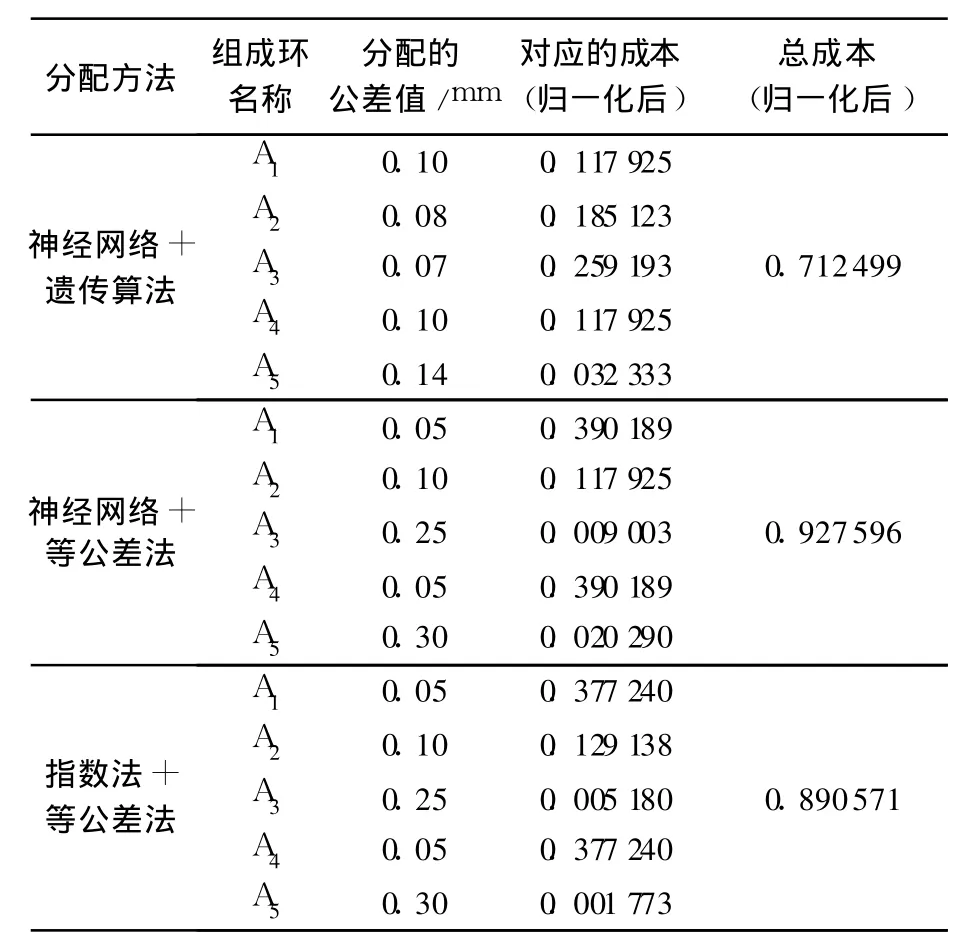
表 2 各种方法得到的公差值和成本对比

3.3 实验结果分析

由表 2的结果可知,采用遗传算法与神经网络结合的方法得到的总公差成本与其它 2种相比,分别降低了 30.189%和 24.993%,达到了较好的效果.

4 结 论

本文综合利用了神经网络与遗传算法各自的特点来解决公差优化中公差-成本关系和公差分配 2个问题.利用神经网络对公差成本进行仿真,得到具有黑箱特点的公差成本函数关系,在此基础上以最小成本为目标函数,以满足装配公差要求和标准公差为约束条件,利用遗传算法进行优化,并通过实例验证了该方法的可行性,结果表明,采用本方法进行公差分配可以明显降低产品的成本.

References)

[1]吴昭同.计算机辅助公差优化设计[M].杭州:浙江大学出版社,1999:3-6 Wu Zhaotong.Computer aided tolerance optimization design[M].Hangzhou:Zhejiang University Press,1999:3-6(in Chinese)

[2]Hillyard R C.Dimensions and tolerances in shape design[D].Cambridge:Computer Laboratory,University of Cambridge,1978

[3]Weill R,Clement R,Hocken R.Tolerancing for function[J].CIRP Annals-Manufacturing Technology,1988,37(2):603-610

[4]Raman S,PanchalK,SiminpulatP.Computer aided tolerance assignment[J].Computers＆Industrial Engineering,1991,21:67-71

[5]Parkinson D B.Robust design by variability optimization[J].Quality and Reliability Engineering International,1997,13:97-102

[6]Parkinson D B.The application of a robust design method to tolerancing[J].Journal of Mechanical Design:Transactions of the ASME,2000,122:149-154

[7]Lin Z C,Chang D Y.Cost-tolerance analysis model based on a neural networks method[J].International Journal of Production Research,2002,40(6):1429-1452

[8]Forouraghi B.Worst-case tolerance design and quality assurance via genetic algorithms[J].Journal of Optimization Theory and Applications,2002,113(2):251-268

[9]杨将新.基于装配成功率的公差优化设计系统研究[D].杭州:浙江大学机械工程学系,1996 Yang Jiangxin.Study on computer-aided tolerance optimum design based on stack-up yield[D].Hangzhou:Department of Mechanical Engineering,Zhejiang University,1996(in Chinese)

[10]肖人彬,陶振武,邹洪富.基于混合群集智能算法的并行公差优化设计[J].计算机集成制造系统,2007,13(4):668-674 Xiao Renbin,Tao Zhenwu,Zou Hongfu.Concurrent tolerance optimization design based on hybrid swarm intelligence algorithm[J].Computer Integrated Manufacturing Systems,2007,13(4):668-674(in Chinese)

[11]周开利,康耀红.神经网络模型及其 MATLAB仿真程序设计[M].北京:清华大学出版社,2005:75-94 Zhou Kaili,Kang Yaohong.Neuralnetworkmodel and MATLAB simulation programming dsign[M].Beijing:Tsinghua University Press,2005:75-94(in Chinese)

[12]杨将新,顾大强.基于神经网络的机械加工成本-公差模型[J].中国机械工程,1996,6:41-42 Yang Jiangxin,Gu Daqiang.Machining cost-tolerance model based on artifical neural network[J].China Mechanical Engineering,1996,6:41-42(in Chinese)

[13]周明,孙树栋.遗传算法原理及应用[M].北京:国防工业出版社,1999:32-40 Zhou Ming,Sun Shudong.The genetic algorithms:algorithms and applications[M].Beijing:National Defense Industry Press,1999:32-40(in Chinese)

(编 辑:文丽芳)

Tolerance optimization based on neural network and genetic algorithm

Zhao Gang Wang Chao Yu Hongliang

(School of Mechanical Engineering and Automation,Beijing University of Aeronautics and Astronautics,Beijing 100191,China)

Taking into account the highly non linear relationship between the cost and the tolerance in the product manufacturing process,a method based on the neural network in conjunction with the genetic algorithm was proposed to solve the tolerance optimal issues.The method integrates the advantage of the genetic algorithm,which can obtain the optimal result in a large-scale solution space using the probability searching strategy and the strong robustness,and the superiority of the neural net work that can solve the highly nonlinear problem.In the optimization process,the neural network was trained using sample data to simulate the tolerance-cost function at first and geta function relationship with the black box feature between the cost and the tolerance.And then the genetic algorithm was introduced to optimize the tolerance allocation by taking the results of the trained neural network.It takes the functional requirements and the standard tolerance grades as constraints as well as the minimum of the component cost as the objective.A tolerance optimization system based on a C++library and the Matlab was designed.Finally,an example of the latching shaft and hook mechanism component of the aircraft cargodoor demonstrated the method.The analytical result proves that the new method can produce the tolerance optimization economically and accurately,and has an advantage over traditional methods.

tolerance-cost function;tolerance optimization;neural network;genetic algorithm

TP 391

A

1001-5965(2010)05-0518-06

2009-12-15

国家 863计划资助项目(2007AA 041902)

赵 罡(1972-),男,河北文安人,副教授,zhaog@buaa.edu.cn.