基于灰色 GM(1,1)模型的城市工业用水量预测
2010-03-15郭法强
郭法强
(新疆宏昌水利规划设计公司,新疆乌鲁木齐 830000)
0 引言
城市用水量预测是进行城市建设规划、输配水系统优化调度的一项十分重要的前提工作。而城市中工业用水量占城市用水量的 2/3,其创造的效益更是其他行业无法比拟的,所以预测城市工业用水量,无论在经济效益还是在宏观调控上都有重要意义[1]。
国内外关于资源需求量预测方法主要有 3种,即时间系列预测法、弹性系数预测法和因果关系预测法。因果分析预测法是通过确定已知变量来预测未知变量的方法。同另两种预测方法相比,因果分析预测方法相对较简单,而且预测结果更精确。影响城市工业用水量的因素很多,其中一些因素是确定的,而一些因素则不确定,故可以把它看作一个“灰色系统”,可用时间序列观测值建立GM(1,1)模型[2,3]。
1 灰色预测模型 GM(1,1)[4,5]
1.1 原始数据处理
城市工业用水量的原始数据具有随机性,为了找出其中的内部规律,弱化原始数据的随机性,增强其规律性,可以借助累加(累减)生成的方法对其作必要的处理。
设某原始序列:X(0)={X(0)(1),X(0)(2),…,X(0)(n)}
对其进行一次累加生成,得到生成序列:

因为灰色 GM(1,1)模型实质为指数方程,要求用于预测的样本数据也要符合指数规律,因此,要进行序列的规律性检验。
(1)光滑性检验,若序列 X同时满足:
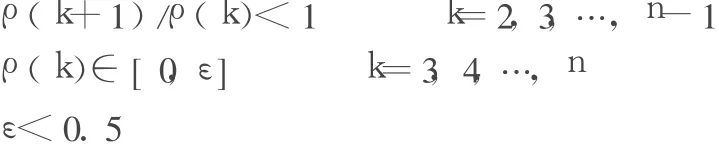
则称 X为准光滑序列。
式中:ρ(k)=X(0)(k)/X(0)(k-1),k=2,3,…,n,为序列 X的光滑比。
(2)指数规律性检验,若序列X同时满足:
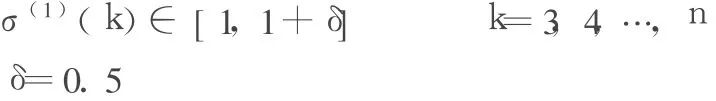
则称 X具有准指数规律。
式中:σ(1)(k)=X(1)(k)/X(1)(k-1),k=2,3,… ,n,为序列 X的级比。
一般情况下,对于非负的准光滑序列通过(一次)累加呈现出(准)指数规律,即可建立指数模型。
1.2 模型的建立
GM(1,1)模型是指一阶、一个变量的微分方程预测模型,是一阶单序列的线性动态模型,用于时间序列预测的是离散形式的微分方程模型。其具体形式是:

式中:α为发展灰数,α的可容区为(-2,2);μ为内生控制灰数。
1.3 αˆ为待估参数向量,可利用最小二乘法求解

求解微分方程,得预测模型:
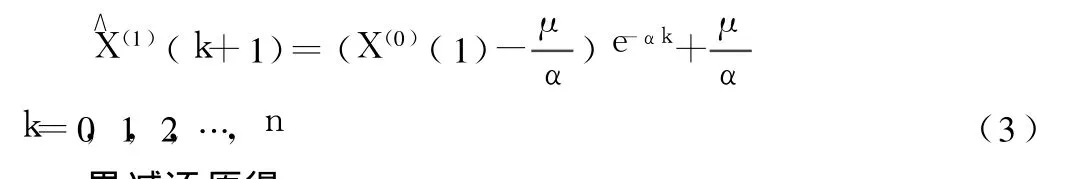
累减还原得:

式(3)、(4)即为 GM(1,1)模型进行灰色预测的基本计算公式。
1.4 模型残差检验和后验差检验
(1)残差检验
残差检验就是计算相对误差,以残差的大小来判断模型的好坏。
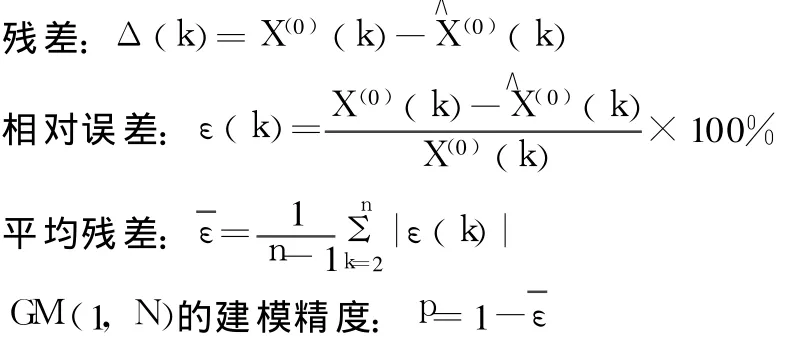
则 ε(k)越小越好,p越大越好,一般要求 ε(k)<20%,p>80%;最好是 ε(k)<10%,p>90%。X(0)为原始数列,X∧(0)是由式(6)得到的预测数据列。
(2)后验差检验
后验差比:C=S2/S1
式中:S1为原始数列 X0的均方差;S2为残差序列{Δ(k)}的均方差;C越小,模型越好。
2 应用举例
2.1 模型计算
以 1994~2000年抚顺地区工业用水量数据为原始序列(见表2 )。
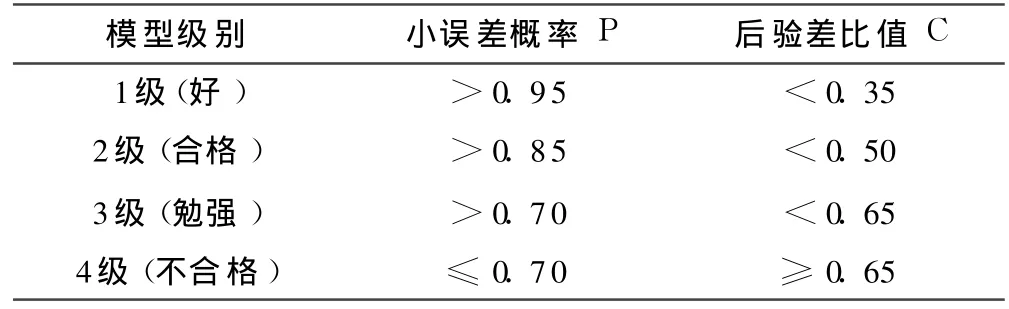
表1 检验指标等级标准

表2 抚顺地区工业用水量
依据灰色模型原理建立 GM(1,1)模型,并求得模型参数:a=-0.007 73,μ=5.135 331,最终得模型计算式为:
X∧(0)(k+1) =668.671 037e0.00773(k+1)-668.671 037e0.00773k
2.2 模型检验
(1)残差检验。经检验,模型相对误差值为 -2.73%~2.17%(见表3 )
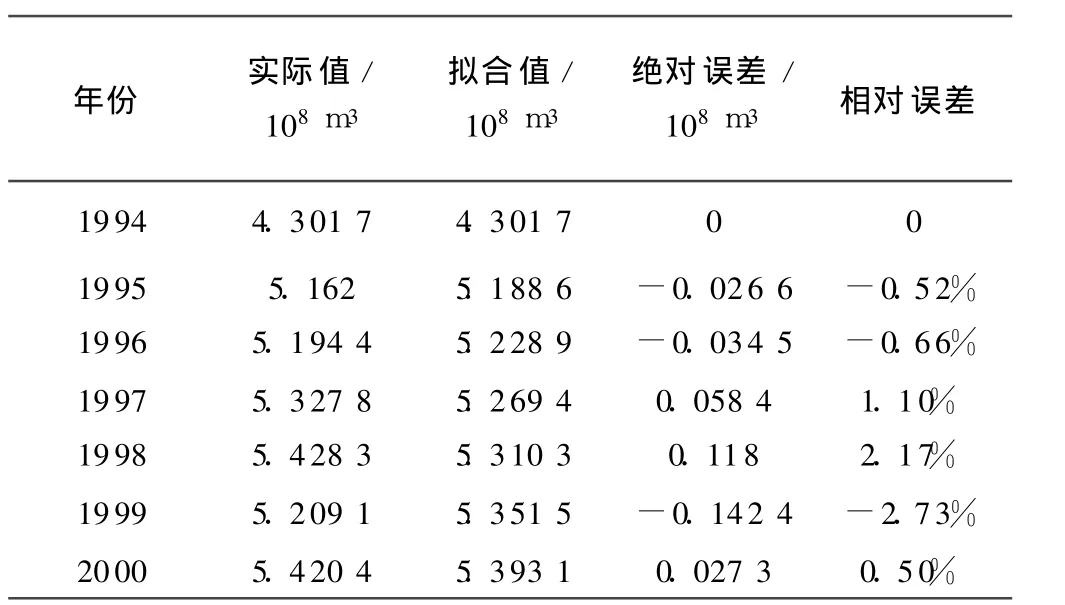
表3 模型拟合及误差计算
其残差平均值 ε=1.28% <10%,平均精度 p=98.72%>95%,模型拟合精度较高,模型判为优。
(2)后验差检验。经计算,后验差比值 C=0.227 5<0.35,小误差概率 P=1,模型级别为好。
模型拟合程度见图 1。

图1 模型计算值与实际值拟合
2.3 工业用水量预测
经过检验的模型符合精度要求后,可用于外推预测。2001~2004年抚顺地区工业用水量预测结果见表 4。
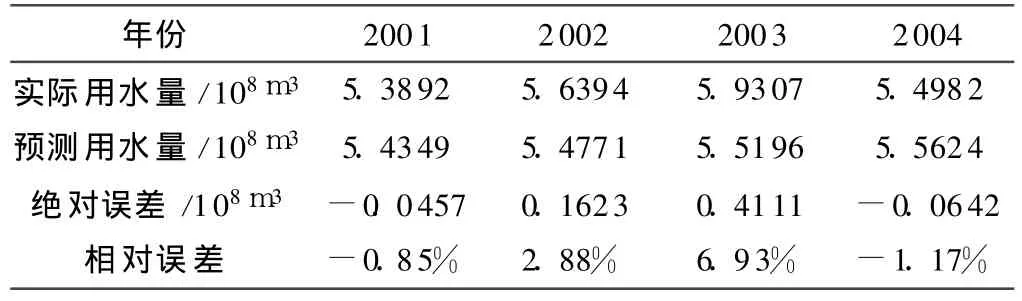
表4 2001~2004抚顺地区工业用水量预测
由表 4可知,模型预测相对误差分别为 -0.85%、2.88%、6.93%与 -1.17%,模型精度较高。
3 结语
根据灰色预测原理建立的工业用水量 GM(1,1)预测模型。经检验,平均精度达到 98%以上。由预测结果看,工业用水量呈缓慢上升趋势,与实际较吻合。随着地区经济的发展,城市工业化进程的加快,从而导致城市工业用水量呈增加趋势。
[1]宋巧娜,唐德善.城市工业用水量的灰色马尔科夫预测模型[J].中国农村水利水电,2007,(5):54-56.
[2]张雄.城市用水量预测模型综合研究[J].水资源与水工程学报 ,2005,16(4):24-28.
[3]邓聚龙.灰色预测与决策[M].武汉:华中理工学院出版社,1985:7-9.
[4]傅立.灰色系统理论及其应用[M].北京:科学技术文献出版社 ,1991:54-56.
[5]周刚,王弘宇,胡春雪,等.应用灰色新陈代谢 GM(1,1)模型预测中长期城市需水量[J].中国农村水利水电,2005,(8):16-18.
