基于有限元法的金属材料静强度破坏准则应用研究
2010-03-15刘洋周柏卓
刘洋,周柏卓
(沈阳发动机设计研究所,沈阳110015)
1 引言
在传统航空发动机强度设计中,主要采用一些解析、半解析解法或经验分析方法进行静强度计算分析,通过经验方法定出安全系数,从而确定静强度破坏载荷。这样的强度设计方法基本能够满足工程需要,但是手工计算量大、精度较低。有限元法已经成为现代航空发动机强度设计中所采用的主要方法。但到目前为止,由于有限元结果没有1个有效的静强度评价标准,无法通过计算结果预知结构能承受的最大静载,因此,亟需建立1种满足工程需要的有限元静强度评价标准。
本文根据1种基于有限元法的金属材料静强度破坏准则(根据此准则,可用光滑试件的短时力学性能较精确预测出缺口试件的短时力学性能[1-3],此准则在预测航空发动机轮盘破裂转速上同样得到了较精确的结果[2,3]),设计了2种试验件,计算了破坏载荷,并通过了试验验证。
2 缺口拉伸试样的设计目的
基于有限元法的金属材料静强度破坏准则可表述为:在静载荷作用下,当结构内任意1局部点的当量对数塑性应变达ln(3-2)时,结构的这一点亦破坏,此时结构亦破坏。其中ψ为材料的断面收缩率。
本文基于上述准则,设计了2种ZTC4的材料试验件,如图1、2所示。2种试样除缺口部分外完全相同,缺口的半径也相同,因此2种试件的净截面积相同。利用常规方法作为静强度的分析手段,通过计算得知2种试样所能承受的破坏载荷完全相同。根据非线性有限元的计算分析以及相应的破坏准则可知,2种试件所能承受的破坏载荷是不同的,这一结论也得到了试验验证。通过2种试件的拉伸试验证明了常规方法的局限性,同时也验证了基于有限元法的金属材料静强度破坏准则的合理性。
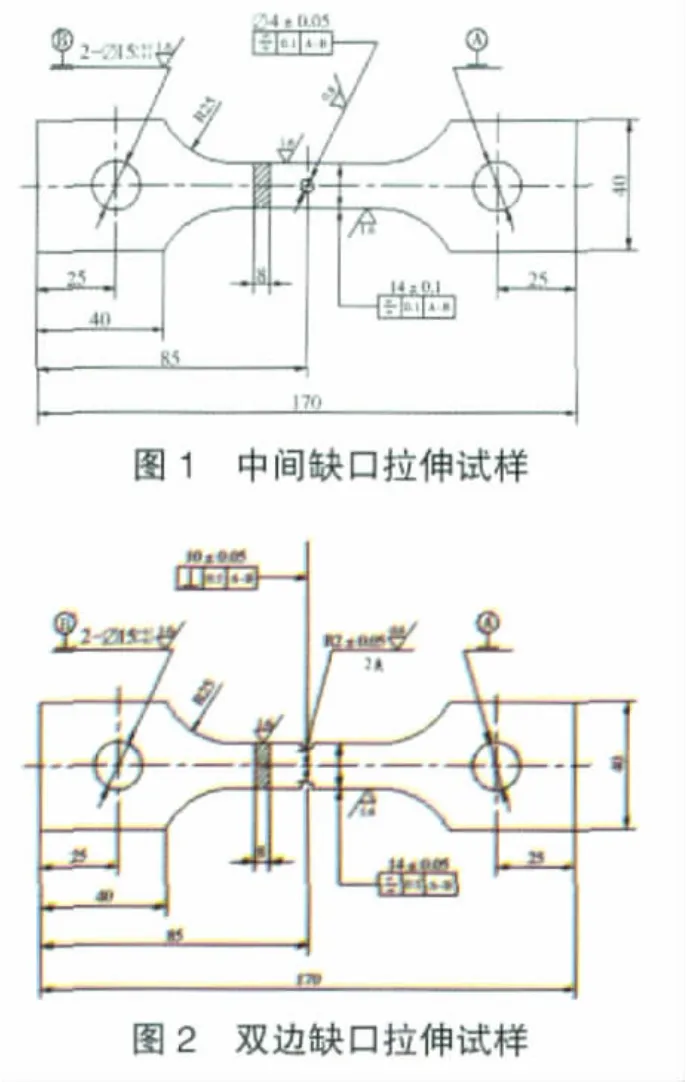
3 缺口试样的有限元模型
对于同等规模的有限元模型,非线性有限元分析与线弹性有限元分析相比,需要耗费更多的计算时间;为了使试样的有限元模型足够精细,以便更精确地模拟实际试样,需要划分尽可能多的单元。本文利用试样结构以及加载方式的对称性,取试样的1/8进行分析(根据对称性,取试样的1/4,再取厚度的1/2),使计算规模和精度达到了很好地平衡。
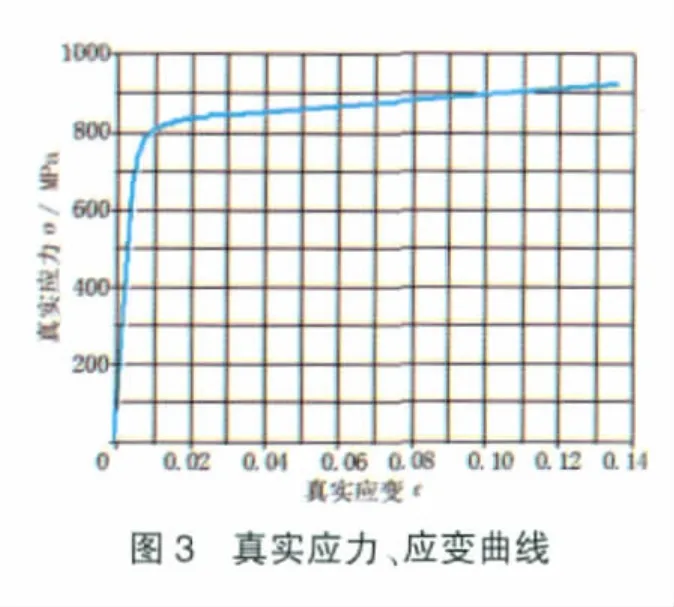
在试样的有限元模型中所有的对称面施加对称边界条件,在试样两端的圆孔位置建立梁单元模拟加载销子对试样的拉伸作用。试样材料ZTC4的材料性能数据由来自同一毛坯的标准件拉伸试验确定,弹性模量E为113.3 GPa,泊松比为0.267,ψ为0.14,实测的真实应力、应变曲线如图3所示。
4 计算结果
由图3及破坏准则可知,当取自ZTC4毛坯的典型试样的当量对数塑性应变达到0.136时,试样即发生破坏。由于各级载荷步的当量塑性应变与实际破坏的当量塑性应变稍有差别,因此取最接近破坏时的载荷步的当量塑性应变。
中间缺口拉伸试样(试样1)和双边缺口拉伸试样(试样2)接近破坏载荷步的当量塑性应变、当量应力的分布规律如图4~7所示。根据加载位置的反力,可算出破坏载荷。由结构的对称性可知,当达到破坏载荷时间步长时,加载点反力的4倍即为破坏载荷。破坏载荷见表1。


表1 试样的计算破坏载荷
5 缺口拉伸试样的试验结果
为了与上面计算得到的非线性有限元结果进行对比分析,进行了缺口试样的拉伸试验。图8列出了试样1和试样2的外载荷随试验机夹头位移的变化曲线(试样1和试样2各有4件,因为仪器记录问题,有2件试样2的试验曲线数据丢失,图中曲线1~4来自试样1,曲线5、6来自试样2)。试样破坏载荷的平均值见表2,通过与表1对比,列出了计算结果误差。

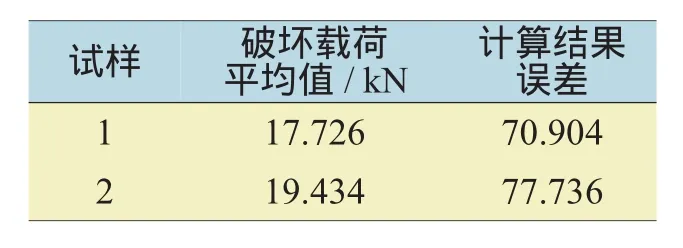
表2 试样的破坏载荷及计算误差

图9为试验过程中试样1和试样2的实时照片。其中图(a)、(c)是试样开始拉伸时缺口部位形态,图(b)、(d)是断裂前瞬间缺口部位形态。从断裂前缺口形态图可见,拉伸使得缺口周围形成了较明显的塑性变形。
6 计算与试验结果的对比分析
计算结果中未列出外载荷随位移的变化曲线。原因在于,图8中的位移包含加载设备位移,试验得到的位移与计算得到的位移没有可比性。
由图4、6中可见,计算得到试样的破坏位置在缺口部位。这在图9中体现得很明显,与有限元计算结果符合得很好。从试件1拉断后的断口来看,一般是从塑性应变最大位置开始起裂,沿近似45°方向扩展;从图5中可见,最大当量应力是沿近似45°方向分布的,因此计算结果与试验符合得很好。
7 结论
按常规静强度评价标准,试样1和试样2的破坏载荷是完全相同的;但是从本文的计算和试验中可见,二者破坏载荷相差约12.5%。非线性有限元计算得到的破坏载荷与试验结果相比,误差很小,很好地验证了基于有限元法的金属材料静强度破坏准则。
[1] 周柏卓,万江艳.试件短时力学行为的非线性有限元方法描述[J].材料工程(增刊1),2006(10).
[2] 万江艳,周柏卓.轮盘破裂转速的弹塑性、大应变有限元分析方法[J].材料工程(增刊1),2006(10).
[3] 万江艳.轮盘破裂的非线性有限元分析方法及试验验证[D].沈阳:沈阳发动机设计研究所,2007.
[4] 陈火红.MSC.Marc/Mentat 2003基础与应用实例[M].北京:科学出版社,2004.
