温度分布对自由盘层流换热的影响

吕品，王成明，赵熙，徐国强

（北京航空航天大学能源与动力工程学院，北京100191）

1 引言

自由盘是指在无限大空间里以一定角速度旋转的圆盘，远离转盘的流体静止，研究自由盘的流动和换热是研究实际发动机中复杂盘腔内流动和换热的基础，如在某些情况下，转静系旋转盘腔可简化成自由盘[1]。

对自由盘层流流动，Von karman[2]通过相似变换，将控制自由盘附近流体流动的偏微分方程转化为常微分方程并求解，得到自由盘的局部流量系数和盘面单侧力矩系数；对盘面换热，给定盘面过余温度n（Tw为盘面温度、Tf为主流温度）的情况下，Dorfman[3]、Owen[4]通过积分求解能量方程分别得到盘面局部努赛尔数。对自由盘的湍流流动，Von karman[2]、Dorfman[5]、Owen[4]分别采用理论推导和实验测量的方法，得到了盘面的流量系数和力矩系数；对盘面换热而言，给定盘面温度边界条件Tw-Tf=Crn，Dorfman[6]基于对数律所求出的速度场来求解能量积分方程，得到自由盘盘面的局部和平均努赛尔数。

根据以上经典研究结果可知，自由盘盘面的换热在一定程度上受温度边界条件的影响，如当盘面过余温度按n次单项式Tw-Tf=Crn分布时，盘面局部和平均努赛尔数要受到指数n的影响。对于盘面过余温度按一般化的n次多项式Tw-Tf=a0+a1r+a2r2+…+anrn分布时，盘面换热结果在以上研究中没有给出，本文通过数值方法对此进行了探讨。

2 计算方法简介

采用静止坐标系下不可压缩流的控制方程描述问题[7]，能量方程中忽略了压力功及耗散项；各方程的离散采用2阶迎风格式，压力与速度的耦合采用SIMPLE算法。

2.1 计算模型及网格

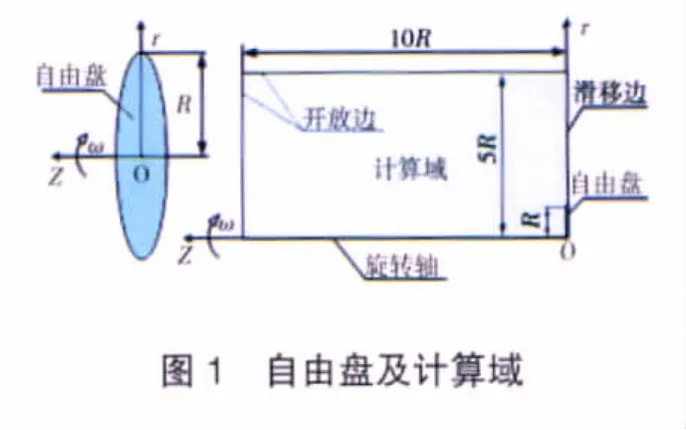
计算模型为Tw-Tf=Cf(x)，C=0.2 m的自由盘，仅计算自由盘单侧的流体域，如图1所示。旋转轴为z轴，计算域沿轴向范围为10 R，沿径向范围为5 R；由于流体域的轴对称特性，为节省计算资源可仅计算r-z截面的2维区域。计算网格采用正交4边形网格，2坐标方向的网格数目r×z约为140×200；由于自由盘附近流体速度及温度梯度较大，故对盘面附近网格进行加密。

2.2 物性及边界条件

物性条件：流体为不可压缩空气，在开放边处（如图1所示），流体温度Tf=300 K，并取此温度下的物性参数，密度ρ=1.185 kg/m3、定压比热容Cp=1004.4 J/(kg·K)、黏度μ=1.831×10-5kg/(m·s)、导热系数λ=0.0261 W/(m·K)。

边界条件：（1）自由盘，盘面为无滑移条件并给定盘面转速，自由盘层流向湍流过渡的临界旋转雷诺数Reω,c=ρπωR2/(30μ)=2×105[1]，R=0.2 m时对应的临界转速ωc≈740 r/min，故设置层流自由盘转速ω=300、500、700 r/min，对应旋转雷诺数分别为Reω≈0.813×105、1.355×105、1.898×105；盘面温度为Tw，盘面过余温度Tw-Tf=Crn或Tw-Tf=a0+a1r+a2r2+…+anrn，其中Tf为开放边流体温度，C为常数，指数n=0、1、2、3。（2）滑移边，边界上为无穿透、自由滑移、绝热条件。（3）开放边，给定压力Pf=1.01×105

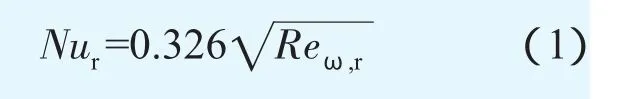
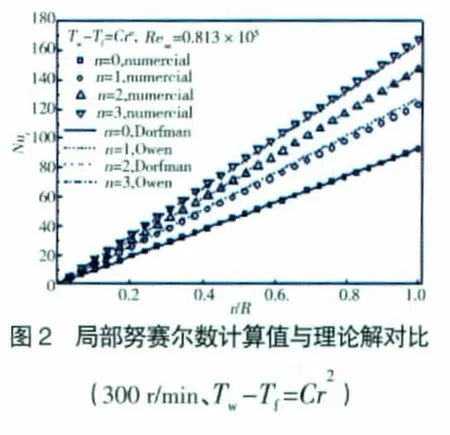
盘面过余温度Tw-Tf=Cr2（n=2）时

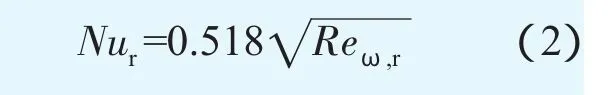
而对于任意Pr，当盘面过余温度为半径的n次曲线分布Tw-Tf=Crn时，Owen[4]得到的结果为

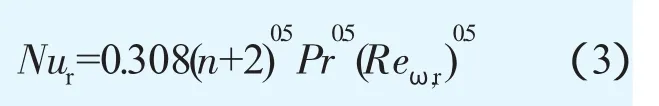
式中:局部努赛尔数Nur=hrr/λ;hr=qw/(Tw-Tf)为盘面局部对流换热系数;qw为盘面局部热流密度；局部旋转雷诺数Reω,r=ρπωr2/(30μ)。

由理论解可以看到，盘面的换热只受到指数n影响而与系数C没有关系。需要注意的是，式（1）、（2）为精确解；式（3）则为综合值，在0.71＜Pr＜2和0＜n＜3时，与精确解相比,最大误差为12.6%。

同样采用不可压缩、常物性假设和相同的边界条件后，利用此计算程序对前述的自由盘进行数值计算，得到了盘面局部努赛尔数Nur随无量纲半径r/R的分布，如图2所示。由图中可见，计算结果在n=0、2时与Dorfman的Pa（Pf在开放边入流时为总压，出流时为静压）；给定温度Tf=300K。（4）旋转轴，z轴为旋转轴，该轴上径向、切向速度均为0，轴向速度和温度沿半径的梯度也为0。

2.3 计算程序验证

对于自由盘盘面的换热，1963年Dorfman[3]通过积分求解不可压缩、常物性能量方程得到盘面局部努赛尔数的理论解。给定普朗特数Pr=0.72，盘面温度为常数C（n=0）时精确理论解符合很好，最大误差约为1%；而n=1、3时与Owen的综合解偏差稍大，最大在5%左右，这是由于Owen的结果为综合近似解而并非精确解所致。

3 计算结果分析

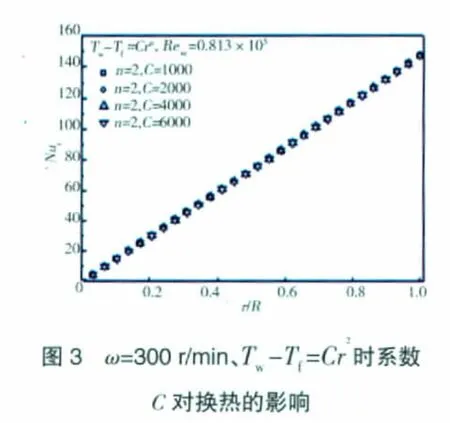
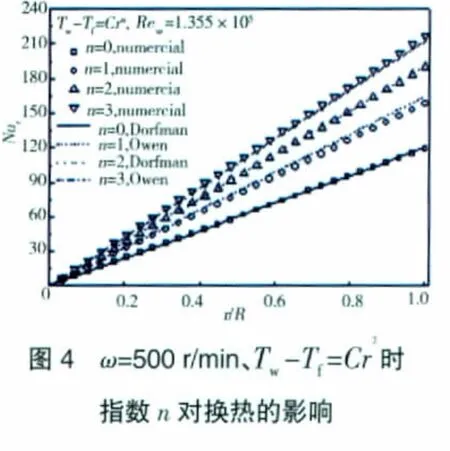
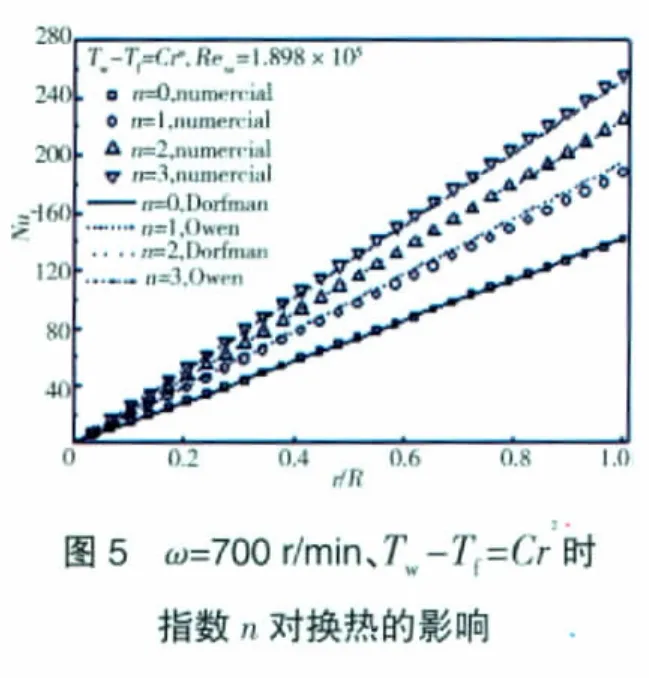
Tw-Tf=Cr2时系数C对盘面换热的影响如图3所示。从图中可见，局部努赛尔数Nur不随系数C改变，这与理论解的结论一致。图4、5给出了2个转速下盘面局部努赛尔数随盘面温度分布的变化情况，并与理论解进行了对比，二者符合较好。图中n=0、2时的Dorfman理论解分别由式（1）、（2）得到，而n=1、3时的Owen理论解则皆由式（3）得到。很明显，局部努赛尔数均随半径呈直线分布，这说明此时盘面的换热系数为常数，不随半径变化。理论解和数值结果均表明，n=2时的局部努赛尔数比n=0时的约大59%；计算结果中，n=1时的局部努赛尔数比n=0时的约大32%，n=3时的局部努赛尔数比n=0时的约大81%。

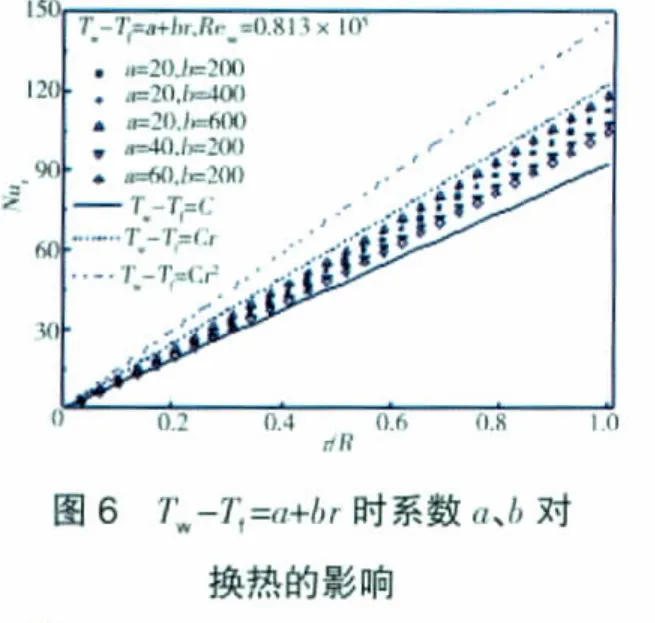
自由盘面温度分布为Tw-Tf=a+br时系数a、b分别对自由盘面局部努赛尔数的影响如图6所示。从图中可见，局部努赛尔数Nur随系数a的增大而减小，随b的增大而增大。值得注意的是，所得的局部努赛尔数，数值上位于盘面分别按最高1次（Tw-Tf=br）和最低0次（Tw-Tf=a）分布时所得的局部努赛尔数之间。

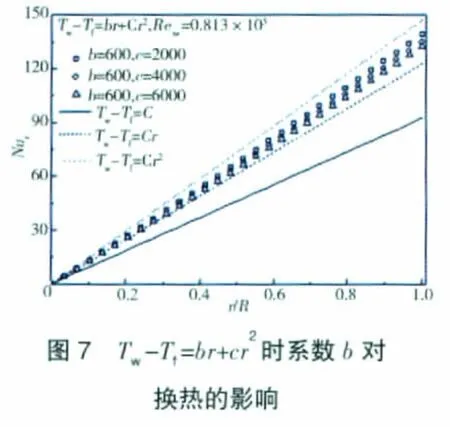
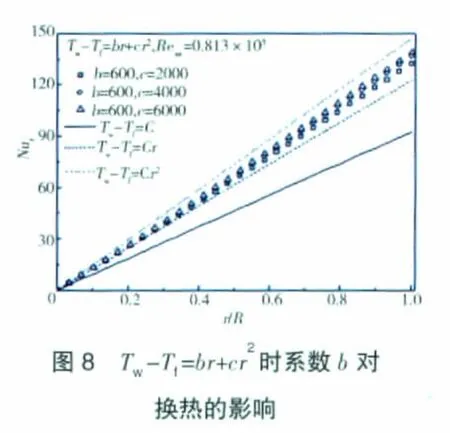
自由盘面温度分布为Tw-Tf=br+cr2时的自由盘面局部努赛尔数如图7、8所示。从2图中可见，局部努赛尔数b随最低1次系数b增大而减小，随最高2次系数c增大而增大；同样，所得局部努赛尔数数值上介于自由盘面分别按最高次（Tw-Tf=Cr2）和最低次cr2分布时所得的局部努赛尔数之间。

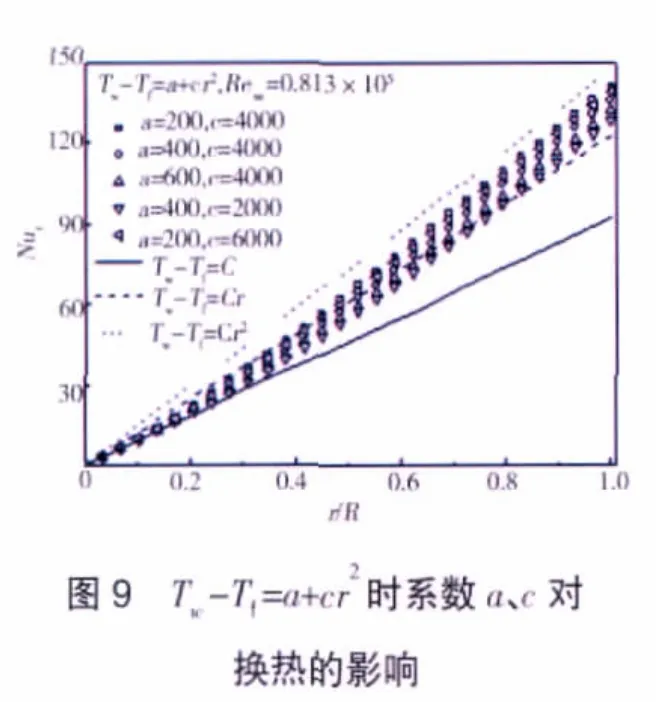
自由盘面温度分布为Tw-Tf=a+cr2时的盘面局部努赛尔数如图9所示。局部努赛尔数Nur随最低0次系数a的增大而减小，随最高2次系数c的增大而增大；计算所得的局部努赛尔数介于自由盘面分别按最高次Tw-Tf=cr2和最低次（Tw-Tf=a）分布时所得的局部努赛尔数之间。从图中可见，此时的局部努赛尔数曲线的形状发生改变，不再是直线，说明此时自由盘面的换热关系式不再满足成比例的关系，也即盘面换热系数不再为常数。

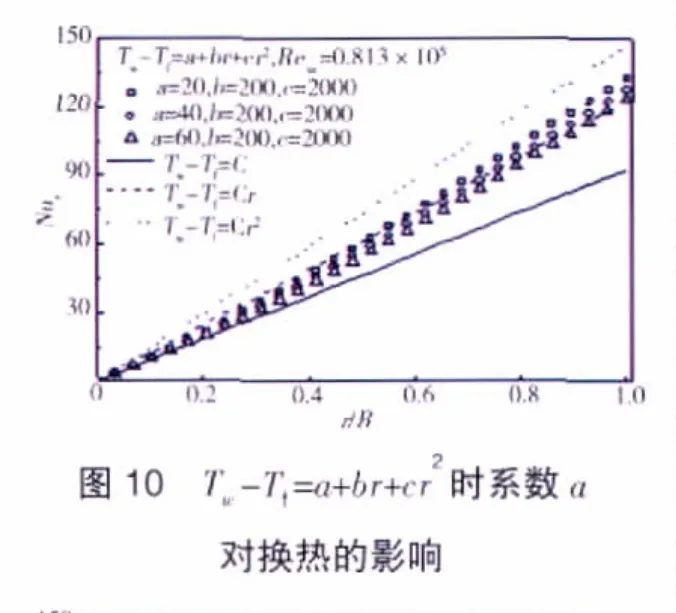
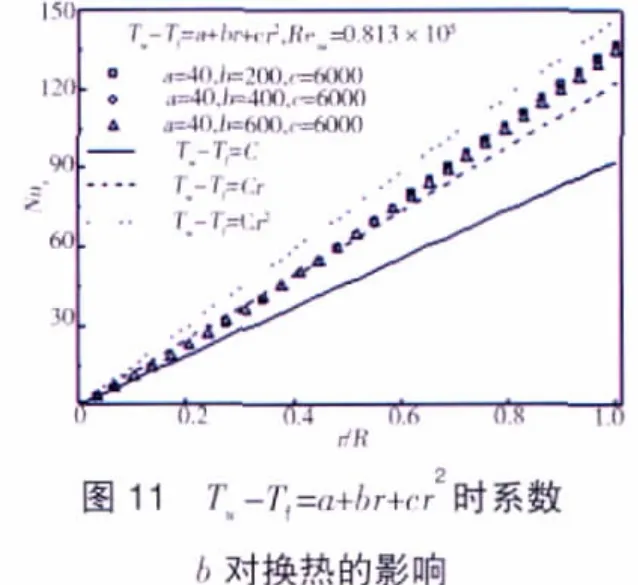
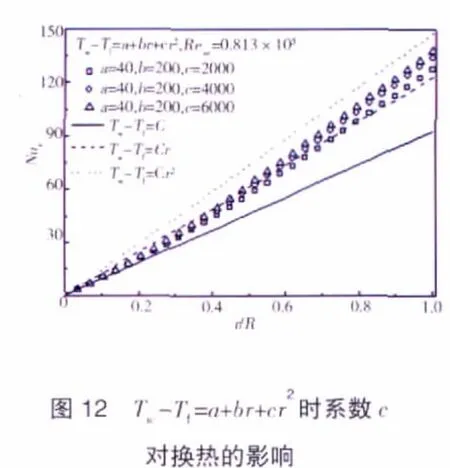
自由盘面温度分布为Tw-Tf=a+brcr2时系数a、b、c对自由盘面局部努赛尔数的影响如图10～12所示。从图中可见与前面相似的情形，盘面局部努赛尔数Nur随最低0次系数a的增大而减小，随最高2次系数c的增大而增大。系数b对局部努赛尔数的影响则分为2个区域，r较小时2次项cr2的影响较小，随着1次项系数b的增大，1次项在温度分布中占主导地位，b可近似认为是最高次项系数，故随着b的增大，自由盘面局部努赛尔数增大；另外，在r值较大区域，由于2次项在温度分布中的影响增大，1次项影响减小，故随着b的增大，局部努赛尔数减小。计算所得局部努赛尔数介于自由盘面分别按最高次（Tw-Tf=cr2）和最低次（Tw-Tf=a）分布时所得的局部努赛尔数之间，不再满足与成比例的关系。

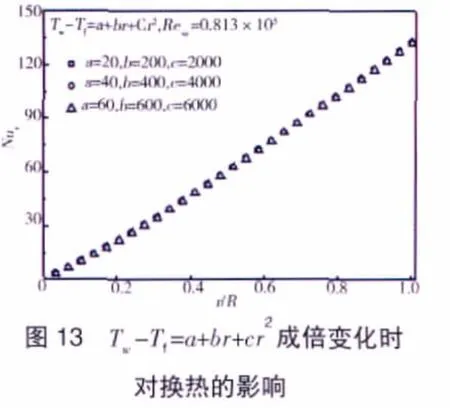
在不同温度分布下，当过余温度Tw-Tf成倍变化（即Tw-Tf=Cf(x)，C任意变化）时对自由盘面局部努赛尔数分布的影响如图13所示。由图中可以明显看出，温差Tw-Tf成倍变化时，自由盘面局部努赛尔数不发生改变（即不随C的改变而改变）。事实上这与自由盘面温度分布为Tw-Tf=C、Tw-Tf=Crn时自由盘面局部努赛尔数不随常数C改变而改变的结论相一致。

设盘面过余温度为n次单项式Tw-Tf=Crn分布，且当n为0、1、2、…、n时，盘面所得的局部努赛尔数分别为Nur,0、Nur,1、Nur,2、…、Nur,n定义局部努赛尔数之比

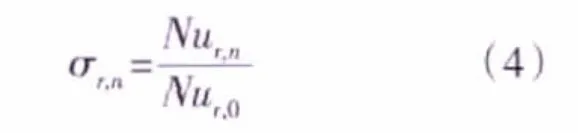
通过对以上数据综合分析发现：对自由盘层流换热，当盘面过余温度按任意多项式分布时，即

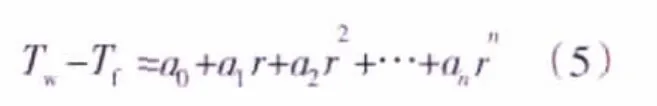
与流体外掠平板时表面换热的结果类似[8]，自由盘面局部努赛尔数Nur可由下式计算

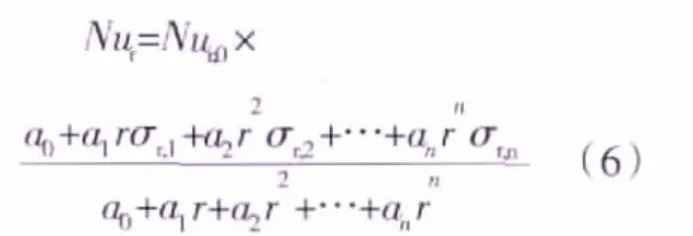
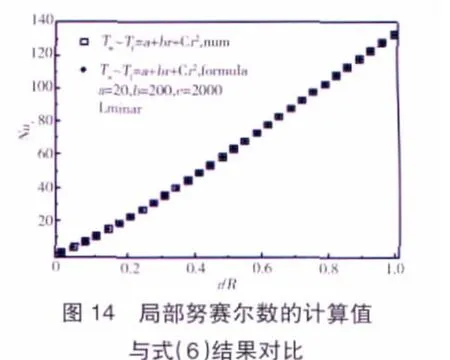
图14给出了过余温度按2次多项式分布时，盘面局部努赛尔数由式（6）计算的结果与数值模拟所得结果的比较。由图中可以看到，二者符合极好，表明了使用式（6）计算盘面过余温度按n次多项式分布时的局部努赛尔数的准确性。

4 结论

对不可压缩、常物性层流流动的自由盘:（1）当盘面过余温度Tw-Tf=a0+a1r+a2r2+…+anrn按任意多项式分布时，盘面局部努赛尔数数值上介于过余温度单独按多项式的最高次和最低次分布所得到的局部努赛尔数之间，且随最高次项系数的增大而增大、随最低次项系数的增大而减小、随着中间次数项的系数在低半径区域增大而增大在高半径区域增大而减小；（2）当Tw-Tf=Cf(r)时，盘面的换热不受系数C的影响；（3）当Tw-Tf=Crn时，局部努赛尔数在所有同次多项式温度分布下所得局部努赛尔数中为最大值；（4）当过余温度为半径的任意多项式分布Tw-Tf=a0+a1r+a2r2+…+anrn时，盘面局部努赛尔数可由式（6）计算得到。

[1] 曹玉璋,陶智,徐国强,等.航空发动机传热学[M].北京：北京航空航天大学出版社,2005.

[2] Karman Th,Von..Uber Laminare and Turbulence Rei-bung[M].Z angew.Math.Mech.,1921,1:233-252.

[3] Dorfman L,A,Translated by Kemmer N.Hydrody-namic Resistance and the Heat Loss of Rotating Solids[M].Oliver and Boyd Ltd.,1963.

[4] Owen J M,Rogers R H.Flow and Heat Transfer in Rotating-Disc Systems Rotor-Stator Systems[M].Research Studies Press,Taunton,UK,1989.

[5] Dorfman LA.Turbulent Boundary Layer on a Rotating Disc[M].Izv.Akad.Nauk SSSR,Otd.tekh.nauk,1957,no.7:138-142.

[6] Dorfman L A.Heat Transfer from Rotating Disc[J].Inzh.-fiz.Zh.,1958,1(6):3-11.

[7] 陈懋章.粘性流体动力学基础[M].北京：高等教育出版社,2002.

[8] Eckert E R G,Drake R M.Analysis of Heat and Mass Transfer[M].McGraw-Hill,1972.