关键链项目管理缓冲区计算方法研究
2010-03-12曹小琳刘仁海
曹小琳,刘仁海
(重庆大学 建设管理与房地产学院,重庆 400045)
0 引言
关键链项目管理(CCPM)技术是约束理论在项目管理中的应用和发展。关键链技术着眼于整体而非单个工序安全,采用风险聚合的原理剥离各活动的安全时间,形成多种缓冲(项目缓冲,输入缓冲和资源缓冲),将缓冲集中置于项目的特殊位置来抵消因各种原因造成的随机延误,从而保护项目能够按期完成。相关理论研究和实际应用证明[1-3],运用关键链项目管理技术能够在没有增加项目整体完工风险的条件下,大大缩短项目的计划工期。随着研究的逐渐深入,CCPM技术在项目组合管理[4]、资源调配[5]、风险管理[6]等方面都获得了成功应用。关键链技术通过引入缓冲机制来消除不确定性因素对项目调度计划的影响,保护关键链,因此正确的进行缓冲估计和设置是CCPM技术运用成功的关键。然而,目前尚无统一的、科学合理地确定关键链缓冲区大小的方法,论文对目前几种主要的关键链缓冲区计算方法进行比较分析与评价,并根据分析结果提出关键链缓冲区计算的新方法。
1 关键链缓冲区计算研究现状
1.1 缓冲区基本计算方法
根据目前国内外研究[7-9],缓冲区计算采用的基本方法有50%法和根方差法两种。50%法也被称作剪贴法 (Cut and Paste Met hod,C&P),采用链路上工序的安全缓冲Δti(Goldrat t[7]认为Δti等于工序工期估计的一半)的一半作为缓冲的大小,即:

其中:ΔB为缓冲区大小,Δti为工序的安全缓冲,n为对应链路上的工序数。
50%法计算简便,但主观性太强,将工序工期减一半缺乏科学性,而且缓冲区大小与累计安全时间成线性关系,随着不同项目工序数的不同,容易造成缓冲区过大或者过小的现象。
根据关键链理论,项目工期由关键链上工序工期构成,而各工序工期服从一定的概率分布,其分布的特征值表现为工序的均值和方差。文献[8]认为工序的安全缓冲Δti代表了工序工期的不确定性,提出用Δti/2作为工序工期的标准差,并以2倍的链路标准差作为链路的缓冲估计,这就是根方差(Root Square Error,RSE)法。
假定链路上工序工期相互独立,则根据中心极限定理可得:

对比上述两种计算方法,文献[10]认为根方差法建立在中心极限定理基础上,只有当链路上工序较多时,中心极限定理的作用才更明显,因此,对于大型项目,链路工序较多时,根方差法比50%法更为适用。杨立熙等[11]通过仿真模拟试验显示,随着链路工序数的增大,根方差法的项目计划工期从最初的大于50%法逐步发展为小于50%法,同时随着工序数增加,50%法的项目完工保证率逐步提高,而根方差法在逐步降低后趋于稳定。工序数大的情形下50%法计算过于保守,而根方差法却过于乐观,工序数中等的情形下两种方法计算的缓冲都未达到有效保证较高完工保证率的水平。
1.2 考虑资源约束的项目缓冲计算方法
由于50%法对不同项目采取相同的缓冲计算方法,根方差法则仅以工序持续时间的不确定性为主要依据计算缓冲大小,两种方法都没有充分考虑到缓冲加入后,新产生的资源冲突问题,以及项目中不同活动对于整个项目工期的不同影响。因此,马力等[12]提出一种基于根方差法的改进型自适应缓冲计算方法,在设置缓冲区大小时,考虑到了项目的相关属性参数,主要是项目中每个活动的资源利用程度,来进行缓冲设置。文献[12]认为资源利用程度可表示为某项活动所需的某种资源量占该资源可用资源总量的比例。在项目执行过程中,如果项目中某个工序的资源需求数量越接近于该资源的总供给量,该活动出现延迟的概率就越大,需要设置的缓冲就应该越长。对于项目中的某资源k与某工序i,资源利用程度为:
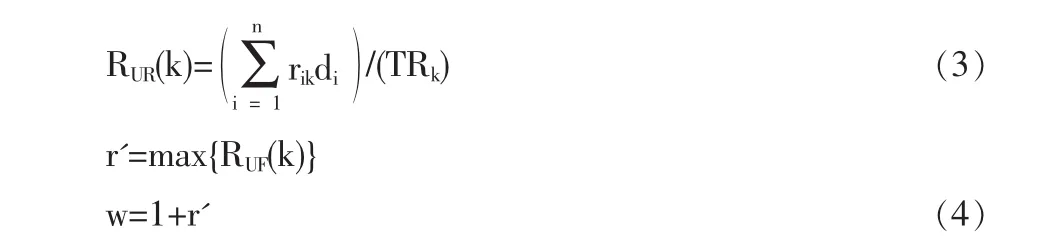
其中,rik为工序i对资源k的需求量,Rk为资源k的可用量;di为工序i的工期;T为对应链路的长度。
根据中心极限定理,对于链路上工序集合Jcc中的每一个工序i的工期方差σi求和可得:

相应的缓冲尺寸为:

1.3 考虑工序复杂度和风险偏好的缓冲计算方法
虽然文献[12]认为缓冲大小与活动相关属性参数有关,但是在计算的时候仅考虑了资源利用属性的影响。而Shou YY[13]等经过研究认为,缓冲的大小与项目的特点、性质以及项目利益相关者的风险偏好等因素有关。因此褚春超[14]提出了一种综合考虑项目资源紧张度、链路结构复杂度和管理者风险偏好等因素的缓冲计算方法,工序所用资源越紧张,链路结构越复杂,管理者要求的完工风险越低,相应的缓冲应该越大。
(1)资源紧张度αi
用αi表示工序i的资源紧张程度,有:

其中,Rt为项目在t时段的资源供应限量,rkt为在t时段执行工序k所需的资源量,m为在t时段执行工序的总数,STi和Di分别为工序i的开始时间和持续时间。
(2)工序复杂度βi
用工序所在链路的复杂度来反映工序的复杂度[9]。用NP和NT分别表示工序紧前关系数和所在链路上的工序总数,工序i的复杂度可表示为:

(3)风险偏好水平ε
项目管理者根据项目价值评估和自身风险偏好,会选择不同的项目按期完工保证率,记风险偏好水平为ε,当链路包含的工序较多时,根据中心极限定理整个链路的工期近似服从正态分布。通过正态分布表可以确定在1-ε保证率下所对应的标准差倍数f1-ε,由此可计算出该风险水平下缓冲的调整系数:

其中,f95%为在95%保证率下对应的标准差倍数,查正态分布表有f95%=1.645。
由以上分析,综合工序资源紧张度、工序复杂度和管理者风险偏好水平,链路的缓冲估计为:

1.4 考虑开工柔性程度的缓冲计算方法
根据关键链项目管理理论[2],在适当的计划安排下,由中心极限定理,项目计划工期是服从正态分布的随机变量,其均值和方差分别对应着关键链上工序执行时间均值总和和方差总和,因此,在均值基础上加入一定的缓冲时间可以保证一定的完工保证率。
但是,这种结论必须满足两个条件:(1)各个工序执行时间是相互独立的随机因素;(2)项目执行过程中采取“接力”机制[15],即某一工作的紧前工作均已完成且资源满足要求时,马上开始该项工作。对于第二个条件,文献[16]认为许多项目难以满足,因为项目阶段里程碑所产生的级联效应使得前一工序提前完工时间不能为项目周期所利用,而延误却传递到最后一道工序。在项目实际执行过程中,当项目工序执行单位来自不同组织时,一般要求以合同形式规定开工时间,任何工序提前和延迟开工都是违约表现。因此,项目中不同工序开工柔性不同,它影响到对于“接力”机制条件的满足程度,这里的工序开工柔性是指允许工序开工时间波动的范围[11],波动范围越大,柔性越大。
杨立熙等[11]通过对剪贴法和根方差法的仿真模拟试验得出,工序开工柔性对剪贴法的完工保证率影响较小,对根方差法影响较大,且随着关键工序数的增大影响尤为明显。因此,对工序开工柔性小的项目在项目计划中应该适当增加缓冲,通过工序开工柔性程度修正因子对属性相关的缓冲设置方法进行修正:

其中ρ为工序执行时间不确定性程度修正因子,β为工序开工柔性程度修正因子,θ为在根方差法计算基础上加入的一固定值,目的是使完工保证率稳定在较高水平,同时与剪贴法相比可以缩短计划工期。
1.5 其他缓冲计算方法
除了上述缓冲估计方法外,Shou YY[13]等认为项目缓冲大小与工序工期不确定性和项目完工风险要求有关,通过对工序工期不确定性和项目安全进行等级划分,分别给出相应的缓冲换算系数;Zinov Y等[17]运用排队论理论,考虑在资源约束情况下,将资源视作服务台,工序当作顾客,为了不使服务台空闲,确定排队长度作为缓冲量的大小。
2 基于项目综合属性特征的缓冲计算方法研究
综合以上分析,除了50%法和排队论计算缓冲外,其他方法都是以工序持续时间不确定性为基础,考虑某一个或几个项目属性特征,如资源约束、项目管理者的风险偏好、工序的复杂程度以及项目工序开工柔性程度等来进行修正。但这些方法仅仅对某些方面进行调整,缺乏全面性,而且有的调整缺乏科学的量化方法,如开工柔性程度的缓冲计算方法中θ值的确定,就没有明确的量化依据。
在此基础以上,应综合考虑不同项目管理者的风险偏好α、资源约束β、工序的复杂程度χ以及项目工序开工柔性程度δ属性特征等情况,链路缓冲区计算方法为:


f1-ε为在风险水平(1-ε)保证率下所对应的标准差倍数;
f95%为在95%保证率下对应的标准差倍数,查正态表有f95%=1.645;
Rt为项目在t时段的资源供应限量,rkt为在t时段执行工序k所需资源量;
m为在t时段执行工序的总数,STi和Di分别为工序i的开始时间和持续时间;
NPi和NT分别表示工序所在链路上紧前关系数和链路上的工序总数;
δi表示工序i的开工柔性程度,柔性程度较小时取1.05,柔性较大时取1.0;
σi为工序i工期的标准差;
T∂i为在∂%的完工保证率下工序i的计划执行时间,公式取∂=95;
μi为第i个工序执行时间的均值。
在式(1)中,缓冲大小的五个影响因子可以分为两类,一类是对项目整体缓冲造成影响的因子,包括管理者的风险偏好α;另一类是对单个工序造成影响的因子,包括资源约束β、工序的复杂程度χ和项目工序开工柔性程度δ和工序持续时间不确定性σ。需要指出的是,综合属性缓冲计算方法是建立在根方差法思想的基础上,而根方差法的前提条件是:假定链路上工序时间参数的估计是相互独立的。但实际工作中链路上各工序可能受同种因素的影响而具有相关性,因此,对链路上工序时间参数μi和σi的准确合理估计是有效确定链路缓冲大小的基础。
3 结束语
缓冲区的大小直接决定着项目计划工期的确定和项目在计划进度内完成概率的高低。因此,对缓冲区进行合理计算和设置是关键链项目管理技术运用成功的关键。本论文在综合分析、比较目前各种项目缓冲区计算方法的基础上,提出了基于项目工序持续时间的不确定性、项目管理者的风险偏好、资源约束、工序的复杂程度以及项目工序开工柔性程度的综合属性特征缓冲区计算方法。但对于这种综合属性的全面性,是否存在其它缓冲影响因子,以及如何更加科学合理的确定这些因子对缓冲大小的影响等问题,需要作进一步深入研究。
[1]Leach L P.Critical Chain Project Management Improves Project Performance[J].Project Management Journal,1999,30(2).
[2]Herman Steyn.An Investigation into the Fundamentals of Critical Chain Project Scheduling[J].International Journal of Project Management,2000,19(6).
[3]Willy Herroelen,et al.Critical Chain Project Scheduling:Do Not Oversimplify[J].Project Management Journal,2002,(12).
[4]周雪,陈友玲.基于多项目关键链的ETO型企业计划管理方法[J].工业工程与管理,2008,(5).
[5]柴国荣,亓文国,洪兆富.基于资源共享的柔性关键链项目管理研究[J].统计与决策,2008(24).
[6]Tzvir,Robertb,Dovd.D.A Critical Look atCritical Chain Project Management[J].Project Management Journal,2003,34(4).
[7]Goldratt E M.Critical Chain[M].Great Barrington,Mass.USA: The North River Press Publishing Corporation,1997.
[8]Newbold R C.Project Management in the Fast Lane:Applying the Theory of Constraints[M].Boca Raton.Fla,USA:the St.Lucie Press, 1998.
[9]Tukel O,Rom W,Eksioglu S.An Investigation of Buffer Sizing Techniques in Critical Chain Scheduling[J].European Journal of Operational Research,2006,172(2).
[10]Herroel EN WS,Leus R.On the Merits and Pitfalls of Critical Chain Scheduling[J].Journal of Operations Management,2001,19(5).
[11]杨立熙,李世其,黄夏宝等.属性相关的关键链计划缓冲设置方法[J].工业工程与管理,2009,(1).
[12]马力,管在林,何敏等.基于关键链的自适应缓冲设置方法研究[J].华中科技大学学报(自然科学版),2008,36(11).
[13]Shou Y Y,Yao K T.Estimation of Project Buffers in Critical Chain Project Management[C].Proceedings of the 2000 IEEE International Conference on Management of Innovation and Technology,2000.
[14]褚春超.缓冲估计与关键链项目管理[J].计算机集成制造系统,2008,14(5).
[15]刘士新,宋健海,唐加福.资源受限项目调度中缓冲区的设定方法[J].系统工程学报,2006,21(4).
[16]杨雪松,吴昊.基于关键链方法的多项目管理[J].工业工程与管理,2005,10(2).
[17]Zinov Y,Radovil S K Y.A Quantitative Approach to Estimate the Size of the Time Buffer in the Theory of Constraints[J].International Journal of Production Economics,1998,55(2).
