价格上限下的高峰负荷电价效率比较研究
2010-03-11蔡建刚
叶 泽,蔡建刚,曹 花
(1.长沙理工大学经济与管理学院,湖南 长沙 410114;2.中南大学商学院,湖南 长沙 410083)
一、引言
从20世纪80年代末开始,全球范围的电力工业掀起了一场放松管制,进入竞争的改革浪潮。但是,放松管制并不意味着不需要管制,由于电力工业的特殊性以及其对整个国民经济发展的重要性,政府不但要对具有自然垄断性质的输、配电环节加强监管,而且还要对逐步放开的发电和售电环节进行价格核准与指导,从而防止电力企业垄断定价对消费者造成利益损失。
与一般商品不同,由于技术上的原因,电力商品无法储藏,这使得电力需求的波动不能依靠存货的调整来进行调节,而只能即产即销,实现电力供需的实时平衡。此外,在不同的时段,或者是一年中的不同季节,电力需求量存在明显的差异,这种差异对生产能力或者电力供应的成本是不同的。因此,电价的制定必须能体现出电力工业的这种特殊性。高峰负荷问题在那些不可储藏以及具有需求周期(一天、一周、一季度)波动的商品中比较突出[1]。所以,电力价格采取高峰负荷定价无论在技术还是在时间上都是合适的。
高峰负荷定价理论最早可以追溯到Houthakker(1951)关于长期边际成本定价的论述[2],Steiner(1957)对高峰负荷定价问题做了开拓性的工作[3],并经Boiteux(1960)、Williamson(1966)、Crew,Kleindorfer and Fernando(1976,1993)、Arellano and Serra(2007)、陈雯and谢武斌(2009)等人的发展[4-9],已经形成了一个完整的理论体系。然而,现有的文献并没有把价格上限和高峰负荷定价问题结合起来加以研究。文献[10-11]研究了高峰负荷定价与管制,但他们关注的是投资回报率管制(Rate of Return,ROR)。由于投资回报率管制具有“A-J效应”明显[12]、成本节约动力不足[13]、价格没有灵活性、信息需求量很大[14]等缺陷,被普遍认为是一种低激励的管制模式,已遭到社会各界的质疑。自英国人李特查尔德(Littlechild,1983)提出价格上限管制方法以来[15],价格上限管制已在全世界很多部门得到应用[14],并以英国电力工业最具代表性,它被认为是替代投资回报率管制的一种有效形式。目前,国内对电力价格管制模型的研究也大都是在价格上限模型(“RPI-X”管制模型)基础上进行的[16-18]。然而,价格上限管制在电力工业的应用依然是步履艰难,人们对价格上限的有效性提出了质疑。本文对不同价格上限形式下高峰负荷电价的效率进行了分析与比较,结论表明价格上限管制具有财务收支平衡效应,且在“RPI-X”管制下的高峰负荷电价收敛于拉姆塞价格,具有经济效率,这有利地支持了价格上限管制在电力工业的应用。
二、价格上限下的高峰负荷电价模型
(一)基本假设
假设整个电力需求分为高峰和低峰两个时期,Q1=f1(P1)和Q2=f2(P2)分别代表高峰时期和低峰时期的电力需求曲线,相应的逆需求函数为P1=P1(Q1)和P2=P2(Q2),高峰期和低峰期的需求是独立的,不存在交叉价格弹性,且它们在整个时期内持续的时间相等。
假设只发生两种成本①:c1、c2分别为高峰时期和低峰时期的边际电量成本(即边际运营成本),假定为常数;β为边际容量成本(即边际生产能力成本),与所需要的容量无关。
假设管制者(或政府)定价的目标是使社会福利(消费者剩余和生产者剩余之和)最大化,则我们可以将社会福利函数(W)表示如下:
(1)
式中,K表示最大生产能力或容量;δ为折现因子,0 <δ< 1②;t表示管制周期。
(二)不同价格上限形式下的高峰负荷定价模型
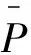
(2)
相对价格上限,即“RPI-X”管制,是指电力高峰期和低峰期的平均价格上涨率不能超过零售价格指数RPI(retail price index)的上涨率减去电力企业的生产率上涨率,用公式可以表示为:
(Pt-Pt-1)/Pt-1≤RPI-X或Pt≤Pt-1(1+RPI-X)③
(3)
式中,Pt表示本期的电力平均价格,Pt-1表示上一期的电力平均价格,RPI表示零售价格指数的上涨率,X表示电力企业生产率的上涨率。为了便于分析,假设RPI-X=0,即零售价格指数的上涨率等于电力企业生产率的上涨率。于是
Pt≤Pt-1
(4)
我们参考Cowan对价格上限模型的表述[20],引入拉氏物价指数(Laspeyres price index)和帕氏物价指数(Paasche price index)④,将式(2)和(4)分别转化成两种情况,即基于拉氏指数(LI)的价格上限(.1)和基于帕氏指数(PI)的价格上限(.2),表示如下:
(2.1)
(2.2)
(4.1)
(4.2)
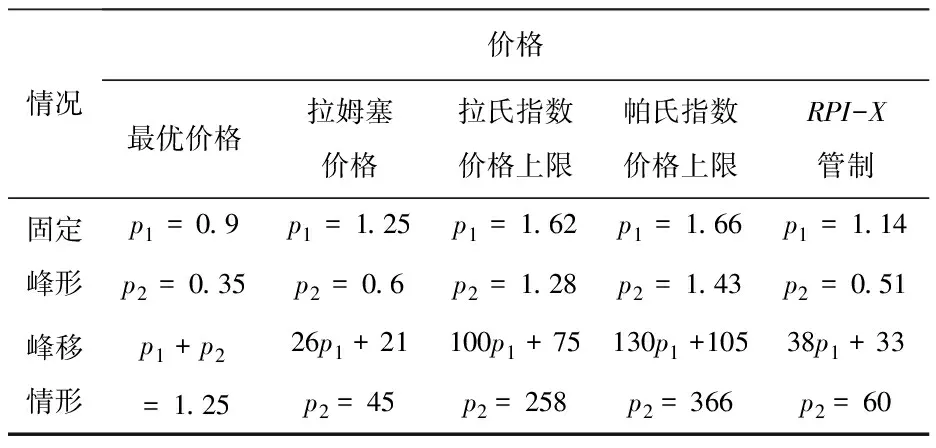
于是,定价问题就转化成为在上述四个条件下求社会福利最大化的问题,而该问题的关键是最优生产能力的确定。根据文献[14,21]的研究,最优生产能力取决于最大需求量,于是,K=max(Q1,Q2)。此外,高峰负荷定价存在“固定峰形”(Firm-peak)和“峰移情形”(Shifting-peak)两种情况[3,5],在固定峰形时,Q2 根据式(1)和(2.1)建立拉格朗日函数(引入拉格朗日乘数1),并对Qi,t求偏导,可以得到使社会福利最大化的一阶条件: (5) (6) (7) 利用库恩—塔克条件(Kuhn-Tucker Conditions)对式(5)、(6)、(7)分别加以整理可得: (8.1) (8.2) (8.3) 其中,ei为电力需求的价格弹性,ei=-[dQi/dPi]·[Pi/Qi] > 0;上标F表示“固定峰形”;上标S表示“峰移情形”。 根据式(1)和式(2.2)建立拉格朗日函数(引入拉格朗日乘数2),并对Qi,t求偏导,可得社会福利最大化的一阶条件: (9.1) (9.2) (9.3) 用同样的方法,我们可以得到式(4.1)条件下社会福利最大化的一阶条件: (10.1) (10.2) (10.3) 特别的,根据式(1)和(4.2)建立拉格朗日函数并对Qi,t求偏导得到的一阶条件与式(10.)几乎一样(唯一的差别在于拉格朗日乘数,3换成了4)。这意味着,在“RPI-X”管制下,拉氏物价指数和帕氏物价指数对高峰负荷电价所起的约束效应是相同的。 在不同价格上限形式下,我们得到了三组高峰负荷电价,即式(8.)、(9.)和(10.)。哪种管制形式下的高峰负荷电价更具经济效率,我们需要将这三组价格做一比较。 在福利经济学中,社会福利最大化是最具有普遍性的价值标准。霍特林指出,对所有东西都按照边际成本定价会使得福利达到最大化。也就是说,只要价格不等于边际成本,社会福利就会存在损失,资源就得不到最优配置。因此,最具经济效率的定价模式就是价格等于边际成本,任何偏离边际成本的定价都是缺乏效率的。然而,电力工业应其具有规模经济、范围经济以及固定成本大等特性,使得按边际成本定价会给企业带来亏损。因此,现实的定价方法是在确保电力企业收支平衡的前提下实现社会福利最大化,这便是拉姆塞定价。在高峰负荷定价下,拉姆塞价格可以表示如下⑤: (11.1) (11.2) (11.3) 此外,较基于拉氏指数的价格上限管制与“RPI-X”管制相比,基于帕氏指数的价格上限管制还存在一个高风险问题,这从式(2.2)可以清楚地看出。式(2.2)表明,价格上限约束规则依赖于与现行周期的价格和产量。换句话说,为了实现该约束,电力企业必须预测需求量,而电力需求具有不确定性,这样就增加了电力企业的风险。相反,在基于拉氏指数价格上限管制下,约束规则依赖于上一期的价格和产量,而上一期的价格和产量在本期来说都是已知的,这样就降低了风险。同样,由于拉氏物价指数和帕氏物价指数对“RPI-X”管制所起的效应是完全相同的,于是在“RPI-X”管制下,电力企业也可以根据上一期的价格和产量来实现约束,从而降低了风险。 表1 各种形式下的高峰负荷电价 图1 峰移情形下高低峰电价组合曲线 从图1可以更加直观地看到,在峰移情形时,“RPI-X”管制下的高峰负荷电价与拉姆塞价格最为接近,而绝对价格上限管制下的电价严重偏离了拉姆塞价格。由于拉姆塞价格是电力企业财务收支平衡约束下得出的价格,因此L2可以理解为是一条财务收支平衡线,任何低于L2的定价组合都将给电力企业造成亏损。相反,高于L2的定价组合会给电力企业带来利润。因此,“RPI-X”管制下的高峰负荷电价可能会给电力企业造成亏损。但是,不管何种形式的价格上限管制都有一定的财务收支平衡效应。如果仅从社会福利最大化的角度考虑(不考虑电力企业的财务收支平衡约束),“RPI-X”管制下的价格甚至优于拉姆塞价格,因为其与最优价格的偏差是最小的。也就是说,“RPI-X”管制下的电价更具有经济效率,电力商品的本期价格决定了下期的价格,这种价格调整使得电力企业可以在长期内优化价格水平,从而实现良性发展。此外,基于帕氏指数的价格上限管制下的高峰负荷电价偏离拉姆塞价格最大,其经济效率最差,这会导致消费者利益受损,而电力企业却获得高额垄断利润。这正是荷兰、英国等国不采用绝对价格上限,而采用“RPI-X”管制的原因所在。在电力工业,输配电网络的容量费用似乎是管制制度无可争议的一部分,而网络的容量也正是高峰负荷定价的关键。在荷兰,网络接入费用受“RPI-X”制度管制,“RPI-X”规定收费的水平,而费用准则(Tariff Code)则表明了高峰负荷结构留给网络运营商自主决定。在英国配电使用系统收费(Distribution-Use-of-System charges)中,也用“RPI-X”管制对高峰负荷定价进行了类似的规定。 合理的电价应是电价水平与电价结构的有机结合。价格上限针对的是电价水平问题,而高峰负荷属于电价结构问题,因此,研究价格上限下的高峰负荷电价问题不仅具有重大的理论价值,还具有实践意义。通过本文的研究,我们得到如下结论: 第一,价格上限管制具有财务收支平衡效应,但不同价格上限形式下高峰负荷电价的经济效率是不一样的,与绝对价格上限管制相比,“RPI-X”管制更具有优越性。在“RPI-X”管制条件下的高峰负荷电价趋向于拉姆塞价格,能在尽可能保障电力企业财务收支平衡的情况下最大化社会福利。同时,电力商品的本期价格决定了下期的价格,这种价格调整使得电力企业可以在长期内优化价格水平,从而实现良性发展。 第二,基于拉氏指数的价格上限管制是基于帕氏指数的价格上限管制与“RPI-X”管制的一种综合,随着折现因子δ取值的变化,基于拉氏指数的价格上限管制会完全变成基于帕氏指数的价格上限管制或者“RPI-X”管制。这意味着,在更一般的情况下,拉氏物价指数比帕氏物价指数更具适用性与现实意义。 第三,对于“RPI-X”管制来说,无论是采用拉氏物价指数还是帕氏物价指数,“RPI-X”管制所起的效应是完全相同的,这就缓解了理论界与实务界关于采用何种指数的激烈辩论,避免了某些计量上的争议,从而使“RPI-X”管制在电力价格管制实践中更具实用性。 [注释] ①在电力企业成本中有很大一部分是容量成本(即投资发电、输电、配电等的设备所产生的费用),由于其具有很强的专用性,无法回收,可以理解为是沉没成本。而沉没成本不应该影响企业的定价决策(详见平狄克,鲁宾费尔德.微观经济学(第六版)[M].北京:中国人民大学出版社,2006:215-217.),因此,在这里我们将其省略。 ②对折现因子δ我们可以作这样的理解:如果δ趋近于0,则表示该企业只重视眼前利益;如果δ趋近于1,则表示该企业注重长远利益。 ③理论界关于“PRI”的含义有不同的看法,有的将“PRI-1”看成是零售价格指数的上涨率(如杨君昌,2002),这里,我们将PRI直接理解为是零售价格指数的上涨率,其实质是一样的,并不影响研究的结论。 ④理论界关于拉氏物价指数和帕氏物价指数的“完美性”存在争议(详见平狄克,鲁宾费尔德.微观经济学(第六版)[M].北京:中国人民大学出版社,2006:98-102.),两个指数对生活成本的影响是不一样的。因此,基于这两个指数所构建的价格上限形式对电价的效率影响是有差别的。然而,以往的研究大都只考虑了拉氏物价指数(Cowan,1997;Brunekreeft,2003),并没有对帕氏物价指数多加阐述。 [参考文献] [1]Abrate G.Peak-load Pricing in the Electricity Market: Theory and Practice.Working Paper: University of Pavia,2004. [2]Houthakker H S.Electricity Tariffs in Theory and Practices[J].Economic Journal,1951,61(241). [3]Steiner P Q.Peak Loads and Efficient Pricing[J].Quarterly Journal of Economics,1957,71(4). [4]Boiteux M.Peak-Load Pricing[J].Journal of Business,1960,33(2). [5]Williamson O E.Peak-Load Pricing and Optimal Capacity under Indivisibility Constraints [J].American Economic Review,1966,56(4). [6]Crew M A,Kleindorfer P R.Peak-Load Pricing with a Diverse Technology[J].Bell Journal of Economics,1976,7(1). [7]Kleindorfer P R,Fernando C S.Peak-Load Pricing and Reliability Under Uncertainty[J].Journal of Regulatory Economics,1993,5(3). [8]Arellano M S,Serra P.Spatial Peak-load Pricing[J].Energy Economics,2007,29(2). [9]陈雯,谢武斌.电力市场高峰定价的数理模型建构[J].产业经济研究,2009,4(41). [10]Bailey E E,White L J.Reversals in Peak and Offpeak Prices[J].Bell Journal of Economics,1974,5(1). [11]Bergstrom T,MacKie-Mason J K.Some Simple Analytics of Peak-load Pricing[J].Rand Journal of Economics,1991,22(2). [12]Averch H,Johnson L.Behavior of the Firm under Regulatory Constraints[J].American Economic Review,1962,52(5). [13]Cremer H,Gasmi F,Grimaud A,Laffont J J.Universal Service: An Economic Perspective[J].Annals of Public and Cooperative Economics,2001,72(1). [14]Brunekreeft G.Regulation and Competition Policy in the Electricity Market: Economic Analysis and German Experience [M].Berlin: Nomos (Baden-Baden),2003. [15]Littlechild S.Regulation of British Telecommunications Profitability: A Report to the Secretary of State for Trade and Industry[M].London: Department of Industry,1983. [16]赵会茹,乞建勋,曾鸣等.输配电价格管制模型研究[J].中国电机工程学报,2003,23(10). [17]任晓红,任玉珑,张渝.中国电力产业价格管制模型[J].重庆大学学报(自然科学版),2005,28(2). [18]王成文,王绵斌,谭忠富等.适合我国输配电价的激励管制模型[J].中国电力,2008,41(2). [19]Acton J,Vogelsang I.Intruduction to the Symposium on Price-Cap Regulation[J].Rand Journal of Economics,1989,20(3). [20]Cowan S.Price-cap Regulation and Inefficiency in Relative Pricing[J],Journal of Regulato-ry Economics,1997,12(1). [21]Brunekreeft G.Price Capping and Peak-load Pricing in Network Industries.Working Paper: University of Freiburg,2000.三、对比分析及算例
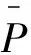
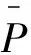
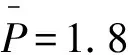

四、结论
