A New Chaotic Genetic Hybrid Algorithm and Its Applications in Mechanical Optimization Design
2010-03-09WANGZhongmin王仲民DAIYi戴怡
WANG Zhong-min(王仲民),DAI Yi(戴怡)
(College of Mechanical Engineering,Tianjin University of Technology and Education,Tianjin 300222,China)
Introduction
The optimization developed on the basis of mathematics is extensively used to find out the optimal solution of various engineering problems.As an important branch of science,it is much concerned and thus swiftly spread and applied in many engineering fields.In fact,lots of practical engineering problems can be analyzed and solved as a result of applying the optimization theory[1-2].The mechanical optimization design belongs to the group of complicated multidimensional nonlinear constrained optimization problem,rather than the usual convex programming problem.Therefore,seeking for a global optimum is always a huge difficulty in the world of engineering and applied mathematics[3].Traditional methods of optimization,which in most cases work through calculating gradient,are unable to overcome the nonlinearity and discontinuity of target functions.Moreover,they are easily trapped in local minimum.As a result,it is hardly satisfactory to optimize mechanical design by traditional optimization methods.Cylinder helix spring commonly used in all kinds of appliances,such as mechanics,meters,electrical equipment,transportation,common utensils and so on,are often ruptured in use.Hence,it is vital important to check the spring's shear stress.Additionally,the shear stress checking is a typical problem of the mechanical optimization design and needs to be further analyzed.
GA is a random search algorithm based on the mechanism of natural selection and heredity,which can guarantee the continuously evolution of population to approach the optimal solution.But,for the complicated nonlinear optimization problems,GA tends to lack the strong power to generate the optimal individual and leads the calculation to be slow when it gets close to the global optimized solution and even inevitably fall into local optimum[4].To solve this problem,some approaches which combine GA and problem-based heuristic search technique are developed,such as annealing GA ,immune GA,niche GA and chaos GA[4-5].Among them,it is worthwhile to pay attention to use chaos theory to improve GA.The chaos is a relatively common phenomenon in the nonlinear system.It appears to be chaotic,but has a fine inner structure and is characterized by randomness,ergodicity,regularity etc[6].The shortcomings of GA can be remedied by such merits of chaos above.
Combined the global situation of chaos ergodic optimization and inversion property of GA,this paper puts forward a new chaotic genetic hybrid algorithm(CGHA),which mainly consists of the chaos optimization“coarse-searching”and GA's“fine-searching”.Both processes work on repeatedly till the global optimum can be searched out according to a certain criterion.The calculation results for the check of spring shearing stress show that,compared with traditional penalty function algorithm,chaos-Powell and standard GA,CGHA is better in the global convergence and higher in the optimization efficiency.
1 MathematicalModelofSpring Shearing Stress Checking
1.1 Description of Mechanical Optimization Problem
The mathematical model of the mechanical optimization design problem can usually be described as a nonlinear constrained optimization problem[7].
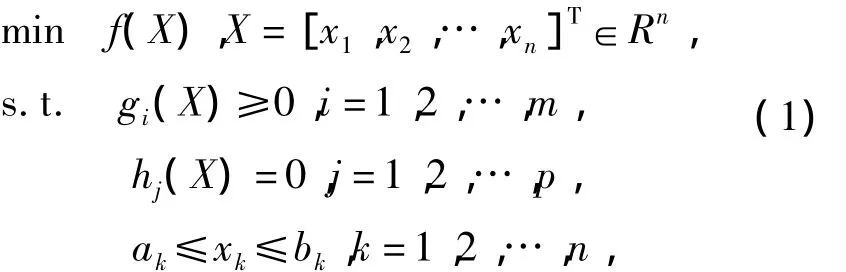
where f(X)is the target function,X=[x1,x2,…,xn]Tthe design variable,[ak,bk]the bound of the variable,gi(X)and hj(X)the inequality constraint and equality constraint,respectively.The set of the design variables satisfying all constrains constitutes a feasible field.And the solving mechanical optimization is just to find out the global minimum in this feasible field.
1.2 Optimization Design Model of Spring Shearing Stress Checking
Take a spring in a certain product as example.Its dimensional tolerance and technical requirements are d=(0.)mm,number of effective coils nw=5±0.25,inner diameter D1≥2.06 mm,outer diameter D2≤3.28 mm,free height H0=(9.)mm.The test requires its resistance to be 20.6 N to 25.5 N,when the spring is compressed to H2=4.2 mm.Though the spring has already been put into mass-production and its design formula and manufacturing technique are effective,there are still,about one third of them to be ruptured in use.The problem is being left either as the matter of design or that of manufacturing.From the view of design,the spring satisfying the conditions above needs to be checked.That is,the possibly potential maximum shear stress τmaxwould be greater than the allowable stress τ=1 750 N/mm2whether or not,when it deforms to H1=4.0 mm.The mathematical model of optimization can be found in Ref.[7-8].Apparently,it belongs to a nonlinear optimization problem that involves four variables and ten constraints.
2 Basic Idea of CGHA
2.1 Float Point Coding
The standard GA codes the optimized variable as binary.But,for the complex multidimensional optimization problems,the searching space increases rapidly,and the contradiction between the code length and solution precision is extraordinarily enhanced,and results into the decrease in GA's calculation efficiency.Furthermore,the Hamming cliff problem always accompanies with the binary coding[5].Hence,this paper adopts the method to code the optimized variable in float point directly,and it not only avoids the decoding process,but also effectively solves the contradiction between precision and code length.
2.2 Coarse-searching by Using Chaos Optimization
The convergence of GA depends on the selection of initial population closely.As there are a large number of individuals far away from the optimal solution in the initial population created randomly by standard GA,the efficiency of solving process is limited.On the contrary,the global coarse-searching by using the chaos ergodic property tends to have a better result.For this reason,it can be used to improve the quality of initial population and computational efficiency.
Consider Logistic mapping[9]

where Rkis the chaos variable,k=1,2,…,n,μ is the control parameter.When μ =4,Logistic mapping will be full mapping in[0,1],and then the whole system is completely in the state of chaos[9].Considered the searching probability of chaos sequence constructed by Eq.(2)is different in[0,1],according to Perron-Frobenius equation,the orbit probability density function is

In order to fully increase the ergodicity of chaos search,power function carrier was adopted in Ref.[10]to realize the chaos carrier,namely

where gmaxis the population's maximum number of evolutionary generations.Meanwhile,it adds the ith generated chaos variable xk,ito x*miwith a certain probability,as shown in Eq.(7),to obtain the mapping of chaos mutation individual in region[0,1].The degenerated operator α can be defined as where 0<c<d<1,0<u<1,v>1,Rkis the chaos variable generated by Eq.(2),is the chaos variable obtained after power function carrier.In[0,c],0<u<1,thus>Rk,it makes the point close to the left limitation in[0,c]move to the right.In[d,1],v>1,therefore<Rk,it causes the point near the right limitation to move to the left.The smaller the value of u is and the bigger the value of v is,the further the point will move.It is easy to prove that,when∈[0,1],will still have the ergodicity in[0,1].After this operation,the search homogeneity of chaos sequence in[0,1]is increased,thereby it enhances the optimization efficiency.Also,for the sake of mapping chaos variable from chaos space to that of relevant solution,should be changed as
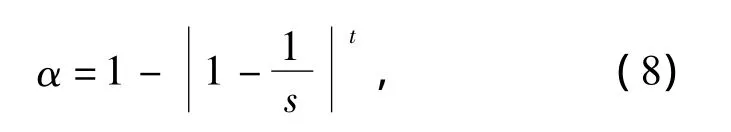

where akand bkare the bounds of design variable,i=1,2,…,n.For a fixed k,[xk,1,xk,2,…,xk,n]Trepresents a feasible solution in float point form.
2.3 Fine–searching by Using GA
On the basis of Ref.[11],this paper lays out a chaos degeneration mutation operator.It adopts the chaos variable directly to make ergodic search in solution space.The searching process goes on according to its own regulation.Therefore,it is more likely to gain a better optimized solution near the current optimal solution,thus overcomes the defect of a lower speed when the standard GA is reaching the global optimum.According to Logistic mapping shown in Eq.(2),it maps the population(xm1,xm2,…,xmn)in the mth generation's current solution interval(a,b)into the chaos variable region[0,1],and gets the chaos variable space vectorthen

where s is the number of iterations,t is an integer.Finally,the chaos individual mutation Ymiin region[0,1]is inversely mapped to the solution interval(a,b),then a mutation operation is finished,that is
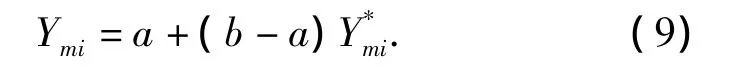
It can be seen from Eq.(7)and(8)that the degeneration mutation operator simulates the course of evolution as natural species.In the early stage,with a relatively high mutation ratio,a lot of evolutionary attempts contribute to the diversity of the population.In the later stage,when it begins to degenerate,the effect of the degeneration mutation operator become weaker and weaker as the evolutionary generation increases more and more,and therefore the effect of the cross operator intensifies and results in a conservative population.In this way,the combination of the cross and mutation operators can search finely in the local solution space.
3 Solving Process of CGHA
Each variable can be represented by decimal float point coding number.Then,set parameters,such as the scale of the population,cross probability,mutation probability and the times of chaos iteration.
Step 1Chaos initialization.Create the initial population.
Step 2Fitness calculation.Find out the fitness of each individual in the population according to the target function.
Step 3Selection and copy.Copy the individual by using competitive ways adapted in league matches according to the accommodation.
Step 4Cross.Carry out the cross operation in a certain cross probability.
Step 5Mutation.Complete the chaos degeneration operation and then yield the offspring according to a certain mutation probability by Eq.(7)and Eq.(8).
Step 6Judge the condition of convergence.If the number of maximum evolutionary generations or a satisfactory solution is reached,the whole optimization process ends.Otherwise,return to step 3.
4 Calculation and Analysis
The optimized results are shown in Table 1.Apparently,the target function decreases by 5.2%,compared with the traditional penalty function method.And,the solution is better than that obtained by using chaos-Powell hybrid algorithm mentioned in Ref.[8].It shows that CGHA has more powerful global convergence.The optimized result shows that the shear stress generated by the spring can reach a maximum of 2 134.5 N/mm2when the spring is working,and it is far greater than the allowable shear stress of 1 750 N/mm2.Because both parameters d=0.480 1 and nw=4.750 3 lay in the lower limit of tolerance,the effect of the tolerance on the spring's performance is relatively large.Thus,it can be considered that this condition arises due to technique problems.
Usually,the property of an algorithm can be reflected by three indexes,the times converging to the global optimal solution,which illustrates the global convergence of algorithm,the average number of evolution generation,which shows the speed of the convergence,and the mean value of optimal solution indicating the solution's quality[12].To further verify CGHA's exactness and availability,it is compared with standard GA.In both algorithms,set the population scale as 50,cross probability 0.6,mutation probability 0.15,times of chaos sequence iteration 400,and t=3.Both CGHA and GA operate 100 times randomly,and their calculation results are shown in Table 2.It can be seen that CGHA has the ability to converge into global optimization solution quickly,while the standard GA takes quite long time and it can not produce a satisfactory result.Moreover,CGHA has a 100% global convergence,which shows CGHA's validity sufficiently.

Table 1 Optimal results of maximum shear stress

Table 2 Performance comparison between GA and CGHA
5 Conclusions
This paper explores an approach that combines the chaos optimization and GA,then,proposes a new CGHA algorithm.Firstly,aiming to GA's defect,the initial populations are generated by adopting the chaos optimization in float point coding,the ergodicity of chaos variable is effectively improved by using the power function carrier,and thus the quality of the initial population and optimizing efficiency are enhanced.Secondly,a chaos degenerated mutation operator is designed.It overcomes the premature phenomenon existing in the standard GA in the evolution process.And thus,the trap of it efficaciously avoids being trapped into local optimum and increases the converging speed.Finally,the application of CGHA in shear stress checking of a cylinder helix spring shows its correctness and validity.The calculation results indicate that CGHA is superior to the traditional optimization methods and it is an effective algorithm to solve the problem of mechanical optimization design.
[1]CHEN Lun-jun.Mechanical optimization design based on genetic algorithm[M].Beijing:China Machine Press,2005.(in Chinese)
[2]YU Wen,LI Ren-hou.Study based on genetic algorithms for constrained optimization[J].Computer Science,2002,29(6):98-101.(in Chinese)
[3]FENG Chun.CHEN Yong. New global optimization method based on chaos and fractals[J].Chinese Journal of Mechanical Engineering,2004,40(2):96-101.(in Chinese)
[4]JI Gen-lin.Survey on genetic algorithm[J].Computer Applications and Software,2004,21(2):69 -73.(in Chinese)
[5]XUAN Guang-nan,CHENG Run-wei.Genetic algorithms and engineering optimization[M].Beijing:Tsinghua University Press,2004.(in Chinese)
[6]LIU He,HUANG Meng,LIU Gui-guo.A hybrid optimization method based on chaotic search and pattern search[J].Journal of East China University of Science and Technology(Natural Science Edition),2008,34(1):126-130.(in Chinese)
[7]WU Zao-han, WAN Yao-qing. Mechanicaloptimal design[M].Beijing:China Machine Press,1986.(in Chinese)
[8]HUANG Wen-pei,WANG Jin-nuo,YU Lan-feng.A hybrid algorithm combining powell method with chaos optimization method and its application to mechanical optimum design[J].Journal of Sichuan University(Engineering Science Edition),2001,33(5):31-34.(in Chinese)
[9]ZHANG Tong,WANG Hong-wei,WANG Zi-cai.Mutative scale chaos optimization algorithm and its application[J].Control and Decision,1999,14(3):285 - 288.(in Chinese)
[10]TANG Wei.Chaotic optimization method based on power function carrier and its applications[J].Control and Decision,2005,20(9):1043-1046.(in Chinese)
[11]LI Yao-hua,XU Le-jiang,HU Guo-xiang.Optimization method of slab location decision model based on chaos genetic algorithm[J].Journal of System Simulation,2005,17(11);2620-2624.(in Chinese)
[12]ZHANG Jing-dong,LIU Xiao-hui,DENG Fei-qi,et al.Intelligent integrate of genetic algorithm and chaotic optimization[J].Computer Engineering and Applications,2003,(16):17 -20.(in Chinese)
杂志排行
Defence Technology的其它文章
- Analysis on Velocity Characteristics of Cavitation Flow Around Hydrofoil
- Influence of Accelerated Aging on Detonation Performance of Explosives
- Research on Additional Loss of Guidance Optical Fiber
- An HLA/RTI Architecture Based on Multi-thread Processing
- A Fuzzy Adaptive Algorithm Based on“Current”Statistical Model for Maneuvering Target Tracking
- Quantitative Analysis of Components in OC-CS Sprays by High Performance Liquid Chromatography with Double Wavelength UV Detection
